Care este locul parametrului $p\in\mathbb{C}$, respectiv locul punctelor critice, dacă rădăcinile polinomului $f(z)=z^3+pz+q,\,z\in\mathbb{C}$ au de satisfăcut anumite condiţii de localizare?

Fiindcă monomul $z^2$ lipseşte, rădăcinile satisfac din start condiţia $z_1+z_2+z_3=0$. Să fixăm punctul $z_1$ undeva la distanţa 1 faţă de origine; altfel spus, $z_1$ este pe cercul unitate $\mathcal{C}:\,|z|=1$, putând fi exprimat în coordonate polare ca $z_1=\cos \alpha+i\sin \alpha=e^{i\alpha}$, pentru un unghi $\alpha$ dat. Locurile vizate mai sus depind de cum variază una dintre celelalte două rădăcini; aici considerăm cazul când $z_2$ are de parcurs cercul unitate:

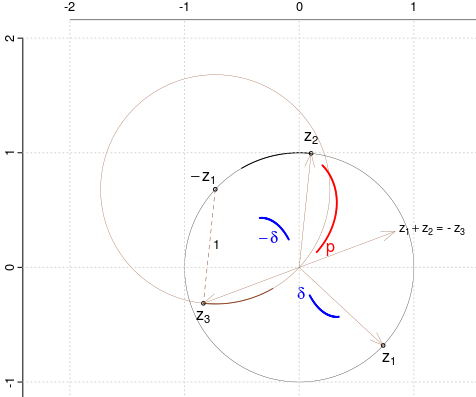
$z_1$ este fixat (aleatoriu) pe cercul unitate $\mathcal{C}$, iar $z_2=e^{i\theta},\,\theta\in[0,2\pi)$ se roteşte pe $\mathcal{C}$.

Însumând vectorii $z_1$ şi $z_2$ obţinem opusul vectorului $z_3$. Dar $z_3+z_1=-z_2$; deci $|z_3+z_1|=|z_2|=1$, adică $z_3$ va descrie cercul de centru $-z_1$ cu raza egală cu 1.

Avem de găsit (şi descris) locul punctelor $p=z_1z_2+z_1z_3+z_2z_3$ şi locul punctelor critice $\pm\delta=\pm\sqrt{-p/3}$ (v. [1]); de fapt, al doilea ar fi transformatul primului loc prin funcţia complexă sqrt().

Următorul program este tipic: se consideră un eşantion de puncte ale cercului unitate $\mathcal{C}$, dintre care se alege aleatoriu $z_1$; pentru fiecare punct $z_2$ din $\mathcal{C}$ se plotează punctele $z_2$ şi $z_3$ (formând pas cu pas cele două cercuri), precum şi punctele $p$ (cu roşu) şi $\pm\delta$ (cu albastru).

t <- seq(0, 2*pi, length=999)
C <- exp(1i*t)  # cercul unitate (un eşantion) 
z1 <- sample(C, 1)  # fixează aleatoriu z1
plot(z1, xlim=c(-3, 3), ylim=c(-3, 3), asp=1)
for(z2 in C) {  # z2 se roteşte pe cerc
  z3 <- -(z1 + z2)
  points(c(z2, z3), col="sienna4", pch='.')
  p <- z1*z2 + z1*z3 + z2*z3  # v. [1]
  delta <- sqrt(-p/3)  # punctele critice
  points(c(delta, -delta), col="blue")
  points(p, col="red")
}

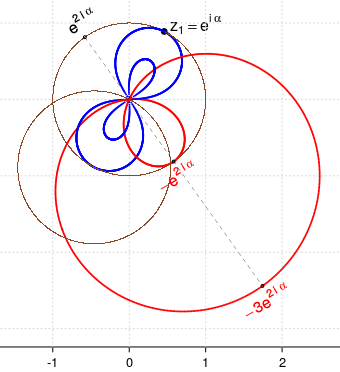
Plotând fiecare punct în parte, putem urmări cum se formează curbele respective (alternativa era de a genera punctele într-un vector - sau o altă structură de date - plotând numai în final, printr-o singură comandă, vectorul respectiv). Curba roşie ar fi locul punctelor $p$ - şi o vom nota prin $\mathcal{P}$ - iar cea albastră ar fi locul punctelor $\pm\delta$; pentru a le recunoaşte cumva (între diversele categorii de curbe), trebuie să încercăm să găsim ecuaţiile caracteristice.

Ştiind că $z_1+z_2+z_3=0,\,z_1=e^{i\alpha},\,z_2=e^{i\theta}$ unde $\alpha$ este fixat, iar $\theta$ parcurge $[0,2\pi)$ - putem scrie $p=z_1z_2+z_3(z_1+z_2)=-(z_1^2+z_2^2+z_1z_2)=-z_1^2\left( 1+\dfrac{z_2}{z_1}+\dfrac{z_2^2}{z_1^2}\right )$ şi obţinem exprimarea valorilor $p$ ca funcţie de parametrul $\theta$:

$\large p=p(\theta)=-e^{2i\alpha}\left(e^{2i(\theta-\alpha)}+e^{i(\theta-\alpha)}+1\right)\normalsize ,\,\theta\in[0,2\pi)\hskip5em (1)$

Rezultă întâi, că $|p|\le 3$ (ceea ce justifică alegerea limitelor pentru axe, în comanda plot() de mai sus), cu egalitate dacă $\theta=\alpha$; deci punctul de pe curba $\mathcal{P}$, care este cel mai depărtat de origine este $p_1=p(\alpha)=-3e^{2i\alpha}$. Din (1) avem şi $p_2=p(\alpha+\pi)=-e^{2i\alpha}\in\mathcal{P}$; pe figura de mai sus am marcat şi aceste puncte, iar imaginea sugerează că dreapta lor este axă de simetrie a curbei $\mathcal{P}$. Pentru a şi demonstra aceasta, ţinem seama de modul în care se poate determina simetricul unui punct faţă de o dreaptă care trece prin origine:

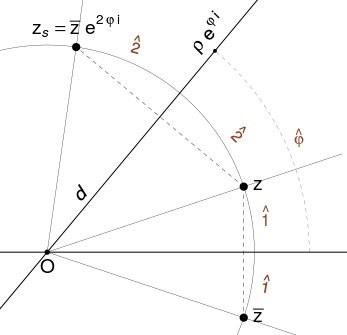
Dreapta $\mathit{d}\,$ trece prin origine şi este înclinată faţă de axa orizontală cu unghiul $\varphi$ (punctele ei sunt $\rho e^{\varphi i},\,\rho\in\mathbb{R}$).

Simetricul $z_{\mathit{s}}$ al unui punct oarecare $z$ faţă de $\mathit{d}\,$ poate fi obţinut rotind punctul $\overline z$ (conjugatul lui $z$) în jurul originii cu unghiul $2\varphi$ (arcul $\overline{z}zz_{\mathit{s}} = 2(\hat{1}+\hat{2})=2\hat{\varphi}$).

Prin urmare, $z_{\mathit{s}}=\overline{z}e^{2i\varphi}$ este simetricul lui $z$ faţă de $\mathit{d}\,$ (unde $\varphi$ este unghiul polar al dreptei $\mathit{d}$).

Simetricul unui punct oarecare $p=p(\theta)$ al curbei $\mathcal{P}$ faţă de dreapta $p_1p_2$ (a cărei direcţie este dată de $2\alpha$) este $p_{\mathit{s}}=\overline{p}e^{4i\alpha}$ şi se constată uşor (conjugând (1)) că $p_{\mathit{s}}=p(-\theta+2\alpha)$ - ceea ce înseamnă că $p_{\mathit{s}}\in\mathcal{P}$. Deci într-adevăr, $\mathcal{P}$ este simetrică faţă de dreapta care trece prin origine şi are direcţia $2\arg(z_1)$ (iar $p_1=-3e^{2i\alpha}$ şi $p_2=-e^{2i\alpha}$ sunt "vârfurile" celor două bucle roşii).

Dacă în (1) factorizăm prin $e^{i(\theta-\alpha)}$ - scriind $p(\theta)=-e^{2i\alpha}e^{i(\theta-\alpha)}(e^{i(\theta-\alpha)}+1+e^{-i(\theta-\alpha)})$ - şi apoi folosim relaţia $e^{it}+e^{-it}=2\cos t$, obţinem:

$p=p(\theta)=-e^{i(\theta+\alpha)}(2\cos(\theta-\alpha)+1),\,\theta\in[0,2\pi)\hskip5em (2)$

Exprimarea parametrică (2) evidenţiază şi raza polară $\rho=|2\cos(\theta-\alpha)+1|$ a punctelor $p\in\mathcal{P}$ şi unghiul polar corespunzător $\theta+\alpha$. Rezultă că $\mathcal{P}$ face parte din categoria curbelor cu ecuaţia polară generală $\rho=a\cos \varphi+b$ (denumită "melcul lui Pascal"); mai precis, $\mathcal{P}$ este o trisectoare ($a=2$ şi $b=1\lt a$; putem renota $\theta+\alpha$ cu $\theta$, încât $\varphi$ va fi $\theta-2\alpha$).

Ca idee, $\cos(\theta-\alpha)$ este cateta alăturată unghiului ($\theta-\alpha$) într-un triunghi dreptunghic cu ipotenuza de lungime 1; deci $2\cos(\theta-\alpha)$ ar fi lungimea bazei unui triunghi isoscel în care laturile egale au lungimea 1 şi fac cu baza unghiuri egale cu $\theta-\alpha$. "Citind" (2) în această manieră intuitivă, ajungem la o anumită construcţie geometrică:

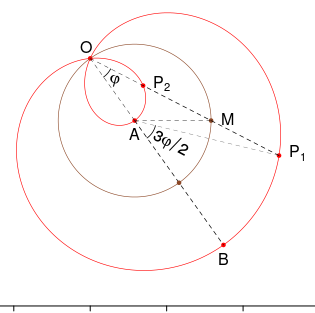
$P_1=p(\theta),\, P_2=p(\theta+\pi)\in\mathcal{P}$
şi $AO=AM=1$, cu $A=-e^{2i\alpha}$.

$\measuredangle P_1OA=\arg P_1-\arg A = (\theta+\alpha)-2\alpha=\theta-\alpha$, deci $OM=2\cos(\theta-\alpha)$ (din triunghiul isoscel MAO).

Ţinând cont de expresia razei polare pentru $P_1$ şi $P_2$, deducem că $MP_1=MP_2=1$ (avem OP = OM + MP = 2cos(θ-α) + MP, iar razele polare OP = |2cos(θ-α) + 1|).

În plus, $\measuredangle P_1OA=\varphi$ este a treia parte din dublul unghiului $\measuredangle P_1AB$ (de aici, denumirea de trisectoare).

În fond, am regăsit o construcţie cunoscută a punctelor trisectoarei: se consideră un cerc de rază r şi un punct fixat O al acestuia; se trasează drepte OM, M fiind un punct oarecare al cercului; pe OM se marchează punctele P₁ şi P₂ pentru care MP₁ = MP₂ = r; atunci P₁ şi P₂ parcurg împreună cele două bucle ale trisectoarei.

"Citirea" intuitivă redată mai sus (plecând de la interpretarea termenului $\cos(\theta-\alpha)$ drept catetă) are farmecul ei… Dar putem demonstra direct că M este mijlocul segmentului P₁P₂: este clar întâi, că P₁ şi P₂ sunt pe o aceeaşi rază polară (fiindcă argumentele lor diferă prin $\pi$); folosind acum (1), afixul mijlocului este $m=(p(\theta)+p(\theta+\pi))/2 = -e^{2i\alpha}(e^{2i(\theta-\alpha)}+1)=A-e^{2i\theta}$ - iar aceasta înseamnă că $m$ este situat pe cercul de centru $A(-e^{2i\alpha})$ şi de rază 1 (ştiind că ecuaţia cercului de centru z₀ şi de rază ρ este de forma z = z₀ + ρe^iφ, φ∈[0, 2π]). Rezultă că orice dreaptă dusă prin O taie $\mathcal{P}$ în puncte simetrice (şi la distanţă) 1 faţă de intersecţia acesteia cu cercul menţionat.

În urma acestor verificări - pentru ecuaţii, dar şi pentru proprietăţile principale ale curbei - rezultă că locul geometric $\mathcal{P}$ al valorilor parametrului complex $p$ al ecuaţiei $z^3+pz+q=0,z\in\mathbb{C}$, când o rădăcină este fixată şi o a doua este mobilă pe un acelaşi cerc cu centrul în origine, este o curbă trisectoare (cu axa de simetrie dată de dublul direcţiei rădăcinii fixe).

Transformând această trisectoare prin funcţia complexă sqrt() obţinem locul punctelor critice, $\pm\delta=\pm\sqrt{-p/3}$ (curba albastră din imaginea produsă prin programul redat mai sus); avem mai departe de căutat vreo clasificare şi de încercat o caracterizare a acestei curbe.