În [2] am produs în final structura 'jud.med', conţinând denumirile judeţelor împreună cu mediile corespunzătoare, pe linii ordonate descrescător după medie; lista începea cu Cluj 7.598, M.Bucureşti 7.592, Brăila 7.533, etc. şi se încheia cu Vaslui 6.296, Mehedinţi 6.270, ..., Giurgiu 5.945. Media judeţului rezulta ca valoarea medie a tuturor mediilor finale ale elevilor din judeţul respectiv…
Dar situaţia depinde considerabil şi de 'Mediu', cum am evidenţiat în [4]; prin urmare lista tocmai amintită este principial greşită - cel mai evident, în privinţa încadrării M.Bucureşti ("judeţ" care are numai 'URBAN', spre deosebire de judeţele propriu-zise). Pentru corectitudine era necesar să ţinem seama de proporţia celor două categorii de mediu, în fiecare judeţ; sau, cum vom proceda mai simplu aici - să tratăm separat cele două cazuri.

Recuperăm datele din fişierul "evna.RData" (constituit în [2]) şi selectăm numai coloanele pe care avem codul judeţului, indicaţia de mediu şi media finală:

load("evna.RData")
evna <- subset(evna, select=c('Cod_siiir', 'Mediu', 'Media'))
colnames(evna) <- c('jud', 'Mediu', 'media')

> str(evna)  # inspectează structura de date pe care am constituit-o
'data.frame':	163418 obs. of  3 variables:
 $ jud  : Factor w/ 42 levels "01","02","03",..: 40 40 40 40 40 40 40 40 40 40 ...
 $ Mediu: Factor w/ 2 levels "RURAL","URBAN": 2 2 2 2 2 2 2 2 2 2 ...
 $ media: Factor w/ 705 levels "","1","10","1.02",..: 135 313 261 467 419 367 ...

Înlocuim factorul 'media' cu valorile numerice corespunzătoare şi deasemenea, înlocuim codurile judeţelor cu denumirile acestora (preluate din structura 'evna.jMgf' pe care am constituit-o în [3]):

evna$media <- as.numeric(as.character(evna$media))
levels(evna$jud) <- levels(evna.jMgf$jud)

> str(evna)
'data.frame':	163418 obs. of  3 variables:
 $ jud  : Factor w/ 42 levels "Alba","Arad",..: 40 40 40 40 40 40 40 40 40 40 ...
 $ Mediu: Factor w/ 2 levels "RURAL","URBAN": 2 2 2 2 2 2 2 2 2 2 ...
 $ media: num  2.87 5.07 4.45 7 6.4 5.75 4.95 7.57 8.57 3.55 ...

Folosim acum funcţia aggregate(); prin 'FUN=mean' specificăm funcţia pentru calculul mediei şi anume - pentru fiecare grup de valori evna$media care ţin de un acelaşi judeţ şi mediu (conform formulei media ~ jud + Mediu, specificate la apel). Apoi, separăm cele două cazuri în structurile 'jud.rur' şi 'jud.urb' şi ordonăm în fiecare caz, descrescător după medie:

jud.mg <- aggregate(media ~ jud + Mediu, data=evna, FUN=mean)
tlst <- split(jud.mg, jud.mg$Mediu)
jud.rur <- tlst$RURAL  # coloana de 'Mediu' (a doua) devine inutilă 
jud.rur <- jud.rur[order(-jud.rur$media), c(-2)]  # ordonat după medii şi fără 'Mediu'
jud.urb <- tlst$URBAN
jud.urb <- jud.urb[order(-jud.urb$media), c(-2)]  # omite coloana 'Mediu'

Desigur că în loc să redăm ca atare valorile numerice rezultate astfel, putem prefera o sinteză grafică. Prin funcţia standard barplot() putem obţine o reprezentare cu bare pentru un vector sau o matrice; deci întâi, să transformăm 'jud.rur' (care este un "data frame") într-o matrice - şi anume, cu o singură coloană conţinând valorile din jud.rur$media şi având liniile denumite prin valorile din jud.rur$jud:

jud.rur.m <- matrix(jud.rur$media, ncol=1, byrow=T)
rownames(jud.rur.m) <- jud.rur$jud  # etichetează liniile matricei

De regulă, barele sunt etichetate cu denumirile coloanelor de date; transpunând matricea obţinută mai sus, obţinem 41 de coloane denumite prin numele judeţelor, fiecare coloană conţinând (drept singură valoare) media judeţului respectiv:

barplot(
    t(jud.rur.m),  # transpune (denumirile de linii devin numele coloanelor)
    ylim=c(5.25, 7),  # procentele pe RURAL sunt între 5.397 şi 6.91
    col="#EEEEEE",  # culoarea barelor (gri foarte deschis)
    las=2,  # pentru scriere de-a lungul barei (vertical)
    axes=F,  # renunţă la trasarea standard pentru axe
    cex.names=0.7,  # numele vor fi scrise cu dimensiune redusă
)
legend("top", bty="n", title="Evaluare Naţională 2015 - RURAL", legend=c(""), cex=1)
opar <- par(cex=0.7)
abline(h=seq(5.25, 7, by=0.25), col="lightgray", lty="dashed", lwd=1)
text(0, pos=2, seq(5.25,7,by=0.25), seq(5.25,7,by=0.25), srt=90)
par(opar)

Bineînţeles că am adăugat un titlu (folosind legend(), pentru a-l poziţiona înăuntrul graficului şi nu deasupra acestuia) şi linii orizontale de gradare (folosind funcţiile abline() şi text()) a axei verticale. Am obţinut scrierea denumirilor judeţelor chiar pe barele respective, fiindcă (pe lângă setarea las=2) am indicat o limită inferioară nenulă pentru gama valorilor axei verticale (altfel, pentru ylim=c(0, 7) denumirile respective ar fi fost scrise dedesubtul fiecărei bare):

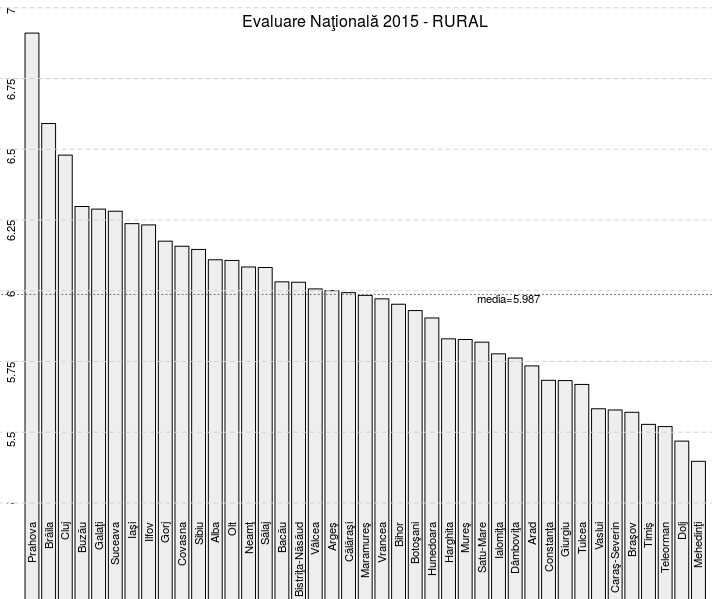
La sfârşit, am folosit iarăşi abline() pentru a adăuga pe grafic o linie orizontală punctată la gradaţia 5.987, corespunzătoare valorii medii a tuturor mediilor finale pentru 'RURAL'. Procedând absolut analog pentru 'jud.urb' - obţinem:

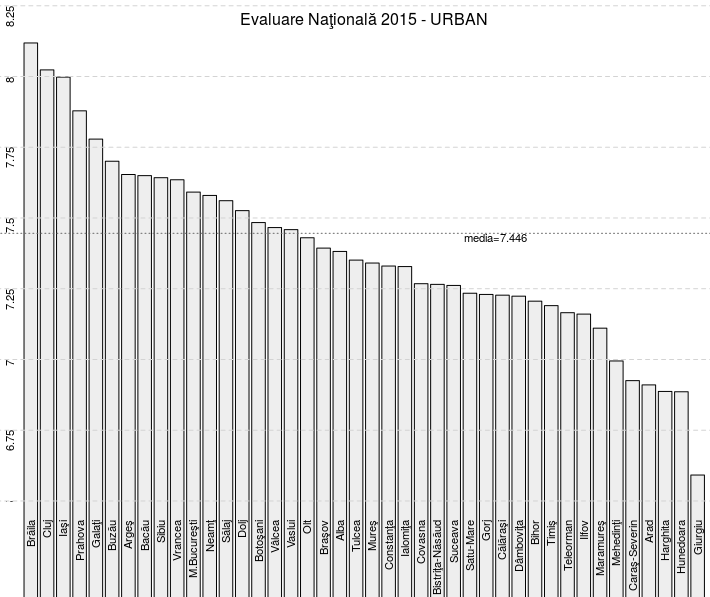
N-ar mai fi cazul să comparăm pe baza graficelor de mai sus, situaţiile pentru 'RURAL' şi 'URBAN' - am făcut-o deja anterior, de exemplu în [4].

Să observăm că acum (ţinând cont şi de 'Mediu', spre deosebire de [2]), 'M.Bucureşti' apare abia pe a 11-a poziţie, în lista ordonată după medii - pentru cazul 'URBAN' - tocmai redată grafic mai sus; avem desigur şi alte asemenea diferenţe poziţionale: de exemplu, Vaslui apare în prima jumătate a acestei liste (pe locul 17) - în timp ce în [2] (unde amestecam 'URBAN' şi 'RURAL') apărea la sfârşit.