"myProgram" pentru Sudoku, pas cu pas
[1] JavaScript Sudoku solver, Mihai Bazon
[2] Solving Every Sudoku Puzzle, Peter Norvig
[3] solveSudoku.R, din pachetul sudoku ( David Brahm, Greg Snow)
[4] hints for SOLVING SUDOKU, Angus Johnson
Pe de o parte, cei pasionaţi de jocuri—şi probleme—logice; pe de o altă parte, o seamă de programatori (sau/şi scriitori). Pasiunea pentru un joc logic sau altul este foarte răspândită şi este contagioasă; pasiunea pentru programare şi limbaje este rară şi nu ajunge la oricine. Toţi au o ambiţie nestăpânită, de a diseca şi a înţelege.
Pe unii îi atrage posibilitatea de a imagina „strategii” de joc, jargoane sofisticate şi raţionamente ingenioase; alţii „simplifică” şi modelează soluţionări mecanice, bazate pe teorii şi tehnici general aplicabile. Pentru unii timpul se măsoară în minute, pentru ceilalţi – în milisecunde; pentru câţi or fi (şi cine) – timpul nici nu contează.
Plăcerea de a raţiona
Începător fiind, încercăm a rezolva parţial un Sudoku pentru a ne da seama cât de cât, de problemă şi de subtilităţile jocului:
| 8 | 1 | |||||||
| 4 | 3 | |||||||
| 5 | ||||||||
| 7 | 8 | |||||||
| 1 | ||||||||
| 2 | 3 | |||||||
| 6 | 7 | 5 | ||||||
| 3 | 4 | |||||||
| 2 | 6 |
Avem o grilă cu 9 rânduri şi 9 coloane, grupate din trei în trei în 9 sub-grile (sau blocuri) de câte 9 celule. Trebuie completate celulele libere cu cifre 1..9, încât acestea să fie unice pe fiecare linie, coloană, sau bloc.
Să notăm celulele prin (hk), h fiind rangul de linie şi k, de coloană – iar blocurile prin B1..B9 (de la stânga spre dreapta grilei şi de sus în jos).
În B1 nu putem avea 2 decât în prima sau în a treia coloană – fiindcă 2 apare deja în coloana 2 (în cadrul blocului B4); bine – să zicem că în B1 am avea 2 într-una dintre cele trei celule din coloana 3 (poate fi oricare dintre acestea trei – fiindcă 2 nu apare încă, nicăieri pe primele 3 linii).
Atunci, pentru B7 rămâne posibilă numai prima coloană, pentru a înregistra pe 2 – dar nu în prima poziţie (ocupată deja de 6) şi nici în ultima poziţie (pe linia 9 avem deja un 2, în B8); rezultă că în B7 valoarea 2 trebuie înscrisă dedesubtul lui 6 (pe a 8-a linie a grilei), adică ar trebui să avem (81)=2 (dar nu-i sigur!).
Fiindcă acum 2 apare pe liniile 9 şi 8, în B9 vom avea 2 neapărat pe linia 7 – deci trebuie să înscriem (77)=2 (fiindcă (78) şi (79) sunt deja ocupate, de 7 şi 5); să observăm că deocamdată este posibil (77)=2, fiindcă pe coloana 7 încă nu există vreun 2 – în caz contrar deja putem concluziona că în B1, 2 nu se află în a treia coloană, cum presupusesem iniţial.
Raţionamentele de plasare mai departe a lui 2, în cele patru blocuri rămase (B2, B3, B5 şi B6) trebuie bifurcate prea mult – fiind de verificat multe ipoteze, care depind acum şi de alegerea liniei (care n-a contat mai sus) în care am plasat 2 pe a treia coloană din B1; deci mai inteligent ar fi să încheiem deocamdată cu 2 şi să încercăm să analizăm posibilităţile de plasare a lui 3 (de exemplu), în poziţia rezultată mai sus.
În B1, 3 nu poate figura după 5 (căci atunci, în B2 ar figura neapărat în prima linie, "8 3 1" – contradicţie cu faptul că 3 există deja, pe coloana 5); deci în B1, 3 trebuie pus pe prima linie (dar nu în coloana 3, pe care există deja). Ca urmare, în B2, 3 trebuie pus pe linia 3, fie în coloana 6, fie în coloana 8 – hai să zicem că punem (38)=3; atunci, în B8 3 va trebui pus neapărat în prima coloană (a 4-a din grilă) şi singura posibilitate este (74)=3. Rezultă că în B9, 3 trebuie pus în a 3-a linie (linia 9 a grilei) şi neapărat, (98)=3; dar atunci, în B6 ar trebui să avem neapărat pe prima coloană "8 1 3" – ceea ce vine în contradicţie cu faptul că 3 apare deja pe linia 6. Deci în B2, 3 nu poate apărea în a treia sa coloană, cum presupusesem; rămâne atunci că avem (36)=3.
La un moment dat vom ajunge să rejectăm şi ipoteza iniţială, că 2 ar figura în a 3-a coloană a lui B1; vom şti atunci, că în B1 avem 2 neapărat în prima coloană şi ar urma să „relansăm” raţionamente de genul celor redate mai sus…
Desigur, un jucător mai versat (v. [4]) ar putea avea o strategie superioară faţă de cea explorată mai sus, în care am angajat numai regula de bază: o valoare nu poate apărea de două ori pe o aceeaşi linie, coloană sau bloc.
De exemplu, în loc să ne grăbim să atacăm valoarea 2 pentru boxa B1, cum am făcut mai sus – era mai inteligent să observăm întâi un câmp liber care să fie cel mai convenabil de analizat: blocul B9 are fixate cel mai mare număr de valori (7, 5 şi 6), iar pe linia 6 avem deja înscrise 2 valori şi pe coloana 6 avem 3 valori – deci la intersecţia (67) rămân posibile numai (9-2-3-2=) două valori, anume 2 sau 9; fixăm una dintre acestea două (pe 2) şi dacă, raţionând mai departe, ajungem la o contradicţie – atunci va fi clar că (67) trebuie fixat pe cealaltă valoare (pe 9).
Cel mai puternic „jucător”?
Pentru poziţia Sudoku (cu 17 indicii) explorată mai sus, programele din [1] şi [3] – în javaScript şi respectiv în R – dau soluţia în mai puţin de o secundă, respectiv în 2-3 secunde (pe calculatorul meu, desigur):
vb@Home:~/21mai/sdk$ R -q
> library(sudoku)
> Z <- readSudoku("hardSu.txt")
> system.time(solveSudoku(Z))
2 3 7 8 4 1 5 6 9
1 8 6 7 9 5 2 4 3
5 9 4 3 2 6 7 1 8
3 1 5 6 7 4 8 9 2
4 6 9 5 8 2 1 3 7
7 2 8 1 3 9 4 5 6
6 4 2 9 1 8 3 7 5
8 5 3 4 6 7 9 2 1
9 7 1 2 5 3 6 8 4
user system elapsed
2.484 0.000 2.502
Iar prin [2] (în Python2) soluţia este chiar instantanee: 0.025 secunde; menţionăm că în [1] (după, între timp, anumite optimizări de cod) soluţia se obţine şi mai repede, în mai puţin de 10 milisecunde…
Este clar deocamdată, că un program „propriu” ("myProgram") onorabil, care să rezolve Sudoku, trebuie să dea răspunsul în nu mai mult de, foarte puţine, secunde. Pe de altă parte, cam tot aşa de clar este că nu atât timpul ne interesează, cât modul în care putem ajunge la soluţie.
Dar mai poate fi vorba astăzi, de un program propriu (care nu doar să imite, vreunul cunoscut)? Sunt multe demonstraţii (de obicei, implicite) că da – se poate formula îmbrăca şi un program propriu, care să depăşească sub diverse aspecte, imitaţia.
Diferenţe esenţiale şi… îmbinări
Într-un program pentru Sudoku, aspectul esenţial este (totuşi) structura de date concepută ca suport al rezolvării (fiind vorba nu numai de linii şi coloane, dar şi de blocuri şi în plus… de alocări); care ar fi diferenţele esenţiale între [1], [2] şi [3]?
În [2] şi [3] grila Sudoku este o matrice 9×9 (clasic!); în [1] este un vector cu 81 de întregi – dar… oarecum inconsecvent: diverse prelucrări (repetate) îl angajează convertind între indecşii 0..80 şi indicii 0..8 de linii şi coloane. În principiu, lucrul (direct) pe vectori simpli este mai eficient decât pe matrici bi- sau tri-dimensionale.
Regula de bază în Sudoku este aceasta: dacă pe câmpul S s-a plasat valoarea v=1..9, atunci v nu mai poate figura pe linia, coloana şi blocul 3×3 care conţin câmpul S.
Pentru a modela eficient această regulă, în [2] se instituie un dicţionar 'peers' care asociază fiecărui câmp S mulţimea celor 20 de câmpuri ale căror valori posibile sunt imediat afectate de valoarea pusă în S: cele 2×8 câmpuri diferite de S de pe linia şi coloana lui S şi cele 4 câmpuri rămase în blocul în care se află S. De exemplu,
print(peers['E3']) set(['F1', 'F2', 'F3', 'G3', 'E2', 'H3', 'I3', 'E1', 'C3', 'A3', 'E9', 'E8', 'B3', 'E5', 'E4', 'E7', 'E6', 'D2', 'D3', 'D1'])
unde A..I şi 1..9 desemnează liniile şi respectiv, coloanele grilei.
În schimb, în [3] se instituie un 'array' tridimensional cu 93 valori booleene, A[i,j,k]=TRUE însemnând că pe linia i şi coloana j s-a plasat valoarea k (modelând în fond, tratarea generală a constrângerilor binare asupra variabilelor – v. CSP).
Valorile posibile pentru fiecare câmp, pe parcursul rezolvării, sunt înregistrate ca şiruri de '0'..'9' în [2] (ştergând mereu câte o cifră, până ce se ajunge la soluţie), iar în [3] – comutând între TRUE şi FALSE valorile din A[i,j,k] (în final rămân exact 81 de valori TRUE). Investigarea posibilităţilor demarează în [2] identificând câmpul pentru care şirul înregistrat pentru valorile posibile are lungimea minimă, iar în [3] – identificând în tabloul A[,,k] câmpul cu cel mai mic număr de valori k=TRUE.
În [1] se evită alocările, "because the garbage collector costs time"; valorile posibile pentru un câmp nu sunt înregistrate într-un dicţionar sau 'array', ci sunt stabilite ad hoc, codificându-le pe biţi – apoi, deplasând spre dreapta întregul rezultat astfel, se extrage pe rând fiecare valoare posibilă şi se investighează consecinţele plasării acestei valori pe câmpul respectiv; câmpul de pe care demarează investigaţia curentă este cel pentru care, în momentul respectiv, întregul calculat pentru valorile posibile are cel mai mic număr de biţi 1.
Îmbinând de ici şi de colo, plecăm cam de la această idee „proprie”: într-un program R prealabil, constituim o listă în care intrării i=1..81 îi corespunde vectorul format din indecşii celor 20 de câmpuri care constituie, în notaţia din [2], "peers"[i]; vom opera pe un vector cu 81 de întregi, reprezentând fiecare (pe biţi) valorile posibile în momentul curent pe câmpul indicat de indexul întregului respectiv.
Căutăm să profităm de faptul că în R, operaţiile cu vectori sunt vectorizate – se aplică „în paralel” pe componentele vectorilor indicaţi (cu eventuală extindere, dacă lungimile diferă); de exemplu, c(1,2,3,4) + 1 ne va da vectorul c(2,3,4,5).
Ar mai fi ceva în plus, ţinând cu siguranţă de „ideile proprii”: ne încăpăţânăm ca de obicei, să examinăm minuţios şi să lămurim pe cât putem toate aspectele care apar pe parcursul dezvoltării „pas cu pas” a programului.
Tabele precalculate de indecşi
Să determinăm pentru fiecare câmp, indecşii celor 20 de câmpuri ale căror valori posibile vor fi imediat afectate de valoarea curentă înscrisă în acel câmp.
Indecşii câmpurilor din grila Sudoku (parcurgând-o de la stânga spre dreapta şi de sus în jos) sunt întregi 1..81 – deci valori de clasă 'integer', alocate pe câte 4 octeţi de memorie; dacă nu luăm măsurile necesare (convertind prin as.integer(), când este cazul), atunci pentru indecşii calculaţi mai jos, am obţine valori de tip 'numeric', pentru care se alocă de obicei câte 8 (sau 16) octeţi (aparent, diferenţa n-ar fi chiar mare; dar în principiu, operaţiile „pe biţi” necesită operanzi de tip 'integer'):
# idx_brc.R (tabele de indecşi ai câmpurilor grilei) i2rc <- function(i) c((i-1)%/%9+1, (i-1)%%9+1) # index 1..81 => (row_1..9, col_1..9) # indecşii câmpurilor din linia, coloana şi blocul care acoperă (exclusiv) câmpul indicat sq20 <- function(i) { rc <- i2rc(i) # Linia şi Coloana câmpului S de index 'integer' i=1..81 L <- (9*(rc[1]-1)+1):(9*rc[1]) # ':' produce implicit, 'integer' L <- L[L != i] # indecşii câmpurilor vecine pe Linie, cu S C <- seq(rc[2], by=9, length.out=9); C <- as.integer(C[C != i]) # indecşii vecinilor pe coloană cu S (ca 'integer'!) bij <- sapply(rc, function(v) ifelse(v<=3, 1L, ifelse(v<=6, 4L, 7L))) ul <- 9*(bij[1]-1) + bij[2] # index colţ stânga-sus al boxei B B <- c(ul, ul+1,ul+2,ul+9,ul+10,ul+11,ul+18,ul+19,ul+20) # indecşii pentru Boxă Bid <- as.integer(B[(B-i) %% 9 != 0 & abs(B-i) > 2]) # 4 câmpuri rămase în B c(L, C, Bid) } twe <- lapply(1:81, sq20)
i2rc() ne dă (ca şi în [1], dar ţinând cont că în R indecşii pleacă de la 1, nu de la 0) un vector având ca valori rangul 1..9 al liniei şi coloanei pe care se află câmpul de index indicat; precizăm că folosim această conversie numai în acest program prealabil (şi de fapt, programul s-ar putea formula şi fără a folosi i2rc(), observând că indicii cresc cu 1 pe linie şi cu 9 pe coloană; dar… nu mai rescriem).
Operatorul de secvenţiere ':' produce în mod implicit, un vector de tip 'integer' (aici 'L', conţinând indecşii câmpurilor de pe aceeaşi linie cu cel indicat); în schimb, seq() produce un vector 'numeric', încât (pentru coloanele 'C') am aplicat as.integer().
Pentru a viza cele 4 câmpuri rămase de adăugat, din boxa care conţine câmpul indicat – am folosit un mic truc: dacă 'ul' este indexul colţului stânga-sus al boxei, atunci indecşii celorlalte câmpuri ale acesteia se obţin adăugând consecutiv 1 pe linie ('ul+1' şi 'ul+2') şi incrementând cu 9 pentru fiecare linie următoare; dacă din cei 9 indecşi rezultaţi scădem indexul indicat (ceea ce în R este o operaţie „vectorizată”, B-i), atunci: diferenţele egale cu 1 sau cu 2, în valoare absolută, corespund celor două câmpuri vecine pe linie cu cel indicat (şi cei doi indecşi trebuie excluşi); iar diferenţele care sunt multiplu de 9 corespund celor două câmpuri vecine pe coloană, cu cel indicat (şi cei doi indecşi trebuie deasemenea, excluşi); pentru câmpul indicat iniţial, diferenţa este 0 – încât este exclus implicit şi acest index.
Prin programul redat mai sus obţinem un obiect de tip 'list', conţinând 81 de vectori, fiecare cu câte 20 de valori 'integer'; unul oarecare dintre aceştia se va putea accesa folosind operatorul de acces '[[':
> str(twe) # List of 81 # $ : int [1:20] 2 3 4 5 6 7 8 9 10 19 ... # $ : int [1:20] 1 3 4 5 6 7 8 9 11 20 ... ## etc. > twe[[25]] # indecşii asociaţi câmpului de index 25 # [1] 19 20 21 22 23 24 26 27 7 16 34 43 52 61 70 79 8 9 17 18
În twe[[i]], primii 8 indecşi indică vecinii de linie ai câmpului de index i, următorii 8 – vecinii de coloană; twe[[i]][17:20] indică vecinii de bloc, excluzând pe cei aflaţi chiar pe linia sau coloana câmpului de index i.
Pentru a putea viza direct toate cele 9 câmpuri dintr-o linie, coloană sau bloc – instituim şi liste de indecşi corespunzătoare acestora:
lsB <- lsR <- lsC <- vector("list", 9) b1 <- c(1:3, 10:12, 19:21) for(i in c(0L, 27L, 54L)) # fără sufixul 'L', în lsB rezultă 'num' (nu 'integer') for(j in 0:2) lsB[[i %/% 9 + 1 + j]] <- b1 + i + 3L*j # indecşii câmpurilor fiecărui bloc r1 <- 1:9 c1 <- seq(0L, by=9L, len=9) for(i in 1:9) { lsR[[i]] <- r1 + 9L*(i-1) # indecşii câmpurilor fiecărei linii lsC[[i]] <- c1 + i # indecşii câmpurilor fiecărei coloane } save(twe, lsB, lsR, lsC, file="idxBRC.rda")
Desigur, pe lângă fişierul ".rda" în care am salvat (în format specific pentru R) listele obţinute – puteam angaja de exemplu pachetul jsonlite, pentru a salva aceste liste şi în format JSON, putând apoi să le importăm direct şi într-un program javaScript, sau în Python, etc.
Încă un program R pentru Sudoku?
Poate că da, poate că nu… Măcar, îl vom dezvolta şi argumenta „pas cu pas” (în română!), încercând să promovăm în acest context şi limbajul R.
Pentru un mic exerciţiu de lămurire, să zicem că recuperăm din fişierul creat mai sus, lista celor câte 20 de indecşi şi introducem un vector 'Z' în care intenţionăm să menţinem valorile posibile pentru fiecare câmp, începând cu cele indicate iniţial:
# "mySudoku.R" load("idxBRC.rda") # listele 'twe', 'lsR', 'lsC', 'lsB' Z <- vector(mode = "integer", length = 81) sdk <- scan('hardS1.txt', what = integer(), quiet=TRUE) # datele iniţiale Z <- Z + sdk # mai jos vom constata că… ajungem astfel, pe un drum „greşit”!
Z este un vector cu 81 de întregi, cu valoarea iniţială 0; în 'sdk' am citit (prin scan()) grila Sudoku a cărei soluţionare se cere (folosind argumentul 'what' pentru a converti la 'integer' valorile citite) şi apoi, am însumat lui Z („în paralel”) datele respective.
Am presupus că grila iniţială este dată (în fişierul "hardS1.txt") în formatul cel mai obişnuit, marcând cu '0' (fără ghilimele) valorile care lipsesc (şi nu cu '.', sau cu '-', etc.) şi folosind spaţiul pentru a le separa (şi eventual '\n', pentru a separa liniile grilei).
O funcţie premergătoare care să convertească eventual la forma obişnuită este uşor de întocmit şi chiar nu este importantă, aici.
Important ar fi de verificat totuşi că grila dată este corectă (dacă o valoare deja se repetă, pe o linie, coloană sau bloc – atunci indiciile date sunt greşite); comanda necesară s-ar formula compact (cu lapply() şi ifelse() cu '%in%' – iar în final unlist()) astfel:
stopifnot("indiciile sunt greşite!" = unlist(lapply(1:81, function(i) ifelse(Z[i] != 0, !Z[i] %in% Z[twe[[i]]], TRUE))) )
interpretarea verbală fiind: dacă Z conţine o valoare nenulă care se regăseşte şi pe un câmp al lui Z dintre cele asociate câmpului de către twe, atunci programul va fi stopat şi se va afişa mesajul informativ specificat (înainte de "=") în stopifnot().
Pentru câmpurile rămase libere (cele pentru care în Z avem 0) este posibilă în acest moment, oricare valoare 1..9. Vom consemna aceste 9 valori pe biţi: pentru valoarea 1, setăm bitul de rang 0; pentru 2 – setăm bitul de rang 1; în general pentru v=1..9, setăm bitul de rang (v-1). Comutând pe 1 toţi cei 9 biţi inferiori, obţinem valoarea care acoperă toţi candidaţii, 1+2+22+...+28=511:
Z[Z == 0] <- 511 # 1 + 2 + 2^2 + ... + 2^8 = 2^9 - 1
Z[Z == 0] este un vector „paralel” cu Z în care avem TRUE sau FALSE după cum valorile din Z sunt nule, sau nu; la indecşii corespunzători valorilor TRUE se înscrie apoi 511.
Desigur… trebuie să fim atenţi (lucrul pe biţi este totdeauna, delicat). De exemplu, ce înseamnă că la un anumit moment ar rezulta în Z[i] valoarea 3?
Nu înseamnă că pe al i-lea câmp al grilei s-a fixat 3 – ci înseamnă că pentru acest câmp avem în momentul respectiv, doi candidaţi posibili, fie 1, fie 2 (fiindcă valoarea 3 acoperă biţii de rang 0 şi 1, corespunzători respectiv valorilor 1 şi 2).
Păi atunci… am început greşit: valoarea 3 citită din "hardS1.txt" şi pe care am înscris-o apoi ca atare (nemodificată) în Z, nu reprezintă „valorile posibile” 1 şi 2 – ci este chiar valoarea fixată deja în câmpul respectiv al grilei! Prin urmare, convenţia de consemnare pe biţi a valorilor posibile trebuie avută în vedere de la bun început.
Componentele de bază ale programului
Bineînţeles că nu ne grăbim (ca mai sus) să citim grila iniţială; preluarea datelor iniţiale este treaba programului „principal”, nu a celui care modelează rezolvarea.
# mysu.R load("idxBRC.rda") # listele de indecşi ai câmpurilor (twe, lsR, lsC, lsB) CRB <- c(lsC, lsR, lsB) # indecşii pentru coloane (1-9), linii (10-18), blocuri (19-27)
Intenţionăm să aplicăm chiar grilei iniţiale, un anumit raţionament de completare, angajând toate liniile, coloanele şi blocurile – de aceea am concatenat în CRB listele respective de indecşi; dar ordinea lor în CRB nu este lipsită de importanţă: pentru unele grile s-a dovedit preferabilă ordinea "RCB" (efectele finale rezultă ceva mai repede), pentru altele s-a dovedit suficientă restrângerea la "RC" (aplicarea pe blocuri nu mai produce nimic nou). Este drept însă, că pe unele grile (cele mai „grele”) raţionamentul respectiv se dovedeşte inutil – nu rezultă nicio simplificare.
Mai departe, prin "ICP" desemnăm generic „întregul candidaţilor posibili”, în care bitul de rang (v-1) arată candidatul v=1..9:
FIX <- as.integer(c(1, 2, 4, 8, 16, 32, 64, 128, 256)) # candidaţii posibili, 20..8
De exemplu: întregul candidaţilor 3 şi 9 pe un acelaşi loc, la un anumit moment,
va fi FIX[3] | FIX[9] = bitwOr(4, 256) = 260; iar which(bitwAnd(FIX, 260) > 0) va da indecşii din FIX ai candidaţilor acoperiţi (prin biţii 1) de ICP=260 – deci vectorul c(3, 9).
Unele reguli simple de „simplificare” vizează perechile de candidaţi; de exemplu, dacă pe o coloană avem două celule cu acelaşi ICP≡{3, 7}, atunci 3 şi 7 se pot elimina dintre candidaţii existenţi pe celelalte celule ale coloanei (analog, pentru linie sau bloc). Să determinăm din capul locului, perechile posibile de candidaţi distincţi:
FX2 <- setdiff(unique(as.vector(outer(FIX, FIX, bitwOr))), FIX)
outer() a aplicat bitwOr() pe oricare pereche neordonată de valori (distincte sau nu) din vectorul FIX; apoi, as.vector() liniarizează matricea rezultată, iar unique() furnizează numai valorile diferite două câte două din vectorul rezultat; în final, prin setdiff() se reţin numai valorile corespunzătoare la candidaţi distincţi.
Având FX2, putem depista uşor celulele cu câte 2 candidaţi: dacă Z este vectorul ICP-urilor tuturor celulelor grilei şi area este un element al listei CRB (deci conţine indecşii câmpurilor de pe o aceeaşi linie/coloană/bloc), atunci which(Z[area] %in% FX2) ne va da indecşii celulelor indicate în area care conţin exact doi candidaţi.
Următoarea funcţie returnează vectorul candidaţilor indicaţi prin biţii 1 dintr-un ICP primit ca argument:
splitICP <- function(icp) { # ICP ==> vectorul candidaţilor (codificaţi prin FIX) poss <- bitwAnd(icp, FIX) poss[poss > 0] } # ex.: splitICP(260) ==> [4 256]
Aplicând splitICP() elementelor referite prin vectorul Z, care diferă de valorile din FIX şi numărând de fiecare dată (prin length()) câte valori au rezultat, putem obţine un vector conţinând indecşii câmpurilor cu câte cel puţin doi candidaţi, ordonat (prin order()) după numărul de candidaţi:
restKand <- function(Z) { ## returnează vectorul indecşilor câmpurilor ne-fixate, W <- which(!Z %in% FIX) # ordonat după numărul de candidaţi pe loc ord <- sapply(1:length(W), function(i) length(splitICP(Z[W[i]]))) W[order(ord)] }
Desigur că pentru afişare, convertim candidaţii (văzuţi mai sus ca elemente din FIX) în şiruri simple de "1..9" (folosind toString() şi eliminând ', ' prin gsub()):
convICP <- function(icp) { # ICP ==> şirul candidaţilor 1..9 poss <- bitwAnd(icp, FIX) gsub(", ", "", toString(which(poss > 0))) } # exemplu: convICP(260) ==> "39" printKand <- function(Z) { # afişează cu 1..9, întregii ICP ai aspiranţilor mat <- sapply(Z, convICP) # converteşte fiecare ICP dim(mat) <- c(9, 9) # pentru a afişa vectorul obţinut, ca matrice 9×9 print.table(t(mat)) }
În R, matricele sunt „vectori de coloane” şi pentru a afişa liniile ei – am transpus matricea finală, prin t().
Se poate ghici după forma de redare, că iniţial, convICP() fusese încorporată în printKand(); le-am separat mai spre sfârşitul lucrurilor, având nevoie într-o anumită situaţie doar de convICP().
Avem acum toate elementele necesare pentru a începe să formulăm mecanismele intenţionate pentru soluţionarea unei grile Sudoku iniţiale.
Aspiranţi şi valori fixe deduse imediat
Următoarea funcţie primeşte ca argument un vector G (din clasa 'integer'), presupus a reprezenta o grilă Sudoku iniţială; valorile 0 corespund celulelor goale ale grilei, iar valorile nenule corespund acelor valori 1..9 (în număr de cel puţin 17) care au fost fixate din start pe anumite câmpuri (cum-necum – s-a demonstrat că trebuie fixate iniţial măcar 17 valori, pentru ca soluţia să fie unică).
Mai întâi, se constituie vectorul Z în care valorile 0 din G sunt înlocuite cu ICP=511, însemnând că pe câmpurile respective sunt posibile deocamdată toate valorile 1..9 (codificate prin FIX); valorile nenule v=1..9 sunt înlocuite prin elementul de rang v (anume, 2v-1) din vectorul FIX:
aspire <- function(G) { Z <- sapply(G, function(v) ifelse(v != 0, FIX[v], 511L)) stopifnot("indiciile sunt greşite!" = is_valid(Z)) return(cutKand(Z)) }
Obs. Probabil că este mai eficient de obţinut ICP-ul prin bitwShiftL(1, v-1), în loc de a-l accesa prin FIX[v]; dar vom avea de folosit FIX în diverse contexte (de exemplu, selectare prin operatorul %in%), încât pentru unitatea de formulare, preferăm FIX[v].
Vectorul Z rezultat astfel este apoi verificat, apelând is_valid(): dacă se descoperă că două valori fixate egale sunt „colegi” (adică se află pe o aceeaşi linie/coloană/bloc) atunci Z nu poate reprezenta o grilă Sudoku (iar la revenirea în aspire(), execuţia programului va fi stopată – „indiciile sunt greşite!”):
is_valid <- function(Z) { for(i in which(Z %in% FIX)) { # pentru valorile fixate v <- Z[i] tw <- twe[[i]] # indecşii colegilor celulei curente if(v %in% Z[tw]) return(FALSE) # v NU poate fi coleg cu el însuşi } return(TRUE) }
După validare, aspire() pasează vectorul Z funcţiei cutKand(); aceasta definitivează candidaţii pe fiecare celulă, plecând de la valorile fixate iniţial – anume, se anulează candidatura valorii fixate curent analizate, de pe câmpurile colegilor acesteia (folosind bitwAnd() şi bitwNot(), pentru a şterge bitul corespunzător valorii fixate respective, din ICP-urile colegilor acesteia).
Dacă, anulând astfel biţi 1 din ICP-uri – rezultă în final noi valori fixe (pentru care ICP-ul are un singur bit 1), atunci toate operaţiile menţionate se reiau (până când nu se mai obţin noi valori fixe valide):
cutKand <- function(Z) { nfix <- length(Z[Z %in% FIX]) repeat { # cât timp se deduc noi fixări pe locuri a unor candidaţi for(i in which(Z %in% FIX)) { # pentru valorile curent fixate v <- Z[i] tw <- twe[[i]] # indecşii colegilor celulei curente for(j in tw) # anulează candidatura lui v pe câmpurile colegilor if(bitwAnd(Z[j], v) > 0) Z[j] <- bitwAnd(Z[j], bitwNot(v)) } nfix1 <- length(Z[Z %in% FIX]) if(nfix1 == 81 | nfix1 == nfix) break nfix <- nfix1 } return(Z) }
Desigur, pentru cazul când Z provine prin aspire() direct din grila iniţială, cutKand() nu va descoperi noi valori fixe (decât în cazul neobişnuit când din start, s-ar fixa 8 valori pe o aceeaşi zonă din lista twe); însă vom putea aplica cutKand() şi pe vectori Z rezultaţi ulterior, prin diverse procedee de „simplificare” – iar în acest caz, definitivarea candidaţilor prin cutKand va putea conduce şi la noi fixări de valori (mergând eventual până la fixarea valorilor pe toate cele 81 de câmpuri).
O testare intermediară, pentru a vedea cum să continuăm
Ar fi momentul să testăm lucrurile, de exemplu pe grila Sudoku pe care ne-am exersat la început „plăcerea de a raţiona”. Salvăm deci fişierul constituit mai sus şi formulăm următorul mic program în care invocăm direct sau indirect, funcţiile aspire(), is_valid(), cutKand() şi printKand() din "mysu.R":
# test1.R source("mysu.R") grd <- c( 0, 0, 0, 8, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 3, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 0, 8, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 3, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 0, 7, 5, 0, 0, 3, 4, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 6, 0, 0 ) Z <- aspire(grd) printKand(Z)
Lansând prin source(), din consola R, obţinem tabelul valorilor fixate sau candidate, pe fiecare câmp al grilei (ceea ce este uşor de verificat):
vb@Home:~/21iun$ R -q > source("test1.R") [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 23479 34679 24679 8 24569 1 2579 2569 2679 [2,] 12789 16789 126789 5679 2569 25679 2579 4 3 [3,] 5 1346789 1246789 3679 2469 234679 279 12689 126789 [4,] 1349 134569 14569 1569 7 24569 8 23569 2469 [5,] 34789 3456789 456789 569 245689 245689 1 23569 24679 [6,] 14789 2 1456789 1569 3 45689 4579 569 4679 [7,] 6 1489 12489 139 189 389 2349 7 5 [8,] 12789 15789 3 4 15689 56789 29 1289 1289 [9,] 14789 145789 145789 2 1589 35789 6 1389 1489
Desigur, testăm programul nu doar pentru a constata că „merge”; se cuvine să examinăm cât de cât rezultatele produse, creându-ne şansa de a vedea cam cum ar trebui să continuăm dezvoltarea programului.
Putem observa că pe coloana 7, între cele 6 celule pe care se află câte 2, 3 sau 4 candidaţi, una singură conţine pe 3 (marcat cu albastru); prin urmare, putem fixa (77)=3 (şi cutKand() va elimina apoi candidatul 3 de pe linia 7 şi din blocul B9).
Fixarea lui 3 în celula (77) înseamnă şi retragerea candidaturilor iniţiale – 2, 4 şi 9 – de pe această celulă, ceea ce înseamnă că în blocul B9 rămâne o singură celulă pe care candidează 4 (marcat în tabel cu verde); rezultă deci o nouă fixare, (99)=4 (iar cutKand() va elimina pe 4 din celulele liniei 9 şi din cele ale coloanei 9).
Mai departe, consecinţa imediată este aceea că în blocul B6 rămâne o singură celulă care îl conţine drept candidat pe 4 (marcat cu verde în celula (67)) – prin urmare obţinem încă o valoare fixă, (67)=4.
O altă consecinţă imediată este eliminarea canditaturii lui 3 pe linia a 7-a (dat fiind că avem (77)=3) – încât pe coloana a 4-a rămâne un singur 3 (marcat cu roşu), deci ajungem să fixăm şi (38)=3.
Aceste observaţii arată că funcţia cutKand() va produce noi valori fixe, dacă o vom apela în urma unor „simplificări” care să modeleze raţionamente precum cele aplicate mai sus pe tabelul candidaţilor.
Reducerea candidaturilor
Cum am determina (dacă există) acea valoare care figurează drept „candidat” într-una singură dintre celulele unei zone (linie, coloană sau bloc) indicate?
Chestiunea este legată de frecvenţa apariţiei unor cazuri într-un set de date (de câte ori apare fiecare candidat, în fiecare celulă din zonă) – pentru care în R putem folosi de exemplu, table(). Dar ideea de bază este simplă şi o vom modela direct: constituim o matrice în care liniile corespund datelor, iar coloanele – cazurilor; la intersecţii „bifăm” cu 1 prezenţa cazurilor pe datele respective; în final, însumăm pe coloane – obţinând frecvenţele dorite.
De exemplu, pentru datele din coloana a 7-a a tabelului candidaţilor redat mai sus, am avea această matrice:
cand. 1 2 3 4 5 6 7 8 9 cell ----------------------------- 2579 1 1 1 1 1 2579 1 1 1 1 2 279 1 1 1 3 8 4 1 5 4579 1 1 1 1 6 2349 1 1 1 1 7 29 1 1 8 6 9 ----------------------- sum 5 1 2 3 4 6
Avem sum=1 pentru candidatul 3 (coloana 3), anume în celula a 7-a a coloanei.
Funcţia sole_in() (internă funcţiei simplify() redate mai jos) implementează aproape mot à mot procedeul descris mai sus, returnând un vector constituit din indexul celulei şi valoarea de fixat (pentru exemplul de mai sus, c(70, 4) – fiindcă FIX[3] este 4).
Funcţia cut_other() (internă şi aceasta, funcţiei simplify()) depistează – angajând vectorul FX2 – cazul când în zona indicată (linie/coloană/bloc) există două celule care conţin aceiaşi doi candidaţi (şi numai pe aceştia), retrăgându-i apoi de pe celelalte celule ale acelei zone.
Funcţia simplify() apelează cele două funcţii interne ei, pentru fiecare zonă din lista CRB şi de fiecare dată, apelează cutKand() (ceea ce determină eventual, fixarea pe grilă a unor noi valori):
simplify <- function(Z) { sole_in <- function(area) { # indecşii celor 9 câmpuri din linie/coloană/bloc knd <- Z[area] # întregii candidaţilor (ICP) pe câmpurile din 'area' if(any(knd == 511L) | all(knd %in% FIX)) return(NULL) # toate valorile au fost deja fixate în 'area', anterior m <- matrix(rep(0L, 81), nrow=9, byrow=TRUE) # 9 candidaţi × 9 locuri for(j in 1:9) { # analizează pe rând cei 9 ICP, knd[j] if(knd[j] %in% FIX) next # ignoră valorile deja fixate m[j, ] <- bitwAnd(knd[j], FIX) # candidaţi × locuri } m[m > 0] <- 1 # pentru a calcula numărul de candidaţi pe fiecare loc j <- which(colSums(m) == 1) if(length(j) == 1) # loc pe care este posibil un singur candidat return(c(area[match(1, m[, j])], FIX[j])) # index câmp, valoare de fixat return(NULL) } cut_other <- function(area) { # perechi identice de candidaţi w2 <- which(Z[area] %in% FX2) if(length(w2) == 2) { v <- Z[area[w2[1]]] if(Z[area[w2[2]]] == v) { idx <- setdiff(area, area[w2]) Z[idx] <<- bitwAnd(Z[idx], bitwNot(v)) # retrage de pe alte câmpuri } } } for(Q in CRB) { if(!is.null(ij <- sole_in(Q))) { Z[ij[1]] <- ij[2] Z <- cutKand(Z) } cut_other(Q) } Z <- cutKand(Z) return(Z) }
Subliniem că în cut_other(), pentru a „retrage de pe alte câmpuri” a trebuit să folosim '<<-' (şi nu '<-'), pentru că vectorul Z este extern funcţiei cut_other().
Următoarea funcţie, apelând repetat simplify(), fixează toate acele valori care se pot deduce urmând cele două reguli de reducere modelate mai sus:
fixgrid <- function(Z) { nfix <- length(Z[Z %in% FIX]); repeat { Z <- simplify(Z) nfix1 <- length(Z[Z %in% FIX]) if(nfix1 == nfix) break nfix <- nfix1 } return(Z) }
Aceste funcţii de „reducere” a candidaţilor, aşa cum au fost formulate mai sus, mizează în mod implicit pe corectitudinea valorilor fixate de la care se pleacă pentru a deduce noi valori fixe; ele se pot aplica grilei iniţiale – dar oare se pot folosi ele şi mai târziu, când ar fi de făcut încercări de fixare a unuia dintre candidaţii unei celule?
De exemplu, candidaţii posibili sunt 2 şi 9; încercăm pe 2 – dacă reducerile de mai sus ar invalida cumva această alegere, atunci ar rezulta fixarea lui 9; dar o asemenea invalidare este doar superficial gestionată, în formulările de mai sus.
Testări, constatări şi… corecturi
Cele două „reguli” modelate în sole_in() şi cut_other() sunt, în jargonul specific, "Hidden Single" şi "Naked Pairs" şi deşi simple, sunt foarte puternice – câtă vreme le iterăm pe toate zonele prin simplify() şi le aplicăm repetat prin fixgrid() – conducând pentru unele grile iniţiale, chiar la soluţionarea completă.
În următorul program de „testare” citim una sau alta dintre grilele iniţiale existente în fişiere precum "grid1.txt" şi îi aplicăm aspire() şi fixgrid() – afişând rezultatul, timpul de execuţie şi numărul de valori fixate (iniţial şi final):
# test2.R source("mysu.R") grd <- scan('grid1.txt', what = integer(), quiet=TRUE) print(matrix(grd, nrow=9, byrow=TRUE)) u <- system.time(Z <- fixgrid(aspire(grd))) printKand(Z) print.table(paste("fixate:",length(grd[grd > 0]), '=>', length(Z[Z %in% FIX]))) print(u)
În "grid1.txt" avem grila vizată deja anterior (în test1.R) şi… este un caz fericit:
> source("test2.R") [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 2 3 7 8 4 1 5 6 9 [2,] 1 8 6 7 9 5 2 4 3 [3,] 5 9 4 3 2 6 7 1 8 [4,] 3 1 5 6 7 4 8 9 2 [5,] 4 6 9 5 8 2 1 3 7 [6,] 7 2 8 1 3 9 4 5 6 [7,] 6 4 2 9 1 8 3 7 5 [8,] 8 5 3 4 6 7 9 2 1 [9,] 9 7 1 2 5 3 6 8 4 [1] fixate: 17 => 81 user system elapsed 0.055 0.000 0.055
Valorile din grila iniţială (omisă aici) sunt cele boldate, în număr de 17; se vede că în final s-au fixat chiar toate celelalte (81-17) valori, durata procesului fiind de ordinul zecilor de milisecunde. Este un caz fericit, soluţia rezultând direct, din grila iniţială, numai prin repetarea imbricată a celor două reguli menţionate.
Dar iată cum stau lucrurile pentru un caz mai dificil:
> source("test2.R") [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 236 36 9 1 268 7 4 68 5 [2,] 1467 567 1567 459 5689 489 678 3 2 [3,] 2467 8 2567 3 256 24 67 1 9 [4,] 17 2 17 8 4 39 39 5 6 [5,] 8 56 56 79 2379 239 39 4 1 [6,] 9 4 3 6 1 5 2 7 8 [7,] 237 37 278 457 3578 6 1 9 347 [8,] 5 1 678 479 3789 3489 678 2 347 [9,] 367 9 4 2 378 1 5 68 37 [1] fixate: 24 => 39
Plecând de la cele 24 de valori date iniţial, s-a reuşit fixarea a încă (doar) 15 valori.
Ca să ajungem la soluţie, ar trebui acum să începem să încercăm pe rând candidaţii rămaşi pe celelalte 42 de celule nefixate. Pe celula (12) – adică în Z[2] – avem candidaţii "36"; să-l fixăm pe 6 (prin ICP-ul corespunzător, din vectorul FIX) şi… să vedem ce se întâmplă dacă aplicăm apoi cutKand() şi fixgrid():
> Z[2] <- FIX[6] > W <- fixgrid(cutKand(Z)) > printKand(W) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 3 6 9 1 2 7 4 8 5 [2,] 4 7 1 59 59 8 6 3 2 [3,] 2 8 5 3 6 4 7 1 9 [4,] 1 2 7 8 4 39 39 5 6 [5,] 8 5 6 79 379 2 39 4 1 [6,] 9 4 3 6 1 5 2 7 8 [7,] □ 3 2 457 57 6 1 9 47 [8,] 5 1 8 479 379 39 □ 2 47 [9,] 7 9 4 2 8 1 5 6 3
Ne dăm seama că 6 nu este valoarea corectă, doar din faptul că afişând prin printKand() vedem şi celule goale ("□", pe care nu apare niciun candidat: (71) şi (87)) – dar corect ar fi fost ca deja cutKand() să fi sistat demersurile de fixare şi să semnaleze explicit că tentativa de a fixa 6 pe locul (12) trebuie respinsă.
Prin urmare, se impune să revenim în "mysu.R" şi să corectăm cumva, funcţia cutKand(); adăugăm de fapt o singură linie (dacă în urma anulării unor candidaturi, o celulă rămâne goală, atunci se încheie, returnând NULL) – dar aici redăm întreaga formulare:
cutKand <- function(Z) { nfix <- length(Z[Z %in% FIX]) repeat { # cât timp se deduc noi fixări pe locuri a unor candidaţi for(i in which(Z %in% FIX)) { # pentru valorile curent fixate v <- Z[i] tw <- twe[[i]] # indecşii colegilor celulei curente for(j in tw) # anulează candidatura lui v pe câmpurile colegilor if(bitwAnd(Z[j], v) > 0) Z[j] <- bitwAnd(Z[j], bitwNot(v)) if(0 %in% Z) # sistează, dacă rezultă colegi identici! return(NULL) } nfix1 <- length(Z[Z %in% FIX]) if(nfix1 == 81 | nfix1 == nfix) break nfix <- nfix1 } return(Z) }
Acum, dacă reluăm "test2.R" şi încercăm iarăşi să fixăm 6 în celula (12) - obţinem NULL, în loc de tabelul cu celule goale rezultat anterior. Deci 6 este greşit; să probăm că varianta cealaltă, 3 este cea care trebuie fixată:
> Z[2] <- FIX[3] > W <- fixgrid(cutKand(Z)) > printKand(W) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 26 3 9 1 268 7 4 68 5 [2,] 1467 56 1567 459 5689 489 678 3 2 [3,] 2467 8 2567 3 256 24 67 1 9 [4,] 17 2 17 8 4 39 39 5 6 [5,] 8 56 56 79 2379 239 39 4 1 [6,] 9 4 3 6 1 5 2 7 8 [7,] 23 7 28 45 358 6 1 9 34 [8,] 5 1 68 479 3789 3489 678 2 347 [9,] 36 9 4 2 378 1 5 68 37 > print(length(W[W %in% FIX])) [1] 41
După ce am fixat direct Z[2]=FIX[3], s-a mai dedus o singură valoare corectă (7, în celula (72)) şi acum avem fixate 41 de valori. Mai departe să vedem, iarăşi prin încercare, care este cel bun dintre candidaţii "26" de pe celula (11):
> W[1] <- FIX[2] > w1 <- fixgrid(cutKand(W)) > printKand(w1) NULL # '2' se respinge; deci '6' este varianta corectă > W[1] <- FIX[6] > w1 <- fixgrid(cutKand(W)) > printKand(w1) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 6 3 9 1 2 7 4 8 5 [2,] 4 5 1 9 6 8 7 3 2 [3,] 7 8 2 3 5 4 6 1 9 [4,] 1 2 7 8 4 3 9 5 6 [5,] 8 6 5 7 9 2 3 4 1 [6,] 9 4 3 6 1 5 2 7 8 [7,] 2 7 8 5 3 6 1 9 4 [8,] 5 1 6 4 7 9 8 2 3 [9,] 3 9 4 2 8 1 5 6 7
Constatăm că varianta corectă este '6', iar după fixarea directă şi a acestei valori s-a ajuns – aplicând repetat cele două reguli menţionate – la soluţionarea întregii grile.
Aparenţe… şi soluţii interactive
Am putea crede că procedeul ilustrat mai sus prin "test2.R" permite soluţionarea (treptată, într-adevăr) pentru orice grilă G: mai întâi, prin fixgrid(aspire(G)) constituim tabelul candidaţilor; apoi, alegem o celulă pe care avem mai puţini candidaţi şi îi încercăm pe rând, prin fixare directă (Z[index_celulă] <- candidat) – dacă apoi, fixgrid(cutKand(Z)) returnează NULL, atunci ştim că acel candidat nu este bun şi repetăm pentru următorul candidat… Mai sus am soluţionat astfel (şi numai în două sau trei „trepte”) chiar şi „un caz mai dificil” – dar este totuşi doar o întâmplare.
Să considerăm cazul grilei denumite "Harder" în [1]:
> source("test2.R") [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 125 12567 3 9 1245 14567 2478 2458 2457 [2,] 4 12579 12579 1257 8 157 279 3 6 [3,] 259 25679 8 234567 2345 34567 1 2459 24579 [4,] 1259 4 1259 158 6 1589 289 7 3 [5,] 8 235679 25679 3457 3459 34579 2469 1 2459 [6,] 1359 135679 15679 134578 13459 2 4689 4589 459 [7,] 12359 12359 4 1235 7 1359 239 6 8 [8,] 6 123589 1259 123458 123459 134589 23479 249 12479 [9,] 7 12389 129 123468 12349 134689 5 249 1249 [1] fixate: 22 => 22
fixgrid(aspire(G)) nu a fixat nicio valoare, faţă de cele 22 date iniţial. Pe celula (11) trebuie fixat unul dintre candidaţii "125"; să încercăm pentru "1", pe o copie a lui Z:
> W <- Z > W[1] <- FIX[1] > w1 <- fixgrid(cutKand(W)) > printKand(w1) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 1 2567 3 9 245 4567 2478 2458 2457 [2,] 4 2579 2579 1257 8 157 279 3 6 [3,] 259 25679 8 234567 2345 34567 1 2459 24579 [4,] 259 4 1259 158 6 1589 289 7 3 [5,] 8 235679 25679 3457 3459 34579 2469 1 2459 [6,] 359 135679 15679 134578 13459 2 4689 4589 459 [7,] 2359 12359 4 1235 7 1359 239 6 8 [8,] 6 123589 1259 123458 123459 134589 23479 249 12479 [9,] 7 12389 129 123468 12349 134689 5 249 1249
fixgrid(cutKand(W)) nu a produs NULL (şi nici vreo nouă valoare fixă, afară de "1" pe care-l fixasem direct); ar trebui să deducem că "1" este valoarea corectă pe câmpul (11)? NU! – fiindcă se obţine un rezultat similar (nu rezultă NULL) şi dacă încercăm în loc de "1", pe "2" sau pe "5"…
Cum să deducem atunci, unica variantă corectă dintre cele trei?
S-ar putea să existe, un set de „reguli” care adăugate celor două (cele mai simple) instrumentate în funcţia noastră simplify(), să rezolve şi excepţiile evidenţiate mai sus (când nu putem decide aplicând regulile, care este varianta corectă); dar cel mai probabil, pentru setul respectiv de noi reguli (care mai sunt şi dificil de implementat) tot se vor găsi excepţii…
Să operăm mai departe în consola R în care am rulat test2.R şi după W[1] <- FIX[1] am obţinut tabelul redat mai sus; fiindcă "1" nu a fost invalidat, îl putem considera măcar temporar ca fiind varianta corectă. Atunci să continuăm, alegând de exemplu celula (15) şi dintre cei trei candidaţi "245", să fixăm pe "2" (W[5] <- FIX[2]); ca şi în cazul anterior când fixasem pe "1", obţinem nu NULL, ci un nou tabel de candidaţi; deci măcar temporar este valabilă şi această a doua fixare de valoare.
Redăm sintetic operaţiile desfăşurate interactiv, începând de la fixarea lui "1" pe poziţia (11) din tabelul de candidaţi redat mai sus, a lui "2" pe poziţia (15) din tabelul de candidaţi rezultat prin precedenta fixare, ş.a.m.d. până ce obţinem şi anumite invalidări NULL:
index candidaţi fixare rezultat 1 125 1 nou tabel; pe (15) avem "245" 5 245 2 pe (18) avem "48" 8 48 4 la indexul 16: "29" 16 29 2 NULL ("2" cade; fixăm pe "9") 16 29 9 nou tabel; la indexul 11: "27" 11 27 2 NULL ("2" cade; fixăm pe "7") 11 27 7 nou tabel; la indexul 13: "15" 13 15 1 la indexul 32: "34" 32 34 3 NULL ("3" cade; fixăm pe "4") 32 34 4 NULL (cade şi "4")
Constatăm că niciunul dintre cei doi candidaţi "34" nu poate sta (pe baza lanţului de fixări anterioare) pe celula de index 32 (deci la indexul 32 trebuie să înscriem înapoi "34"); rezultă că "1" pe care-l pusesem la indexul 13 este invalid – deci îl înlocuim cu "5" şi reluăm; dacă mai departe, va rezulta o situaţie similară cu aceea evidenţiată pentru "34", atunci nici "5" nu poate sta la indexul 13 şi mergând înapoi pe lanţul de fixări, rezultă că "4" fixat la indexul 8 nu-i bun, deci îl înlocuim cu celălalt candidat "8" şi reluăm, ş.a.m.d.
În concluzie, dacă e să rezolvăm orice grilă Sudoku, atunci nu sunt suficiente proceduri de reducere precum cele pe care le avem deja în simplify() şi cam suntem condamnaţi să instrumentăm şi un mecanism de „căutare cu revenire” (backtracking), cum am ilustrat interactiv mai sus.
Programe principale
mysu.R conţine deja componentele de bază pentru rezolvarea unei grile Sudoku şi pentru a obţine soluţia, trebuie doar să le îmbinăm cumva, implicând eventual şi un mecanism de "backtracking".
Mediul R oferă o consolă pentru lucrul interactiv (folosită şi în experimentul redat mai sus) şi permite reconstituirea sesiunii de lucru anterioare; în loc să adăugăm în mysu.R şi funcţia cuvenită pentru "backtracking", preferăm să închidem acum fişierul mysu.R şi să formulăm câte un mecanism de rezolvare a grilei, în câte un program separat.
Fiindcă într-adevăr, putem vorbi de mai multe „mecanisme de rezolvare”, meritând să fie investigate prin câte un program separat; de exemplu, putem formula numai tabelul de bază al candidaţilor – aplicând fixgrid(aspire()) grilei iniţiale – şi mai departe să folosim doar backtracking, uitând complet de simplify(); sau dimpotrivă, în cursul încercărilor din backtracking să angajăm cumva şi fixgrid(cutKand()).
Am avea deci câte un „program principal”, care după ce include mysu.R, va citi cumva o grilă iniţială, va formula tabelul de bază al candidaţilor pe celulele rămase goale şi apoi va rezolva grila într-un fel sau altul, angajând unele sau altele dintre cele prevăzute în mysu.R.
Un „program principal” cu fixare temporară de candidaţi
În primul program, implementăm mecanismul de backtracking fără a reduce pe parcurs, tabelul de candidaţi iniţial:
# solve1.R (backtracking pe tabelul de bază al candidaţilor) source("mysu.R") grd <- scan('grid3.txt', what = integer(), quiet=TRUE) # ; print(grd) Z <- fixgrid(aspire(grd)) # tabelul de bază al candidaţilor Rest <- which(!Z %in% FIX) ## indecşii celulelor goale, în ordinea din grilă # Rest <- restKand(Z) ## ordonează indecşii celulelor după numărul de candidaţi lKan <- lapply(Rest, # index celulă goală ==> vectorul candidaţilor (ca ICP-uri) function(v) splitICP(Z[v])) Result <- NULL # aici vom salva soluţia back <- 0 # intenţionăm să contorizăm revenirile reshat <- function(Z, ref = 1) { # 'ref' referă elementele vectorului 'Rest' # cat(ref, '\n') # dacă vrem să evidenţiem referirile pe celule if(ref > length(Rest)) { # s-au investigat toate celulele "goale" Result <<- Z # exportă soluţia return(TRUE) # nu avem de căutat o a doua soluţie } idx <- Rest[ref] for(knd in lKan[[ref]]) { # încearcă pe rând candidaţii celulei curente if(knd %in% Z[twe[[idx]]]) # ignoră, dacă există deja în zona din 'twe' next Z[idx] <- knd # 'knd' este măcar temporar, un candidat "bun" if(reshat(Z, ref + 1)) # avansează la următoarea celulă din 'Rest' şi repetă return(TRUE) } # când un candidat temporar "bun" se dovedeşte ulterior a fi invalid, # se revine din aproape în aproape la celulele precedente, reluând căutarea back <<- back + 1 # contorizează revenirile return(FALSE) } u <- system.time(reshat(Z)) cat("Tabelul de bază al candidaţilor:\n") printKand(Z) cat("\nSoluţia finală (prin backtracking pe secvenţa celulelor cu candidaţi):\n") printKand(Result) cat("\n clues:", length(grd[grd > 0]), "; fixed before 'backtracking':", 81 - length(Rest), "\ntimp (backtracking):", u["elapsed"], "sec.", "\ntotal reveniri în secvenţa celulelor:", back, '\n')
Am denumit reshat() funcţia care implementează "backtracking" – de la решать ("a rezolva", în rusă); nu puteam folosi denumirea frecventă "solve", fiindcă solve() este în R o funcţie care permite rezolvarea unui sistem de ecuaţii liniare.
După ce am obţinut în Z tabelul de bază al candidaţilor, am constituit vectorul Rest în care am plasat indecşii celulelor goale (pe grila iniţială chiar sunt „goale”, dar în Z ele conţin ICP-urile candidaţilor posibili) şi avem două variante (după cum comentăm şi decomentăm cele două linii de program pentru Rest): fie păstrăm ordinea din grila iniţială a celulelor goale, fie ordonăm celulele goale după numărul de candidaţi (folosind restKand()); dar să observăm că în cazul de faţă este vorba de numărul de candidaţi existent în tabelul de bază al candidaţilor (păstrat intact în reshat()).
> source("solve1.R") # pentru "grid3.txt" Tabelul de bază al candidaţilor: # cele 25 de valori fixate iniţial sunt boldate [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 9 367 367 8 15 15 4 2 67 [2,] 5 1238 12348 6 7 24 1389 1389 19 [3,] 1246 12678 124678 3 24 9 168 1678 5 [4,] 7 4 268 1 2568 256 23569 3569 269 [5,] 126 12568 9 25 3 2456 7 156 126 [6,] 3 1256 126 9 256 7 1256 4 8 [7,] 8 12367 12367 4 1256 1256 12569 15679 12679 [8,] 1246 1267 12467 257 9 8 1256 1567 3 [9,] 126 9 5 27 126 3 1268 1678 4 Soluţia finală (prin backtracking pe secvenţa celulelor cu candidaţi): [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 9 6 3 8 5 1 4 2 7 [2,] 5 1 4 6 7 2 3 8 9 [3,] 2 7 8 3 4 9 6 1 5 [4,] 7 4 2 1 8 5 9 3 6 [5,] 6 8 9 2 3 4 7 5 1 [6,] 3 5 1 9 6 7 2 4 8 [7,] 8 3 7 4 1 6 5 9 2 [8,] 4 2 6 5 9 8 1 7 3 [9,] 1 9 5 7 2 3 8 6 4 clues: 25; fixed before 'backtracking': 30 timp (backtracking): 0.259 sec. ## cu 'Rest' neordonat total reveniri în secvenţa celulelor: 28296 ## cu 'Rest' neordonat ## respectiv, în varianta Rest <- restKand(Z): # timp (backtracking): 0.179 sec. ## cu 'Rest' ordonat # total reveniri în secvenţa celulelor: 17528 ## cu 'Rest' ordonat
Dar între cele două variante de parcurgere a celulelor „goale” (păstrând ordinea lor iniţială şi respectiv, ordonând după numărul de candidaţi), diferenţa de timp şi „număr de reveniri” poate să fie extrem de mare şi nu neapărat, în favoarea ordonării prealabile – cum demonstrează acest exemplu:
> source("solve1.R") # pentru "grid4.txt" Tabelul de bază al candidaţilor: # cele 21 de valori fixate iniţial sunt boldate [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 8 1246 24569 2347 12357 1234 13569 4579 1345679 [2,] 12459 124 3 6 12578 1248 1589 45789 14579 [3,] 1456 7 456 348 9 1348 2 458 13456 [4,] 123469 5 2469 2389 2368 7 1689 2489 12469 [5,] 12369 12368 269 2389 4 5 7 289 1269 [6,] 24679 2468 24679 1 268 2689 5689 3 24569 [7,] 23457 234 1 23479 237 2349 359 6 8 [8,] 23467 2346 8 5 2367 23469 39 1 2379 [9,] 23567 9 2567 2378 123678 12368 4 257 2357 Soluţia finală (prin backtracking pe secvenţa celulelor cu candidaţi): [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 8 1 2 7 5 3 6 4 9 [2,] 9 4 3 6 8 2 1 7 5 [3,] 6 7 5 4 9 1 2 8 3 [4,] 1 5 4 2 3 7 8 9 6 [5,] 3 6 9 8 4 5 7 2 1 [6,] 2 8 7 1 6 9 5 3 4 [7,] 5 2 1 9 7 4 3 6 8 [8,] 4 3 8 5 2 6 9 1 7 [9,] 7 9 6 3 1 8 4 5 2 clues: 21; fixed before 'backtracking': 21 timp (backtracking): 0.503 sec. ## cu 'Rest' neordonat total reveniri în secvenţa celulelor: 49498 ## cu 'Rest' neordonat ## respectiv, în varianta Rest <- restKand(Z): # timp (backtracking): 320.247 sec. ## cu 'Rest' ordonat # total reveniri în secvenţa celulelor: 31055126 ## cu 'Rest' ordonat
În acest caz şi timpul de execuţie şi numărul de reveniri sunt de peste 600 de ori mai mari, dacă celulele sunt analizate în ordinea numărului de candidaţi şi nu în ordinea iniţială a lor.
Evidenţierea revenirilor
Prin reshat() din programul precedent se fac aşa de multe reveniri, fiindcă eventuala invalidare a unui candidat „temporar bun” se constată abia după ce se „analizează” candidaţii (deasemenea, temporar buni) de pe o serie (care poate fi şi foarte lungă) de celule următoare celei curente.
Pentru a evidenţia cum se petrec lucrurile, copiem "solve1.R" în solve11.R şi în acest „nou” program, completăm funcţia reshat() (cu liniile marcate cu #1#, #2# şi #3#) şi excludem unele afişări (timp, număr de reveniri, etc.):
# solve11.R (evidenţiază traseele de căutare a candidaţilor buni) source("mysu.R") grd <- scan('grid3.txt', what = integer(), quiet=TRUE) Z <- fixgrid(aspire(grd)) # tabelul de bază al candidaţilor Rest <- which(!Z %in% FIX) # păstrează ordinea iniţială a celulelor lKan <- lapply(Rest, function(v) splitICP(Z[v])) Result <- NULL reshat <- function(Z, ref = 1) { if(ref > length(Rest)) { Result <<- Z return(TRUE) } cat(ref, ": ", which(FIX %in% lKan[[ref]]), " ", sep="") #1# idx <- Rest[ref] for(knd in lKan[[ref]]) { if(knd %in% Z[twe[[idx]]]) next cat(which(FIX == knd), "from", idx, "\n") #2# Z[idx] <- knd if(reshat(Z, ref + 1)) return(TRUE) } return(FALSE) } sink("trace1.txt") #3# reshat(Z) sink() cat("Tabelul de bază al candidaţilor:\n") printKand(Z) cat("\nSoluţia finală:\n") printKand(Result)
Am considerat iarăşi "grid3.txt", pentru care tabelul candidaţilor şi soluţia finală au fost deja redate mai sus. Prin sink(), din linia marcată cu #3#, am redirecţionat pe fişierul "trace1.txt" output-ul produs prin cat() din liniile #1# şi #2#; prin comenzile cat() respective, în "trace1.txt" se înscriu linii de forma:
ref: knds knd from idx_Z
unde ref reperează elementul curent din vectorul Rest, knds reprezintă candidaţii de pe celula lui Z cu indexul Rest[ref], iar knd este candidatul fixat temporar, dintre cei existenţi pe celula lui Z cu indexul idx_Z; subliniem că vor apărea situaţii în care celula de index Rest[ref] diferă de aceea vizată de idx_Z.
Prima linie din tabelul candidaţilor (cu elementele de indecşi 1:9 din Z) este: <1>
9 367 367 8 15 15 4 2 67
iar primele câteva linii din "trace1.txt" sunt acestea: <2>
1: 367 3 from 2
2: 367 6 from 3
3: 15 1 from 5
4: 15 5 from 6
5: 67 7 from 9
6: 1238 1 from 11
Să mai amintim şi prima linie din soluţia finală: <3>
9 6 3 8 5 1 4 2 7
Este uşor de interpretat împreună, <1>, <2> şi <3>.
Amintim că Rest conţine indecşii celulelor „goale”, 2, 3, 5, 6, 9, etc. (şi aici, am ales să păstrăm ordinea iniţială, în loc de a ordona după numărul de candidaţi).
Mai întâi, reshat() accesează celula indicată de Rest[1], deci Z[2], care conţine candidaţii "367"; dintre aceştia, chiar primul este „convenabil”, fiindcă nu se află în Z[twe[[2]]] (nici pe linia 1, nici pe coloana 2, nici în blocul B1) – astfel că "3" este fixat în celula Z[2].
Dar să observăm deja că nu poate fi vorba decât de o fixare temporară, fiindcă din <3> vedem că "6" este valoarea corectă pentru Z[2] şi nu "3".
După fixarea lui "3" pe Z[2], reshat() se autoapelează pentru următoarea celulă indicată în Rest, deci pentru Z[3], cu "367"; acum "3" este sărit (constatând că "3" există deja pe linia 1) şi este fixat "6" (temporar, cum vedem în <3>).
Mai departe, lucrurile decurg tot aşa, din aproape în aproape…
Dar curând, apare şi o situaţie mai interesantă – după ce se ajunge să se fixeze temporar celulele (boldate) corespunzătoare primilor 12 indecşi din Rest:
# după rezolvarea temporară a celulelor "goale" (cele boldate) din Z[1:19]
9 3 6 8 1 5 4 2 7
5 1 2 6 7 4 3 8 9
4 12678 124678 3 24 9 168 1678 5
7 4 268 1 2568 256 23569 3569 269
# liniile asociate în "trace1.txt", stadiului curent din reshat()
13: 12678 7 from 20
14: 124678 8 from 21
15: 24 2 from 23
16: 168 1 from 25
17: 1678 6 from 26
18: 268 6 from 25
17: 1678 1 from 26
18: 268 8 from 20
14: 124678 7 from 21
15: 24 2 from 23
Rest[13] referă celula Z[20]; primii trei candidaţi sunt respinşi (fiind deja în blocul B1) şi se fixează "7" (rămânând ca rezervă, "8"). Apoi, prin reapelare: se fixează "8" în celula lui Z de index 21 (pe care ceilalţi candidaţi nu mai sunt posibili, regăsindu-se deja în blocul B1), se fixează "2" la indexul 23, "1" la indexul 25 şi "6" la indexul 26.
Ajungând acum la celula referită de Rest[18], se constată că niciunul dintre candidaţii "268" nu este convenabil (fiindcă îi avem deja, pe aceeaşi coloană cu celula curentă, în urma fixărilor temporare precedente – menţionate mai sus); ca urmare, apelul curent reshat() returnează FALSE – ceea ce provoacă reconstituirea stării din apelul precedent: cu alte cuvinte, "1" care în apelul precedent, fusese fixat temporar în Z[25] este recunoscut ca fiind invalid şi este înlocuit cu următorul din lista "168" a candidaţilor, deci cu "6" – ca şi cum s-ar „executa” din nou linia "16: 168 1 from 25" din "trace1.txt", dar acum cu "6" în loc de "1".
Apoi se avansează din nou, la celula referită de Rest[17]; dintre candidaţii "1678" ai celulei Z[26], "1" este primul dar şi singurul care nu apare încă pe linie sau bloc; deci se fixează "1" în Z[26] şi se ajunge iarăşi la celula referită de Rest[18] – dar aici nu este convenabil niciunul dintre "268", încât se reconstituie cadrele din apelurile anterioare, unul câte unul, până când se găseşte o celulă pe care se poate înlocui candidatul fixat anterior cu un altul dintre cei rămaşi pe acea celulă (în speţă, se coboară până la celula Z[20], „reexecutând” linia "13:" cu "8" în loc de "7" şi reluând avansarea de la celula referită de Rest[14]).
Am ilustrat mai sus o situaţie „digerabilă” (cu distanţă scurtă de revenire); dar pentru "3", care a fost fixat din start pe Z[2] (corect era "6", cum am remarcat chiar de la început), revenirea se face tocmai în linia 21758 din "trace1.txt": "26: 25 6 from 2"; cu alte cuvinte, pentru a renunţa la "3" şi a încerca următorul candidat de pe Z[20], au fost necesare 21758 de treceri înainte şi înapoi, în secvenţa celor 51 de celule rămase de fixat funcţiei reshat().
Cunoscând această situaţie, am putea interveni (interactiv) pentru a elimina cele 21758 de curse stabilite mai sus ca fiind inutile: înainte de a lansa reshap(), modificăm ordinea "368" a candidaţilor celulei referite de Rest[1]:
sink("trace1.txt") #3# lKan[[1]] <- FIX[c(6, 3, 8)] # schimbă ordinea candidaţilor pe celula Z[Rest[1]]≡Z[2] reshat(Z) sink()
Relansând solve11.R, acum fişierul de trasare a execuţiei începe cu linia 1: 368 6 from 2, ceea ce înseamnă că în Z[2] se fixează valoarea care ştim că este cea corectă ("6", nu "3" ca în execuţia precedentă), iar "trace1.txt" are acum numai 6590 de linii (cu 21758 linii mai puţin decât în cazul execuţiei programului iniţial).
Obs. Programele cu "backtracking" sunt cotate de obicei prin „numărul de reveniri”; dar şi mai important(ă) ar fi calitatea acestor reveniri: pot să fie „lungi” (ca în cazul revenirii la "3", mai sus), sau pot să fie „scurte”. Chiar şi un singur caz de revenire „lungă”, va influenţa (foarte) negativ, execuţia programului.
Obs. Pentru o clasă întreagă de probleme rezolvate prin "backtracking", se poate proceda pentru evidenţierea traseului execuţiei, la fel cum am evidenţiat mai sus. Semnalăm deci o problemă interesantă: a produce din fişierul "trace1.txt" structura arborescentă a căutării efectuate în programul respectiv.
Un „program principal” în care filtrăm candidaţii
Dar putem filtra mai bine, candidaţii „temporar buni” – folosind fixgrid(cutKand()); salvăm "solve1.R" sub numele "solve2.R" şi modificăm apoi reshat() astfel:
# solve2.R (faţă de "solve1.R", se rescrie numai reshat()) reshat <- function(Z, ref = 1) { if(ref > length(Rest)) { Result <<- Z return(TRUE) } idx <- Rest[ref] for(knd in lKan[[ref]]) { if(knd %in% Z[twe[[idx]]]) next Z[idx] <- knd if(is.null(fixgrid(cutKand(Z)))) # filtru suplimentar de "temporar bun" next if(reshat(Z, ref + 1)) return(TRUE) } back <<- back + 1 return(FALSE) }
Se poate ca timpul de execuţie să crească faţă de primul program, dat fiind că acum implicăm (şi repetat) două noi apeluri de funcţii; timpul rămâne totuşi de ordinul a câtorva secunde – nici într-un caz, nu ajunge să fie de ordinul minutelor (mai înainte, "solve1.R" soluţionase "grid4.txt", cu ordonare prealabilă după candidaţi, în 5-6 minute). În schimb, numărul de reveniri ajunge să fie aproape nesemnificativ, faţă de cel rezultat în "solve1.R" (unde nu implicasem fixgrid(cutKand())):
grid3.txt
clues: 25; fixed before 'backtracking': 30
păstrând ordinea iniţială: ## prin "solve1.R":
timp (backtracking): 2.088 sec. # 0.259 sec.
total reveniri în secvenţa celulelor: 73 # 28296
ordonând în prealabil după numărul candidaţilor:
timp (backtracking): 0.684 sec. # 0.179 sec.
total reveniri în secvenţa celulelor: 6 # 17528
grid4.txt
clues: 21; fixed before 'backtracking': 21
păstrând ordinea iniţială: ## prin "solve1.R":
timp (backtracking): 1.496 sec. # 0.503 sec.
total reveniri în secvenţa celulelor: 30 # 49498
ordonând în prealabil după numărul candidaţilor:
timp (backtracking): 6.809 sec. # 320.247 sec.
total reveniri în secvenţa celulelor: 296 # 31055126
De remarcat că în cazul "grila3.txt" ordonarea prealabilă (după numărul de candidaţi) este preferabilă şi ca timp de soluţionare şi ca număr de reveniri; însă pentru "grila4.txt" este mai mult decât „preferabilă”, ordinea iniţială a celulelor.
Un „program principal” mai bun
În solve2.R am angajat fixgrid(cutKand()) în reshap(), numai pentru a vedea dacă rezultatul este NULL (ceea ce invalidează deja, candidatul curent – permiţând abandonarea acestuia şi angajarea imediată a celui următor). fixgrid(cutKand()) modifică tabelul candidaţilor (reducând prin simplify(), anumiţi candidaţi dintre cei postaţi iniţial pe divese celule) şi n-am putut folosi efectiv rezultatul (decât dacă este NULL), câtă vreme am formulat reshap() ca parcurgere a secvenţei de celule „goale” – fixate iniţial prin Rest – din tabelul de bază (iniţial) al candidaţilor.
Ideea unui program „mai bun” este simplă: angajăm fixgrid(cutKand()) pe o copie W a lui Z, pentru care determinăm Rest-ul corespunzător după reducerea de candidaţi rezultată şi reapelăm reshat() pentru W şi noul Rest (în caz că reshat() va returna FALSE, se va recupera eventual, vectorul Z iniţial).
Salvăm "solve2.R" ca "solve3.R" şi rescriem funcţia reshat(), renunţând să mai vizăm consecutiv celulele indicate de vectorul Rest iniţial (şi putem elimina lista lKan):
# solve3.R (modifică reshat() faţă de 'solve2.R') source("mysu.R") grd <- scan('grid3.txt', what = integer(), quiet=TRUE) Z <- fixgrid(aspire(grd)) Rest <- restKand(Z) function(v) splitICP(Z[v])) Result <- NULL back <- 0 reshat <- function(Z, idx = Rest[1]) { if(is.na(idx)) { Result <<- Z return(TRUE) } knds <- splitICP(Z[idx]) for(knd in knds) { if(knd %in% Z[twe[[idx]]]) next Z[idx] <- knd W <- fixgrid(cutKand(Z)) # introduce o copie a lui Z (protejând Z_curent) if(is.null(W)) next if(reshat(W, restKand(W)[1])) # continuă pe W şi "Rest"-ul corespunzător return(TRUE) } back <<- back + 1 return(FALSE) } u <- system.time(reshat(Z)) ## secvenţa de afişare a unor informţii (v. "solve1.R")
Redăm informaţiile de execuţie, pentru cele două grile vizate şi în "solve2.R":
grid3.txt clues: 25 ; fixed before 'backtracking': 30 timp (backtracking): 0.365 sec. ## 0.684 sec., prin "solve2.R" total reveniri în secvenţa celulelor: 15 ## numai 6, prin "solve2.R" grid4.txt clues: 21 ; fixed before 'backtracking': 21 timp (backtracking): 1 sec. ## 6.809 sec., prin "solve2.R" total reveniri în secvenţa celulelor: 41 ## 296, prin "solve2.R"
Timpul de execuţie este mai bun decât în cazul lui "solve2.R"; probabil că „numărul de reveniri” este totdeauna mai bun, dacă ne gândim nu numai la „număr”, dar şi la calitatea revenirilor (pare clar că nu vor exista reveniri „lungi”, având în vedere că acum reapelările reshat() lucrează pe tabele reduse, în urma implicării funcţiilor fixgrid() şi cutKand()).
Putem îmbunătăţi cumva timpul?
Folosind programul utilitar Rprof, putem constata cam cum este repartizat timpul de execuţie între funcţiile apelate din reshat(); de fapt, obţinem o confirmare a bănuielii evidente, că fixgrid() şi cutKand() (cu funcţia apelată de acestea, simplify()) consumă cel mai mult din acest timp. Nu prea credem că am putea îmbunătăţi (în mod semnificativ) aceste funcţii, dar o mică încercare este totuşi instructivă.
Şi în fixgrid() şi în cutKand() se calculează de câte două ori (la fiecare apelare) numărul curent de valori fixate, folosind operatorul '%in%'; dar valorile din FIX sunt de forma 2k, iar condiţia ca v să fie putere a lui 2 este bitwAnd(v, v-1) == 0. Deci am avea două variante de calcul şi ar fi de văzut care este „mai bună”:
source("mysu.R") grd <- scan('grid9.txt', what = integer(), quiet=TRUE) Z <- fixgrid(aspire(grd)) # Z <- rep(Z, 100) ## pentru un vector mai lung nfix <- function(Z) length(Z[Z %in% FIX]) nfix1 <- function(Z) length(Z[bitwAnd(Z, Z - 1L) == 0]) u <- system.time(for(i in 1:10000) n <- nfix(Z)) print(u) u <- system.time(for(i in 1:10000) n <- nfix1(Z)) print(u) # user system elapsed # 0.044 0.005 0.049 ## cu '%in%' # user system elapsed # 0.037 0.000 0.038 ## cu testul pentru 2k
Există o diferenţă de timp între cele două variante, vizibilă dacă le repetăm de suficient de multe ori; pentru cele 10000 de repetări din programul redat mai sus, diferenţa a ajuns pe la 10 milisecunde, în favoarea testului de putere a lui 2.
Putem constata că de exemplu pentru "grid9.txt", numărul de apeluri ale funcţiei fixgrid() (prin execuţia programului "solve3.R") este 2073; deci fixgrid(cutKand()) se apelează cam de 4000 de ori (iar cutKand() se mai apelează repetat şi din simplify()), deci numărul de valori fixe din Z se calculează de peste 16000 de ori – încât ar rezulta într-adevăr, o anumită îmbunătăţire a timpului (dar numai cu vreo 10-15 milisecunde), dacă vom adopta a doua variantă. Vom prefera totuşi prima variantă, fiind parcă mai sigură („ţine” şi în cazul în care bitwAnd() ar da eroarea parcă mai greu digerabilă, "'a' and 'b' must have the same type").
Adevărata îmbunătăţire, a timpului…
Posibila îmbunătăţire (în mod semnificativ) a timpului de execuţie este ascunsă cel mai degrabă, în însăşi formularea existentă pentru funcţiile respective.
Să observăm această secvenţă preluată direct din cutKand():
for(i in which(Z %in% FIX)) { # pentru valorile curent fixate v <- Z[i] tw <- twe[[i]] # indecşii colegilor celulei curente for(j in tw) # anulează candidatura lui v pe câmpurile colegilor if(bitwAnd(Z[j], v) > 0) Z[j] <- bitwAnd(Z[j], bitwNot(v)) if(0 %in% Z) # sistează, dacă rezultă colegi identici! return(NULL) }
Pe Z[i] s-a fixat deja o valoare din FIX, iar acum, pentru fiecare dintre celulele „colege” – adică pentru fiecare celulă Z[j] indicată în lista twe[[i]] – se testează dacă printre candidaţii acesteia figurează şi Z[i] şi în caz afirmativ, se exclude Z[i] dintre candidaţii existenţi pe celula Z[j] (folosind bitwAnd() şi bitwNot()); dacă în final, în Z[j] rămâne cumva 0, atunci cutKand() returnează imediat NULL.
Avem aici un foarte bun exemplu de „rele practici” de folosire a limbajului R!
Mai întâi, testul prealabil if(bitwAnd(Z[j], v) > 0) nu este neapărat necesar, fiindcă dacă v nu face parte dintre candidaţii de pe Z[j] atunci atribuirea cu bitwAnd(Z[j], bitwNot(v)) care urmează acestui test nu modifică de fapt, Z[j].
Prin urmare, putem considera (îndepărtând "if()"-ul menţionat) că pe toate celulele indicate în twe[[i]] se face o aceeaşi operaţie (de atribuire). Atunci, lucrurile pot fi instrumentate în maniera vectorială specifică pentru R – deodată pentru toţi colegii, în loc de individual, pentru fiecare în parte:
for(i in which(Z %in% FIX)) { # pentru valorile curent fixate v <- Z[i] tw <- twe[[i]] # indecşii colegilor celulei curente Z[tw] <- bitwAnd(Z[tw], bitwNot(v)) # elimină v la colegii lui Z[i] if(any(Z[tw] == 0)) # ceva mai avantajos ca if(0 %in% Z) return(NULL) }
Cu această modificare în cutKand(), obţinem acum un timp sensibil mai bun; de exemplu, relansând solve3.R pentru "grila4.txt" avem soluţia în 0.4 secunde, în timp ce anterior (v. mai sus) o obţinusem în 1 secunde.
În final, un program cu tentă nedeterministă
În solve3.R am procedat chiar nostim: am ordonat celulele rămase de fixat, după numărul de candidaţi pe câmp (folosind restKand()), dar din vectorul ordonat obţinut am folosit (în reshat()) numai primul index (scuza ar fi că faţă de "solve2.R" în care foloseam întregul vector, am rescris doar reshat()).
În loc de restKand(), introducem în mysu.R o funcţie care (folosind which.min()) furnizează indexul unui câmp pe care avem numărul minim de candidaţi:
nKand <- function(icp) { # numărul de candidaţi (biţi 1) g2 <- bitwAnd(icp, FIX) length(g2[g2 > 0]) } firstSqr <- function(Z) { Rest <- which(!Z %in% FIX) sq <- which.min(lapply(Z[Rest], nKand)) Rest[sq] # indexul unui câmp cu numărul minim de candidaţi (cel puţin doi) }
Salvăm "solve3.R" în "solve4.R"; este uşor de rescris funcţia reshat(), înlocuind restKand() – şi restKand()[1] – cu firstSqr():
# solve4.R source("mysu.R") grd <- scan('grid4.txt', what = integer(), quiet=TRUE) Z <- fixgrid(aspire(grd)) # tabelul de bază al candidaţilor Rest <- firstSqr(Z) # indexul primei celule cu numărul minim de candidaţi Result <- NULL # back <- 0 # numărul de reveniri reshat <- function(Z, idx = Rest) { if(length(idx) == 0) { Result <<- Z return(TRUE) # se presupune că soluţia este unică } knds <- sample(splitICP(Z[idx])) # ordinea abordării este foarte importantă! for(knd in knds) { if(knd %in% Z[twe[[idx]]]) next Z[idx] <- knd W <- fixgrid(cutKand(Z)) if(is.null(W)) next if(reshat(W, firstSqr(W))) # încearcă următorul candidat return(TRUE) } return(FALSE) }
În programele anterioare foloseam "back", pentru a contoriza revenirile din reshat() şi ne-am convins că, implicând la fiecare pas fixgrid(cutKand()), asigurăm un număr relativ mic de reveniri – încât acum, am renunţat la contorul respectiv (care nici nu reflectă, cum ar fi de dorit, calitatea revenirilor respective).
Noutatea importantă este aceea că acum, candidaţii de pe celula curentă sunt investigaţi nu în ordinea în care apar în ICP-ul respectiv, ci într-o ordine aleatorie (folosind sample()). Bineînţeles că până a decide astfel, am experimentat cu un criteriu de alegere „determinist” – angajând candidaţii celulei curente în ordinea inversă a numărului de fixări (temporare sau definitive); dar instrumentarea unor asemenea criterii de alegere este anevoioasă iar efectele pozitive sunt incerte.
Abordând candidaţii celulei în ordine aleatorie, realizăm că măcar una dintre două-trei-patru execuţii ale programului, va produce soluţia şi într-un timp mult mai scurt decât în cazul ordonării obişnuite.
Să facem o statistică a timpului de execuţie, pentru 100 de rulări consecutive ale funcţiei reshat() – completând "solve4.R" cu secvenţa următoare:
stat <- vector("numeric", 100) printKand(Z) for(i in 1:100) { u <- system.time(reshat(Z)) stat[i] <- u["elapsed"] } printKand(Result) print(summary(stat)) ## lansăm "solve4.R" (pentru grila din "grid4.txt"): > source("solve4.R") [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 8 1246 24569 2347 12357 1234 13569 4579 1345679 [2,] 12459 124 3 6 12578 1248 1589 45789 14579 [3,] 1456 7 456 348 9 1348 2 458 13456 [4,] 123469 5 2469 2389 2368 7 1689 2489 12469 [5,] 12369 12368 269 2389 4 5 7 289 1269 [6,] 24679 2468 24679 1 268 2689 5689 3 24569 [7,] 23457 234 1 23479 237 2349 359 6 8 [8,] 23467 2346 8 5 2367 23469 39 1 2379 [9,] 23567 9 2567 2378 123678 12368 4 257 2357 [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] 8 1 2 7 5 3 6 4 9 [2,] 9 4 3 6 8 2 1 7 5 [3,] 6 7 5 4 9 1 2 8 3 [4,] 1 5 4 2 3 7 8 9 6 [5,] 3 6 9 8 4 5 7 2 1 [6,] 2 8 7 1 6 9 5 3 4 [7,] 5 2 1 9 7 4 3 6 8 [8,] 4 3 8 5 2 6 9 1 7 [9,] 7 9 6 3 1 8 4 5 2 Min. 1st Qu. Median Mean 3rd Qu. Max. 0.0360 0.2382 0.3075 0.3052 0.4080 0.5600
Pentru "grid4.txt", cu "solve3.R" obţinusem soluţia în 0.4 sec.; acum am obţinut-o, repetând execuţia programului "solve4.R", în cel mai puţin 0.036 sec. şi cel mai mult 0.56 sec., iar timpul mediu este cam cu 100 de milisecunde mai scurt.
Putem încheia de-acum, cu „programele principale”: decupăm funcţia reshat() din "solve4.R" şi o adăugăm într-o copie su_doku.R a lui mysu.R (păstrând mysu.R, pentru eventualitatea unor noi experimente cu „programe principale” solve*.R).
Un experiment irelevant (pe un set prost de grile)
Pasionaţii de "rezolvare logică" pot găsi pe Internet milioane de grile Sudoku (în forma adecvată – ca fişier PDF, sau ca fişier-imagine, sau bineînţeles drept tipărituri de cumpărat). De la sudoku-download.net am descărcat un fişier PDF conţinând (citez) "30 very difficult Sudoku puzzles"; prin iLovePDF.com l-am redus la un fişier ".xlsx", pe care apoi l-am transformat prin Gnumeric în 5 fişiere CSV (câte unul pentru fiecare dintre foile Excel conţinute); am concatenat fişierele CSV respective (după ce am eliminat rândurile cu numărul de diagramă şi numărul paginii PDF) – rezultând în sfârşit, acel fişier-text foarte simplu care ar fi fost de oferit de la bun început:
1,2,3,4,5,6,7,8,9 # antetul CSV (numele câmpurilor) 4,5,,,,,,, # prima diagramă (grilă) ,,2,,7,,6,3, ,,,,,,,2,8 ,,,9,5,,,, ,8,6,,,,2,, ,2,,6,,,7,5, ,,,,,,4,7,6 ,7,,,4,5,,, # a doua diagramă ,,8,,,9,,, ## etc. (225 de linii - deci 25 de grile)
Cu siguranţă că mi-a scăpat o foaie, pe parcursul operaţiilor stupide pe care le-am evocat mai sus, fiindcă în "30svd.csv" mi-au rezultat nu 30, ci numai 25 de grile…
În programul următor transformăm fişierul CSV respectiv într-o listă de vectori (folosind „dialectul” tidyverse):
library(tidyverse) svd <- read_csv("30svd.csv", col_types="iiiiiiiii") svd[is.na(svd)] <- 0 # A tibble: 225 x 9 # `1` `2` `3` `4` `5` `6` `7` `8` `9` # <int> <int> <int> <int> <int> <int> <int> <int> <int> # 1 4 5 0 0 0 0 0 0 0 # 2 0 0 2 0 7 0 6 3 0 svd$grd <- factor(rep(1:25, each=9)) # etichetează liniile după rangul diagramei grids <- svd %>% split(.$grd) %>% # câte un 'tibble' de fiecare diagramă map(., function(G) { G$grd <- NULL # elimină etichetele de pe linii as.vector(t(data.matrix(G))) }) saveRDS(grids, "25grids.RDS") # listă cu 25 de vectori a câte 81 întregi (25 grile)
Cu următorul program aplicăm reshat() fiecăreia dintre grilele din lista obţinută mai sus şi înscriem rezultatele execuţiei în fişierul "30svd.rst":
source("su_doku.R") svd <- readRDS("25grids.RDS") sink("30svd.rst") for(i in 1:25) { back <- 0 grd <- svd[[i]] Z <- fixgrid(aspire(grd)) printKand(Z) # tabloul de bază al candidaţilor u <- system.time(reshat(Z)) printKand(Result) # soluţia grilei cat(i, ": back=", back, "; timp=", u["elapsed"], sep="", "\n\n") } sink()
Am reînfiinţat contorul "back", pentru a vedea şi numărul de reveniri… Dar – surpriză: programul redat a durat doar o mică fracţiune de secundă (mă aşteptam să fie vreo câteva minute, dată fiind atenţionarea de "very difficult puzzle"), iar toate rezultatele obţinute în "30svd.rst" sunt de forma:
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 4 5 3 8 2 6 1 9 7
[2,] 8 9 2 5 7 1 6 3 4
[3,] 1 6 7 4 9 3 5 2 8
[4,] 7 1 4 9 5 2 8 6 3
[5,] 5 8 6 1 3 7 2 4 9
[6,] 3 2 9 6 8 4 7 5 1
[7,] 9 3 5 2 1 8 4 7 6
[8,] 6 7 1 3 4 5 9 8 2
[9,] 2 4 8 7 6 9 3 1 5
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 4 5 3 8 2 6 1 9 7
[2,] 8 9 2 5 7 1 6 3 4
[3,] 1 6 7 4 9 3 5 2 8
[4,] 7 1 4 9 5 2 8 6 3
[5,] 5 8 6 1 3 7 2 4 9
[6,] 3 2 9 6 8 4 7 5 1
[7,] 9 3 5 2 1 8 4 7 6
[8,] 6 7 1 3 4 5 9 8 2
[9,] 2 4 8 7 6 9 3 1 5
1: back=0; timp=0.012
Adică, la toate cele 25 de grile, în loc de tabloul de bază al candidaţilor (rezultat din grila iniţială, înainte de a angaja reshat()) avem chiar soluţia problemei; la toate, back este în final 0, iar timpul de execuţie pentru reshat este numai în trei cazuri, diferit de 0 (şi nu mai mare ca 12 milisecunde).
Prin urmare, toate cele 25 de grile, clamate la sursa lor ca "very difficult", se rezolvă direct, aplicând cele două reguli simple pe care le-am modelat în simplify() – ceea ce este prea puţin relevant (nu are sens nicio statistică) pentru programul nostru.
Un experiment pe un set consistent de grile
Vrem totuşi să investigăm comportarea programului nostru pe un set mai larg de grile (care să fie şi adecvate). În postări mai vechi, în diverse locuri, am găsit şi fişiere "text" conţinând grile Sudoku (chipurile, de clasă "Hardest"). Concatenăm trei astfel de fişiere (în care grilele au un acelaşi format textual; la ultimul însă, a trebuit să eliminăm în prealabil, câmpurile anexate grilelor, precum ",HardestSudokusThread-00001;..."):
vb@Home:~/21iun/mySuDoku$ \
> cat hardest.txt top95.txt HardestDb110626.txt > HgridSet.csv
HgridSet.csv conţine o singură coloană de date (pe care am denumit-o "grid"), cu 481 de valori (şiruri de caractere, reprezentând câte o grilă Sudoku):
grid # antetul fişierului CSV 85...24..72......9..4.........1.7..23.5...9...4...........8..7..17..........36.4. ..53.....8......2..7..1.5..4....53...1..7...6..32...8..6.5....9..4....3......97.. ### ş.a.m.d.
Prin programul utilitar (în Linux) uniq, constatăm că grilele respective sunt distincte între ele (provenind din fişiere diferite, erau posibile duplicate şi atunci, le-am fi eliminat).
În programul următor, constituim din "HgridSet.csv" un obiect "tibble", căruia îi prevedem încă trei coloane – pentru a înregistra pentru fiecare grilă, soluţia, numărul de reveniri şi timpul de execuţie – şi apoi, lansăm reshat() pe fiecare grilă:
library(tidyverse) hgs <- read_csv("HgridSet.csv", col_types="c") %>% mutate(sol = "", back = 0L, mls = 0L) source("su_doku.R") printSol <- function(Z) { mat <- sapply(Z, convICP); gsub(", ", "", toString(mat)) } for(i in 1:nrow(hgs)) { H <- gsub("\\.", "0", hgs[i, 1], perl=TRUE) grd <- as.integer(unlist(strsplit(H, split=NULL, perl=TRUE))) back <- 0 u <- system.time({ Z <- fixgrid(aspire(grd)) reshat(Z) }) hgs[i, 2] <- printSol(Result) hgs[i, 3] <- back hgs[i, 4] <- round(1000*u["elapsed"]) # milisecunde } saveRDS(hgs, file="hgs.RDS") # "hgs1.RDS" etc., dacă repetăm execuţia programului
Desigur, grila citită din fişierul CSV în prima coloană a „tabelului” hgs a trebuit să fie transformată, mai întâi înlocuind '.' cu '0' (prin gsub()) şi apoi convertind (prin strsplit(), etc.) în vectorul de întregi cerut de aspire(). Subliniem că am măsurat timpul de execuţie a lui reshat() împreună cu fixgrid(aspire()).
Programul redat s-a executat cam în 7 minute, ceea ce înseamnă că prelucrarea unei grile dintre cele 481 a luat în medie, aproape o secundă. Pe seama datelor obţinute în hgs.RDS, putem face acum unele statistici (şi eventual, grafice statistice) relevante pentru comportarea programului su_doku.R:
> summary(hgs$back) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.0 22.0 82.0 135.2 194.0 1013.0 > summary(hgs$mls) Min. 1st Qu. Median Mean 3rd Qu. Max. 8.0 160.0 533.0 804.2 1119.0 6052.0 > ggplot(data=hgs, aes(x=back, y=mls)) + + geom_point() + geom_smooth(method="lm") + geom_rug()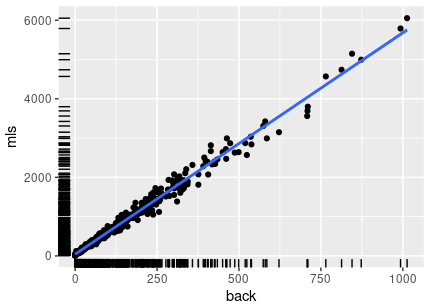
Deci 25% dintre grile au fost soluţionate într-un timp cuprins între 8 şi 160 milisecunde, revenind în reshat() de cel mult 22 de ori; pentru 50% dintre grile, mls este în intervalul (160, 1119) milisecunde, iar back în intervalul (22, 194); pentru restul de 25%, mls este cel mult 6.052 sec., iar back este cel mult 1013.
Grafic, grilele sunt reprezentate ca puncte raportate la back şi mls; observăm că avem foarte puţine puncte (grile) care depăşesc limita (500, 2500) – am numărat 17 puncte, dar putem constata direct:
> hgs %>% filter(back > 500) %>% nrow(.) [1] 17 # 17 grile cu 'back' > 500
Tot aşa, putem constata că pentru 20 de grile avem back == 0 (adică fixgrid(aspire(grd)) a completat deja toate valorile necesare soluţiei); iar pentru 444 de grile dintre cele 481 (corespunzătoare aproximativ punctelor masate în jurul primei treimi a dreptei „de regresie”, trasate cu albastru), avem back < 375.
Se confirmă şi bănuiala evidentă că mls creşte proporţional cu back; considerând numai primele 3 quartile şi raportând creşterea lui mls la cea a lui back (1111/194) deducem (cam empiric, desigur) că o revenire în reshat() (reluând pe o altă ramură, de pe un nivel anterior) a costat în medie cam 5.7 milisecunde.
Desigur, dacă reluăm într-un alt moment execuţia programului, vom obţine alte valori pentru statisticile redate mai sus (fiindcă în reshat() am implicat şi un aspect aleatoriu, folosind sample()) – dar este de aşteptat ca în medie (presupunând un număr rezonabil de reexecutări) limitele şi proporţiile să nu diferă sensibil, faţă de acestea.
vezi Cărţile mele (de programare)