[1] manual Algebră, cl. a XII-a, capitolul "Polinoame" (autor: prof. Mircea Ganga)

[2] Polynomial_greatest_common_divisor

Pentru expresiile matematice folosim aici biblioteca MathJax. Eventual: click-dreapta pe una dintre formulele respective, Math Settings -> Math Renderer -> MathML (Firefox, Chrome, Opera).

Cum şade bine unei probleme, enunţul nu spune totul (dar nici nu ascunde ceva) - lăsând "utilizatorului" şansa de a-şi lămuri lucrurile; putem confunda "relaţie liniară" cu obişnuita "combinaţie liniară" (când - cel mai frecvent - parametrii sunt nişte constante numerice).

De fapt, putem exclude din start cazul când `alpha` şi `beta` ar fi coeficienţi reali, fiindcă atunci `alpha f + beta g` ar fi (în general) un polinom de grad 4 (ori `d` are cel mult gradul 3). Parametrii respectivi sunt polinoame (şi mai bine se notau de exemplu 'u' şi 'v', ca în [2] şi nu prin litere greceşti cum se obişnuieşte pentru parametri numerici), iar "relaţie liniară" se referă la `f` şi `g` (nu la nedeterminata `X`).

Se vede uşor (folosind schema lui Horner) că avem:

Rezultă imediat că:

Cel mai uşor de constatat (prin "metoda coeficienţilor nedeterminaţi") este faptul că nu putem avea `alpha` de grad zero şi `beta` de grad 1, satisfăcând `alpha f + beta g` = 1. Ar trebui încercat cu polinoame de grad 1 şi 2, etc.; dar binevenitul "răspuns" indicat în manual ne salvează de la continuare: ni se spune întâi că `d` este `(X-1)(X+2)` şi nu 1, cum am găsit noi…

Să nu facem caz că "enunţul este greşit": în fond, problema se poate pune pentru oricare polinoame `f` şi `g` - vom şi reveni mai la sfârşit, asupra celor din enunţul "greşit". Putem încerca să ghicim acea corectură minimală a expresiei lui `g` încât şi acesta să aibă rădăcinile 1 şi -2:

Înlocuind termenul liber '-2' din polinomul iniţial `g` cu '-4', dăm peste rezultatul furnizat în manual. Să vedem acum dacă putem determina `alpha` = constant şi `beta` = `uX + v`; simplificând prin `d`, relaţia care trebuie satisfăcută devine:

şi identificând coeficienţii din cei doi membri găsim `alpha = -1 / 3` şi `u = v = 1 / 3` - adică

Răspunsul se putea da şi prin `d = -f + (X+1)g` fiindcă în cazul polinoamelor vorbim de un cel mai mare divizor comun: `3d` este deasemenea, un cel mai mare divizor comun.

Răspunsul se confirmă în [1] şi… putem trece la punctul următor - aceeaşi problemă, dar cu

Dintre rădăcinile lui `g` (rădăcinile de ordinul 5 ale unităţii) numai 1 este rădăcină şi pentru `f`, deci `d = X - 1`. Simplificând prin `d` relaţia de satisfăcut este:

Posibilitatea unor parametri de grad 1 sau 2 se exclude uşor (folosind metoda coeficienţilor nedeterminaţi); încercăm să satisfacem relaţia cu polinoame de gradul 3:

pentru care găsim următoarele relaţii (prin identificarea coeficienţilor):

Poate că acest sistem este uşor de rezolvat, dar putem avea cazuri (pentru alte polinoame iniţiale) când rezolvarea manuală ar fi greoaie; este de dorit deprinderea folosirii unui interpretor specializat pe calcul numeric - de exemplu, GNU Octave.

Constituim un fişier "solve.m" (".m" este extensia obişnuită pentru scripturi Octave - probabil de la "math"), în care definim matricea coeficienţilor A şi vectorul termenilor liberi B - soluţia fiind apoi obţinută prin operatorul Octave "\" între A şi B:

# "solve.m" (script Octave)
A = [ \ 
# a  b  c  d  u  v  w  t
  1  0  0  0  1  0  0  0;   # ';' separă liniile matricei
  0  1  0  0  1  1  0  0;
  1  0  1  0  1  1  1  0;
  0  1  0  1  1  1  1  1;
  2  0  1  0  1  1  1  1;
  0  2  0  1  0  1  1  1;
  0  0  2  0  0  0  1  1;
  0  0  0  2  0  0  0  1];  # ';' la sfârşit evită afişarea matricei constituite

B = [0; 0; 0; 0; 0; 0; 0; 1];

A \ B  # rezolvă AX = B (şi afişează răspunsul, neavând la sfârşit ';')

vb@vb:~$ octave solve.m
GNU Octave, version 3.2.4
Copyright (C) 2009 John W. Eaton and others.
# ... #
ans =     # answer
   0.090909 # a
  -0.090909 # b
   0.272727 # c
   0.545455 # d
  -0.090909 # u
   0.181818 # v
  -0.454545 # w
  -0.090909 # t

Fracţia 0.(09) care a apărut în răspuns reprezintă 1/11 şi toate valorile găsite sunt multipli de 1/11. Rezultă descompunerea "liniară":

şi elevii au acceptat că este rezultatul cerut (ar mai fost un hop de trecut: factorul 1/11 - prezent în mod implicit, mai sus - apare pe răspunsul din [1] numai la primul termen).

Soluţia prezentată mai sus foloseşte în principal "metoda coeficienţilor nedeterminaţi"; dar poate fi de bănuit că intenţia problemei (care apare ancorată în grupul problemelor cu tema "cel mai mare divizor comun") a fost aceea de a exersa algoritmul lui Euclid "extins". Amintim aici acest algoritm, dar vizăm explicit numai cazul numerelor întregi…

Pentru numere, problema formulată mai sus pentru cazul polinoamelor ar suna astfel:

În tabelul de calcule succesive următor, plecăm pentru exemplu cu A = 100 şi B = 64; determinăm restul R şi câtul Q al împărţirii lui A la B şi (dacă R încă nu a coborât la 0) mutăm valoarea curentă din coloana B în coloana A şi deasemenea, valoarea curentă din R în B - reluând împărţirea ultimei valori adăugate în coloana A prin aceea tocmai adăugată în coloana B:

    A    B    R    Q    # A = B*Q + R cu 0 ≤ R < B
    100  64   36   1
    64   36   28   1
    36   28   8    1
    28   8    4    3
    8    4    0    2

Exprimarea căutată (cel mai mare divizor comun în funcţie de A şi B) revine la a exprima ultima valoare nenulă din coloana R, în funcţie de valorile de pe prima linie din coloanele A şi B - deci avem de parcurs în ordine inversă liniile calculate mai sus, ţinând cont de două lucruri: pe fiecare linie avem `R = A - Q*B`, iar B este valoarea R de pe linia de deasupra celei curente.

De pe penultima linie avem exprimarea divizorului 4 în funcţie de A=28 şi B=8:

iar de pe linia de deasupra acesteia avem 8 = 36 - 1*28 şi obţinem descompunerea în funcţie de A=36 şi B=28:

Apoi, 28 = 64 - 1*36 şi obţinem descompunerea în funcţie de A=64 şi B=36:

Mai departe, 36 = 100 - 1*64 şi obţinem descompunerea finală, faţă de A=100 şi B=64:

Pentru cazul polinoamelor, gestionarea manuală a împărţirilor şi a calculelor "de jos în sus" este cel puţin incomodă, mai apărând şi dificultăţi artificiale (pentru a evita coeficienţi fracţionari - a vedea de exemplu [2], unde este redat şi un "Extended GCD algorithm", formulat iterativ).

Următoarea funcţie Python modelează cel mai simplu (recursiv) algoritmul descris mai sus:

def alg_euclid_ext(a, b):
    """ exprimă CMMDC ca o combinaţie liniară de a, b """
    if b == 0:
        return (a, 1, 0)
    q, r = divmod(a, b)
    #print (a, b, r, q)  # dacă vrem tabelul liniilor A,B,R,Q
    (d, x, y) = alg_euclid_ext(b, r) # d = x*A_curent + y*B_curent
    #print d, x, y  # exprimările d pe fiecare linie (A, B) a tabelului
    return (d, y, x - q*y)
    
print alg_euclid_ext(100, 64)  

Cu acest script, obţinem tabelul de calcule redat mai sus şi relaţiile "de jos în sus" aferente:

vb@vb:~/colanrug/DOC$ python exteuc.py 
(100, 64, 36, 1)
(64, 36, 28, 1)
(36, 28, 8, 1)
(28, 8, 4, 3)
(8, 4, 0, 2)   # 4 = cmmdc(100, 64)
4 1 0
4 0 1
4 1 -3       # 4 = 1*28 -3*8
4 -3 4       # 4 = -3*36 + 4*28
4 4 -7       # 4 = 4*64 - 7*36
(4, -7, 11)  # 4 = -7*100 + 11*64

Pentru polinoame, gestionarea manuală a calculelor cerute de algoritmul amintit mai sus este incomodă, până la greoaie; este mai uşor până la urmă, de scris un program care să furnizeze descompunerea cerută - şi încă, pentru oricare polinoame iniţiale.

De fapt, putem găsi funcţii gcdex(f, g) care rezolvă această problemă, în diverse limbaje. De exemplu SymPy este o bibliotecă Python care între altele implementează şi "gcdex()"; în plus, site-ul respectiv oferă şi o consolă SymPy interactivă, pe care oricine poate tasta direct comanda necesară pentru obţinerea rezultatului (fără să fie necesară instalarea bibliotecii şi altfel - cu o documentare prealabilă de 5 minute).

Astfel, introducând polinoamele din enunţul iniţial f = x**4 + 4*x**3 - 7*x + 2 şi g = x**3 + 3*x**2 -2 (nu -4, cum am corectat mai la început pentru a obţine rezultatul din manual), găsim rezultatele `alpha`, `beta` următoare:

Desigur, problema - nr. 54, pag.248 pe ediţia [1] din 2002 - prevede şi un al treilea punct, pentru care găsim acum imediat (fără să mai "rezolvăm"):

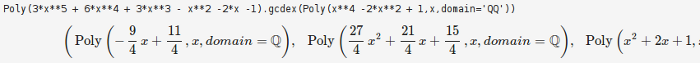
adică d = x² + 2x + 1, iar `alpha` şi `beta` sunt indicate în primele două "Poly" (şi într-adevăr, acesta este şi rezultatul dat în manual).

Am considerat numai `QQ[X]`, dar putem aborda şi cazul polinoamelor din `\ZZ_(bb p )[X]` cu `bb p` prim:

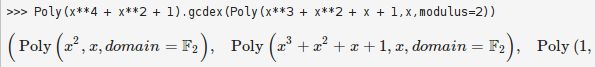
Am găsit astfel că pentru polinoamele din `\ZZ_(bb 2 )[X]`, `bb f = X^4 + X^2 + 1` şi `bb g = X^3 + X^2 + X + 1`, avem `bb d = 1` şi descompunerea liniară: `1 = X^2 bb f + (X^3 + X^2 + X + 1) bb g`; desigur, în acest caz - operând modulo 2 - nici operarea manuală a algoritmului n-ar fi dificilă:

Faţă de tabelul de calcul "A B R Q" prezentat mai sus pentru numere, acum nu am mai explicitat termenii "Q" şi am calculat exprimările "R" pe fiecare linie, "de sus în jos" (ceea ce este mai practic). Desigur, am ţinut cont de faptul că în `ZZ_bb 2` avem -1=1; astfel, `R = A - BQ = A + BQ`, `X + X = 0`, etc.