Producţii De Bruijn dintr-un model minimal de graf
Redăm aici un experiment rezultat din [1]; aveam nevoie de un model C++ pentru grafuri care să ofere un minimum de facilităţi, dar care să poată fi extins cu uşurinţă prin derivare.
Un model minimal de "graf", adecvat derivării
În principiu este necesară alocarea şi dealocarea memoriei pentru înregistrarea adiacenţei, o metodă de precizare a adiacenţei a două vârfuri şi o metodă generală de parcurgere în vederea prelucrării într-o anumită ordine a vârfurilor (prelucrare specificată în clasele derivate):
/* graph.h model minimal de graf, uşor de surclasat ulterior */ #include <vector> typedef std::vector<int> bin; // "dulap" pentru adiacenţi typedef bin::iterator bin_it; // "pointer" de adiacenţi ai vârfului class Graph { bool directed; // orientat sau neorientat public: Graph(int V, bool directed=true): V( V ), adj( new bin[V] ), directed( directed ) {} // constructor ~Graph() { delete [] adj; } // destructor void addEdge(int, int); // adaugă o muchie (sau arc) void to_DOT(const char*); // produce fişier DOT (pentru imagine grafică) void DFS(int, std::vector<bool>&); // Depth-first-search virtual void process(int); // prelucrează din DFS() nodul vizitat protected: int V; // numărul de vârfuri bin *adj; // adj[w] = lista adiacenţilor lui w, w=0..V-1 };
Dacă am prefera <list> în loc de <vector>, atunci vom avea de înlocuit doar în primele două linii.
Am lăsat adj sub "protected" (nu "private"), încât o clasă derivată din Graph va putea seta adiacenţa vârfurilor după caz. Redefinind metoda virtuală process(), vârfurile vor putea fi prelucrate după caz prin apelul la Graph::DFS(); pentru simplitate - n-am prevăzut aici şi o metodă BFS, necesară şi aceasta unor diverse clase derivate.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | /** graph.cpp **/ #include "graph.h" #include <iostream> #include <fstream> void Graph::addEdge(int v, int w) { adj[v].push_back(w); // adaugă w ca adiacent al lui v if(!directed) // (graf neorientat) adj[w].push_back(v); // adaugă v ca adiacent al lui w } // produce un fişier DOT (graph description language) minimal // dot -Tpng -o filename.png filename.dot void Graph::to_DOT(const char* filename) { std::ofstream out(filename); switch(directed) { case true: out << "digraph G {\n"; for(int u=0; u < V; ++u) for(bin_it v = adj[u].begin(); v != adj[u].end(); ++v) out << u << "->" << *v << ";\n"; break; case false: out << "graph G {\n"; for(int u=0; u < V; ++u) for(bin_it v = adj[u].begin(); v != adj[u].end(); ++v) if(u < *v) // înscrie numai u--w (nu şi w--u) out << u << "--" << *v << ";\n"; break; } out << '}'; } // parcurge şi eventual evaluează nodurile, "în adâncime" void Graph::DFS(int v, std::vector<bool>& visited) { visited[v] = true; process(v); // prelucrează după caz nodul curent for (bin_it i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFS(*i, visited); } void Graph::process(int v) { // a redefini după caz, în clasele derivate std::cout << v << " "; } |
Metoda to_DOT() din liniile 14-32 produce un fişier DOT, de transmis unui program utilitar precum dot (sau Graphviz) pentru a obţine o imagine grafică. A cam trebuit să dublăm codul din liniile 19-20 pe liniile 25-26, având de distins între "orientat" şi "neorientat" (evitând testarea "directed==true" la fiecare iterare); în cazul "neorientat", muchia trebuie înscrisă în fişierul DOT o singură dată (altfel, dot va desena muchii duble).
Testarea definiţiei Graph
Putem proceda banal, înscriind într-un fişier matricea sau listele de adiacenţă pentru un graf cu vreo 5 vârfuri - urmând ca programul de testare să-l citească şi să apeleze metoda addEdge() pe fiecare pereche de vârfuri indicate în fişier ca adiacente. Dacă vrem grafuri mai mari, putem proceda mai simplu (nefiind de scris vreun fişier prealabil), generând adiacenţe în mod aleatoriu.
Dar putem imagina şi modalităţi de a obţine grafuri care să fie semnificative dintr-un punct de vedere sau altul; de exemplu, dacă am avea de propus un graf eulerian (în scopul de a exersa algoritmul lui Fleury) - ne-am putea baza pe faptul că un ciclu eulerian este un şir care conţine fiecare număr 0..n-1 sau o singură dată, sau de cel mult un anumit număr de ori, primul termen fiind egal cu ultimul şi astfel încât orice pereche de termeni vecini nu se repetă - graful respectiv fiind G = (V, E) cu V = {0,1,...,n-1} şi [u, v] ∈ E ⇔ u şi v sunt termeni vecini în şirul respectiv.
Desigur, dacă procedăm chiar aşa - adică nu folosim direct şirul corespunzător unui ciclu eulerian al unui graf dat, ci plecăm de la un şir de numere arbitrar - atunci vor fi de încercat diverse reordonări şi inserări de termeni în cadrul şirului (n-am zis că ar fi mai simplu, decât a înscrie adiacenţa într-un fişier, pentru un graf dat); totuşi, pot rezulta şi aspecte interesante (inclusiv, privind organizarea investigării).
Programul următor - de compilat cu g++ graph.cpp graph_test.cpp -o test - consideră un astfel de "şir eulerian" în tabloul euler[] şi constituie Graph()-ul G, în care adiacenţa este dată de perechile de termeni consecutivi în şirul respectiv; în final, se invocă metoda to_DOT() pentru G:
#include "graph.h" using namespace std; int main() { // şir eulerian pe 0..17 (cu 24 perechi de termeni vecini) int euler[] = {0, 1, 3, 2, 10, 11, 5, 6, 3, 4, 7, 6, 12, 11, 14, 15, 7, 8, 17, 16, 14, 13, 10, 9, 0}; Graph G(18, false); // construieşte un graf neorientat // setează adiacenţa conform şirului eulerian dat for(int i=0; i < 24; ++i) G.addEdge( euler[i], euler[i+1] ); G.to_DOT("euler.dot"); // obţine fişierul DOT }
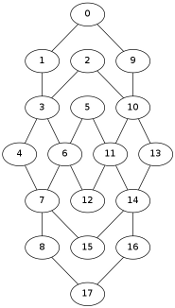
Imaginea din dreapta reprezintă fişierul PNG furnizat de dot pentru fişierul euler.dot obţinut:
vb@vb:~$ dot -Tpng -o euler.png euler.dot
Graful redat - cu 6 noduri de grad 4 şi restul, de grad 2 - este izomorf unui graf dat de trei pătrate care îşi intersectează câte două laturi; nodurile de grad 4 reprezintă intersecţiile de câte două laturi, iar celelelte 12 sunt vârfurile pătratelor. La ThreeSquares este redat un caz particular, cu 5 noduri de grad 4 (două dintre pătrate au un vârf comun şi nu se mai intersectează) şi 10 de grad 2.
Derivarea unor grafuri De Bruijn
În [1] am introdus pe $Z_{2^n}$ relaţia $u\succcurlyeq v$: primii n-1 biţi ai lui $v$ (de la stânga spre dreapta) coincid cu ultimii n-1 biţi ai lui $u$ (n $\geqslant$ 2) şi am demonstrat că $Z_{2^n}$ poate fi parcursă liniar, plecând de la $2^n-1$ şi trecând de la un număr la altul prin intermediul acestei relaţii. Am mai observat că aceasta este echivalentă cu parcurgerea "în adâncime" (plecând din vârful $2^n-1$) a grafului relaţiei respective, $\mathbb{B}_n=(\mathbb{Z}_{2^n},\mathsf{E})$ cu $(u,v)\in\mathsf{E}\Leftrightarrow u\succcurlyeq v$ (caz particular de graf De Bruijn).
Putem modela grafurile $\mathbb{B}_n$ (şi problemele din [1]) plecând de la clasa Graph, astfel:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | /** bgraph.h graf De Bruijn peste {0,1}, derivat din Graph **/ #include "graph.h" #include <cmath> // pow() class Bgraph: public Graph { public: Bgraph(int n): Graph(pow(2, n)) { bruijn_link(); } ~Bgraph() {} void process(int); // Graf::DFS() apelează această metodă void print_DFS(); void bruijn_print(); private: bin DFS_tour; // nodurile în ordinea vizitării DFS() void bruijn_link(); // construieşte adiacenţa dată de "înlănţuire" }; |
În linia 7 se prevede extinderea unui obiect Graph (cu $2^n$ vârfuri) prin invocarea metodei private specificate în linia 17, menite să instituie adiacenţa conformă cu relaţia $\succcurlyeq$ din $\mathbb{Z}_{2^n}$.
Metoda Graph::process() va fi rescrisă (linia 10), astfel încât traseul Graph::DFS() să fie înregistrat în containerul DFS_tour din linia 16; liniile 12-13 specifică acele metode utilitare care declanşează DFS($2^n-1$) şi afişează şirul De Bruijn rezultat în DFS_tour, deducând şi afişând deasemenea şi reprezentarea binară minimală a acestuia.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | /** bgraph.cpp **/ #include "bgraph.h" #include <iostream> void Bgraph::bruijn_link() { int m = V >> 1; // se obţine $2^{n-1}$ for(int u=0; u < V; ++u) { int v = 2*(u % m); // avem $u\succcurlyeq v$ şi $u\succcurlyeq (v+1)$ adj[u].push_back(v); adj[u].push_back(v+1); } } void Bgraph::process(int v) { // redefineşte metoda virtuală Graph::process() DFS_tour.push_back(v); // consemnează nodul curent vizitat de DFS() } void Bgraph::print_DFS() { int n = log2(V); // V = $2^n$ std::string seq(n-1, '1'); // începe cu n-1 biţi 1 for(bin_it i=DFS_tour.begin(); i != DFS_tour.end(); ++i) { std::cout << *i << " "; // resturile MOD $2^n$, ordonate de "înlănţuire" seq += (*i & 1? '1':'0'); // anexează bitul de paritate } std::cout << '\t' << seq << '\n'; // reprezentarea binală minimală pentru $\mathbb{Z_{2^n}}$ } void Bgraph::bruijn_print() { std::vector<bool> visited(V, false); // marchează vârfurile ca nevizitate DFS(V-1, visited); // traversează liniar $\mathbb{B_n}$, din vârful $2^n-1$ print_DFS(); } |
Trebuie observat că dacă nu aveam grijă să declarăm virtual process() în fişierul "graph.h" - atunci apelul DFS() (metodă a clasei Graph) din linia 27 ar fi folosit Graph::process(), nu Bgraph::process() şi nu mai obţineam popularea lui DFS_tour şi deci, nici rezultatele aşteptate.
Exemplificăm folosirea clasei create mai sus, prin următorul program (a cărui compilare va trebui să decurgă după modelul g++ graph.cpp bgraph.cpp btest.cpp -o btest):
#include "bgraph.h" #include <cstdlib> using namespace std; int main(int argc, char** argv) { int n = argc > 1? atoi(argv[1]):3; Bgraph B(n); B.to_DOT("bruijn.dot"); B.bruijn_print(); }
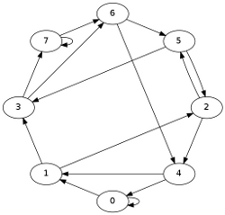
Imaginea alăturată reprezintă graful $\mathbb{B}_3$ (după invocarea dot -Tpng -Kcirco bruijn-3.png bruijn.dot); iată două rezultate de execuţie a programului:
vb@vb:~$ ./btest 7 6 4 0 1 2 5 3 1110001011 vb@vb:~$ ./btest 4 15 14 12 8 0 1 2 4 9 3 6 13 10 5 11 7 1111000010011010111
Şirurile afişate sunt valorile din $\mathbb{Z}_8$ şi respectiv $\mathbb{Z}_{16}$, obţinute în DFS_tour prin apelarea DFS(7) şi respectiv DFS(15), ordonate (cum am arătat în [1]) de relaţia $\succcurlyeq$; secvenţele binare afişate constituie cuvinte binare minimale care conţin drept subcuvinte toate valorile (în reprezentare binară) din şirul respectiv.
Desigur, putem proceda ca mai sus (derivând din clasa Graph) în diverse alte cazuri. De exemplu, dacă vrem un drum al calului pe o tabla de şah $n\times n$: creem o clasă derivată din Graph al cărei constructor să seteze adiacenţa dată de săritura calului şi care să conţină un câmp privat analog cu "DFS-tour", în care să fie înscris drumul hamiltonian respectiv; metoda care mai trebuie adăugată, de căutare a drumului conform adiacenţei constituite - va putea folosi Graph::DFS().
vezi Cărţile mele (de programare)