În general, transformarea Nf(z) = z - f(z) / f'(z) asociată unei funcţii derivabile f(), produce şiruri zn+1 = N(zn) care - exceptând anumite valori iniţiale - converg la una dintre rădăcinile lui f() (altfel spus, rădăcinile lui f() sunt punctele fixe al lui Nf()). Ilustrăm două astfel de şiruri de puncte; am evidenţiat cu roşu primul şi ultimul termen şi am gradat culoarea indecşilor pentru ceilalţi:

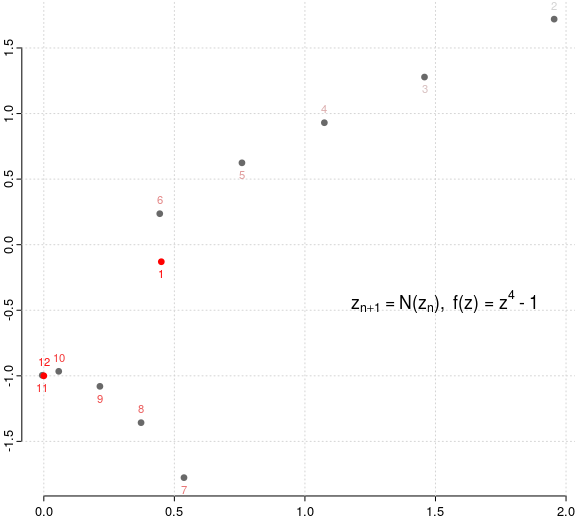
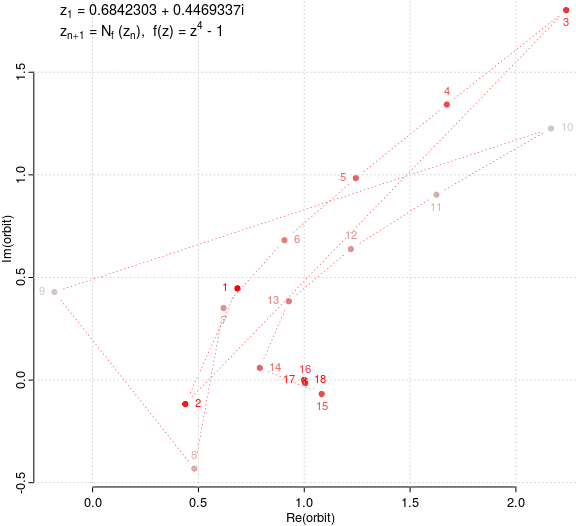
După 12 şi respectiv 18 iteraţii, punctele redate se apropie suficient de mult de rădăcinile -i ≡ (0, -1) şi respectiv 1 ≡ (1, 0), ale polinomului de variabilă complexă z4 - 1; pentru acest polinom am constatat experimental că şirurile care pleacă de la puncte ale bisectoarelor y = ±x nu sunt convergente, ci oscilează indefinit - oricât am mări numărul de iteraţii - pe bisectoarea respectivă (având totuşi tendinţa de a se apropia periodic de punctul iniţial; însă nu vom putem avea concluzii ferme operând într-un program, cu un model aproximativ pentru numerele "reale"…).

Mai departe - corectând faţă de [1] anumite aspecte - considerăm rădăcinile de ordinul n ale unităţii (deci rădăcinile polinomului zn - 1), punctele unui pătrat care include cercul unitate şi - prin parametrul "kol" al funcţiei attract() - fixăm un vector de culori (de dorit, câte una pentru fiecare dintre cele n rădăcini); aplicăm fiecărui punct transformarea menţionată mai sus şi-l colorăm după rădăcina atractoare, gradând eventual după numărul de iteraţii necesar:

attract <- function(n=4, tip = 1, 
                    x = seq(-1.3, 1.3, length=800), 
                    kol=c("black", "#67001f", "#7f2704", "#08306b")) {
  roots <- exp(1i * 2*pi * (0:(n-1)/n))  # rădăcinile de ordinul n ale unităţii
  eps <- 1E-8
  ## ramps() -> matrice (coloana j: 32 nuanţe spre "NA" ale culorii rădăcinii a j-a)
  ramps <- function() {
    return(sapply(seq_along(roots), function(id) 
                  colorRampPalette(c(kol[id], "NA"))(32)))
  }
  ## rmatch() -> indexul rădăcinii spre care tinde orbita (sau 0)
  rmatch <- function(u) {
    for(id in seq_along(roots)) {
      if(abs(u - roots[id]) < eps) return(id)
    }
    return(0)
  }
  ## orbiting(): orbitează din z0 (metoda lui Newton), returnând - ca număr complex -
  ## lungimea orbitei şi indexul rădăcinii atractoare (sau 0, după 100 iteraţii)
  orbiting <- function(z0) {
    for(it in 1:100) {
      z1 <- ((n - 1)*z0 + z0^(1-n)) / n  # x - f(x)/f'(x) pentru f(x) = x^n - 1
      if(abs(z1 - z0) < eps) {
        id <- rmatch(z1)  # indexul rădăcinii atractoare
        return(id + 1i*it)
      }
      z0 <- z1  # continuă orbitarea, din punctul z1
    }
    return(0)  # dacă nu atinge o rădăcină, nici după 100 de iteraţii
  }
  ## constituie vectorul afixelor punctelor pânzei, orbitează din fiecare şi colorează
  Z <- c(outer(x, x, function(u, v) u + 1i*v))
  switch(tip,
    { # 1: colorează punctele după culoarea rădăcinii atractoare
      q <- sapply(Z, orbiting)
      plot(Z, col=Re(q), cex=0.2, pch=19)
    },
    { # 2: colorează punctele după lungimea orbitelor corespunzătoare
      q <- sapply(Z, orbiting)
      plot(Z, col=Im(q), cex=0.2, pch=19)
      # plot(z, col=round(4*log10(Im(q))+1), cex=0.2, pch=19)  # (Varianta 1)
      # pal <- randomcoloR::distinctColorPalette(17)
      # plot(z, col=pal[round(8*log10(Im(q))+1)], cex=0.2, pch=19)  # (Varianta 2)
    },
    { # 3: colorează după atractori, gradând după lungimile orbitelor
      ramp <- ramps()
      q <- sapply(sapply(Z, orbiting), function(k) 
                  ifelse(Re(k) > 0, ramp[round(15*log10(Im(k)))+1, Re(k)], "NA"))
      plot(Z, col=q, cex=0.2, pch=19)
    }
  )
}

Tot în contextul funcţiei attract(), în [1] defineam funcţia orbiting() în trei variante, dintre care (prin switch(tip)) se executa cea corespunzătoare valorii găsite în parametrul "tip" - interpretând astfel, ideea de "funcţie generică" (de exemplu, funcţia plot() are multe "variante", dintre care la execuţie se alege aceea care corespunde obiectului de plotat: plot(sin, 0, 2*pi) va lansa metoda plot.function() pentru a trasa graficul funcţiei; plot(rast) va lansa metoda plot.raster(), dacă "rast" este un obiect de tip "raster" - v. [2]; plot(hst) va lansa plot.histogram(), dacă "hst" este structura de date returnată anterior de funcţia hist() - etc.).

Acum (renunţând la artificii de programare), am formulat orbiting() în maniera tipică proceselor iterative: se transformă punctul curent (începând cu cel primit ca parametru) până ce fie că acesta şi transformatul său diferă suficient de puţin, fie se depăşeşte numărul maxim admis de iteraţii; se returnează nu culoarea de asociat punctului iniţial (cum aveam - defectuos - în [1]), ci un număr complex conţinând indexul rădăcinii atractoare şi numărul de iteraţii efectuate.

În formularea din [1] decideam continuarea orbitei calculând apropierea ultimului punct al ei faţă de rădăcinile atractoare; acum am procedat mult mai simplu, ţinând seama de observaţia făcută la început "rădăcinile lui f() sunt punctele fixe al lui Nf()": încheiem când distanţa dintre punct şi transformatul acestuia este suficient de mică (sau se depăşeşte maximul de iteraţii stabilit).

Funcţia attract() constituie vectorul "Z" al afixelor punctelor pătratului şi aplică acestuia funcţia orbiting() - rezultând vectorul complex "q", în care q[i] are ca parte reală culoarea rădăcinii atractoare (sau o anumită nuanţă a acesteia) şi ca parte imaginară, numărul de iteraţii făcute plecând de la punctul Z[i] (pe datele textului-sursă de mai sus, lungimea lui Z este 800*800).

În final, se plotează punctele din Z - fie în culoarea Re(q) (deci, în culoarea atractorului), fie în culoarea Im(q) (deci, după numărul de iteraţii), fie - în cazul când s-a apelat cu tip = 3 - prin acea nuanţă a culorii atractorului corespunzătoare numărului de iteraţii, dintre cele câte 32 de nuanţe spre "NA" stabilite prin funcţia ramps().

Pentru acest din urmă caz, am avut în vedere că a colora nuanţat după numărul de iteraţii ar însemna - strict vorbind - să folosim câte 100 de nuanţe (pentru fiecare atractor); am preferat desigur, să colorăm după valorile 15*log10(Im(k)) (scalarea cu 15 asigurând indicii de culoare 1..32 prevăzuţi în ramps()).

Ar mai fi de precizat că în cazul când în parametrul "col" al funcţiei plot() este transmis un vector de întregi - cum avem aici pentru tip = 1 şi pentru tip = 2 - acesta este interpretat ca index în paleta de culori din sesiunea R curentă; ca urmare, dacă n > 8 atunci măcar doi atractori (şi punctele atrase) vor avea o aceeaşi culoare (paleta implicită având numai 8 culori) - iar pentru a preveni aceasta, trebuie ca în prealabil să se indice prin palette() un număr de n culori.

Pentru tip = 2 puteam alege să colorăm analog cazului tip = 3, aducând indecşii de culoare de exemplu între 1 şi 8, prin 4*log10(Im(k)) + 1 (variantă adăugată drept comentariu, în programul redat mai sus); sau şi mai bine (comentariul "Varianta 2") - puteam institui un set de 16 culori contrastante şi să indexăm în acest set (prin 8*log10(Im(k)) + 1).

Desigur… în loc de a prevedea drept "comentariu" aceste variante, era mai mult mai bine să regândim parametrul "kol", care în programul redat este folosit numai în cadrul funcţiei ramps(); puteam prevedea să transmitem prin "kol" culorile necesare unuia sau altuia dintre cazuri, de exemplu cele 16 "culori contrastante" de care vorbeam mai sus.

Rezultatele sunt asemănătoare celor obţinute în [1], dar timpul de execuţie - deşi acum nu am mai folosit compiler::enableJIT(3) - s-a redus cam cu 50% (ajungând la 20-30 secunde):

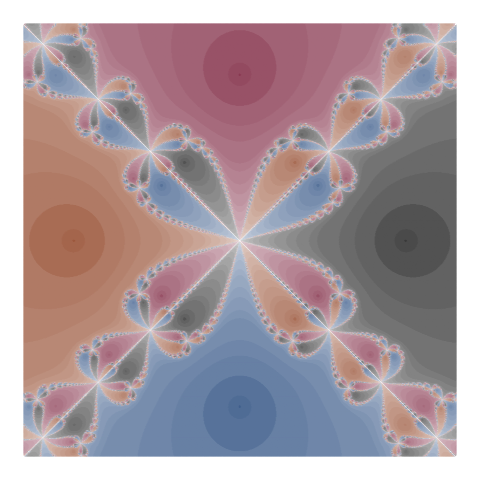
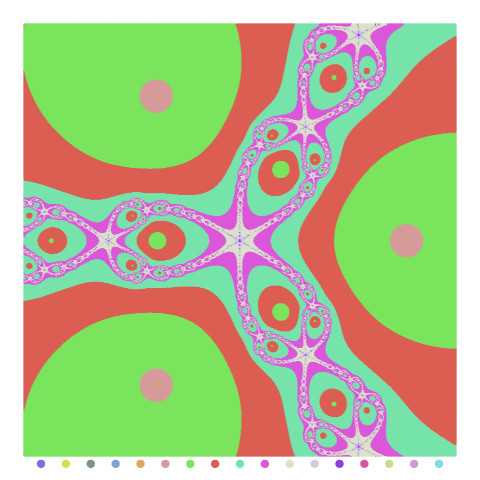
Doar prima imagine (pentru "tip = 3"), ar marca o îmbunătăţire faţă de [1]: culorile asociate rădăcinilor atractoare sunt degradate după treptele descrescătoare ale vitezei cu care sunt atrase punctele; culoarea neutră (alb) de pe diagonale ar spune că punctele acestora nu sunt atrase de niciuna dintre rădăcini (cel puţin pentru numărul maxim de iteraţii implicat). Este de observat că şi puncte de pe conturul fiecărei "frunze" sunt albe - însemnând poate, că şi acestea sunt în afara bazinelor de atracţie ale rădăcinilor…

Pe celelalte două imagini (cu "tip = 2"), fiecare culoare marchează punctele care orbitează spre o rădăcină cam cu aceeaşi viteză, dar fără a diferenţia faţă de ordinul de mărime al numărului de iteraţii; în a treia imagine avem totuşi o încercare (nu tocmai reuşită) de a indica această ordine: la baza imaginii am adăugat puncte colorate după o gamă crescătoare a numărului de iteraţii.

Am strecura acum o mică dezvăluire, vizând o anumită manieră de lucru; ştiam de la bun început ce facem, prezentând în mod critic programul "imperfect" de mai sus şi rezultate care lasă de dorit ale acestuia (marcând diverse aspecte defectuoase, sau "periind" când a fost cazul, în raport cu [1]): gândim pe cât putem şi încropim mereu reluarea ulterioară a lucrurilor.