Studiul datelor examenului de bacalaureat din 2016 (folosind R)
Pe la sfârşitul lui august 2016 s-au postat pe data.gov.ro rezultatele examenului de bacalaureat, atât în format ODS, cât şi în format CSV. Bineînţeles că nici nu m-am uitat la "ODS" - a vedea [1] - şi am descărcat fişierul "2016sesiuneai.csv", cu intenţia de a relua analiza din [1].
Inspectând în hexazecimal fişierul respectiv, am constatat imediat că de această dată s-a folosit codificarea UTF-8 (în loc de UTF-16 - v. [1]); ca separator de câmpuri s-a folosit virgula (în loc de "TAB", ca în cazul vizat în [1]) - numai că s-a folosit greşit: în coloana "Medie" apar numere întregi ca 88, 46, etc. (ceea ce este absurd, fiindcă mediile de examen sunt între 5 şi 10 şi pot fi cu zecimale, de exemplu 7.56). Prin urmare, s-a înlocuit "TAB" cu "," - dar s-a păstrat virgula şi în cadrul mediilor (în loc să fi înlocuit-o în prealabil, cu "."); astfel, media 7.56 a rămas înscrisă ca 7,56 şi fiindcă s-a optat pentru separarea câmpurilor prin virgulă - ea a fost "separată" în două câmpuri (întregi): 7 şi 56.
Dar n-a fost nevoie să caut vreun algoritm de corectare: deschizând în LibreOffice Calc fişierul celălalt, "2016sesiuneai.ods" - am constatat că valorile câmpului "Medie" sunt corecte (şi încă, separând zecimalele de partea întreagă chiar prin ".", nu prin ','); aşa că am folosit opţiunea de meniu "Save As..." şi am obţinut fişierul CSV corect - numit "bac16.csv". Mai mult - inspectând iarăşi în hexazecimal, am constatat că sfârşitul de linie are codul 0x0A (şi nu 0x0D0A, ca pe un sistem DOS) semn că LibreOffice - fiind pe Linux - a salvat cu "end-line" specific Linux.
Prin urmare, pentru "bac16.csv" nu mai sunt de făcut transformările prealabile arătate în [1] (de la UTF-16 la UTF-8, înlocuirea virgulei cu punct în reprezentările zecimale, reducerea codului 0x0D0A la 0x0A şi eventual, înlocuirea caracterului "TAB" cu virgulă).
Lansăm R şi creem un obiect "data.frame" pentru datele din fişierul respectiv:
vb@Home:~/16_bac$ R -q # --quiet (omite mesajul introductiv) > bac6 <- read.csv("bac16.csv") > str(bac6) # inspectăm structura de date creată 'data.frame': 137338 obs. of 52 variables: # aceleaşi 52 de variabile ca în 'bac5' din [1]
Deci avem 137338 candidaţi (faţă de 168939 câţi au fost în 2015). Constatând că avem exact aceleaşi coloane de date (şi în aceeaşi ordine) ca în structura de date "bac5" din [1] - am putea să imităm întru totul analiza din [1] (înlocuind "bac5" cu "bac6" şi făcând în plus doar comparaţiile care se cuvin, între acestea).
Dar se cuvine să fim atenţi: denumirile coloanelor au rămas aceleaşi (inclusiv, "Fileira"), însă în multe cazuri (nu neapărat importante) semnificaţia este îmbogăţită; mai precis - mai multor variabile de clasă "factor" le-au fost adăugate noi niveluri. Cel mai banal exemplu este câmpul "Promoţie", la care fireşte că acum apare şi nivelul "2014-2015"; iar cele cinci câmpuri pe care se înregistrează nivelul competenţelor lingvistice au acum câte 6 niveluri (în [1] găseam 5):
levels(bac6$ITA) # nivelurile variabilei "Înţelegerea Textului Audiat" [1] "-" "A1" "A2" "B1" "B2" "Neevaluat"
Pe de altă parte, în [1] am cam exagerat cu simplificările; de exemplu, acolo (în &6 "Notele finale versus instituţia contestaţiei") ignoram notele acordate în urma soluţionării contestaţiilor, dar în final (cam târziu) constatam că ar fi interesant de comparat densitatea repartiţiei mediilor finale, cu cea corespunzătoare situaţiei dinaintea rezolvării contestaţiilor.
1. Familiarizarea cu datele existente; simplificări
Analiza unui set de date trebuie pornită de la înţelegerea prealabilă a datelor cu care ai de-a face; chiar şi dacă eşti familiarizat cu ele, tot e bine să revezi lucrurile.
Să afişăm o înregistrare oarecare, dar într-o formă lizibilă. Avem 52 de coloane, conţinând fie text, fie numere; nu este convenabilă nici afişarea pe linie, nici afişarea valorilor respective pe o singură coloană - vrem ca toate datele respective să încapă într-un ecran obişnuit, evitând pe cât se poate, operaţii de derulare (prin bare suplimentare de "scroll").
Această problemă de lizibilitate a reprezentării datelor apare frecvent. De obicei ea este trecută sub tăcere, afişând datele respective într-o diviziune de ecran prevăzută cu bare de "scroll" - dar această "soluţie" este valabilă (să zicem) numai pentru accesarea datelor printr-o aplicaţie de tip "browser"; în [1] de exemplu, am folosit de mai multe ori, această soluţie - ajungând în impas în cursul transformării în format PDF (prin meniul "Print..." al browserului) a paginii HTML respective: barele de "scoll" apar şi în PDF - numai că pe o imagine (tipărită eventual pe hârtie) nu poţi folosi mouse-ul, ca să derulezi caseta respectivă.
Putem rezolva chestiunea introducând o structură auxiliară de date, în care copiem numele de coloane şi valorile din coloanele respective de pe linia de date indicată, pentru primele 26 şi apoi la fel pentru următoarele 26 de coloane:
tst <- t(bac6[sample(1:nrow(bac6), 1), ]) # selectează aleatoriu o linie şi o transpune nume <- row.names(tst) # de fapt, numele coloanelor din "bac6" # indexul coloanei (din "bac6"), numele coloanei, valoarea din acea coloană pe linia indicată: tst.df <- data.frame(id1 = 1:26, nume1 = nume[1:26], values1 = tst[1:26], id2 = 27:52, nume2 = nume[27:52], values2 = tst[27:52]) print(tst.df, row.names = FALSE) id1 nume1 values1 id2 nume2 values2 1 Cod.unic.candidat 442158 27 STATUS_C Calificativ 2 Sex M 28 STATUS_D Experimentat 3 Specializare Matematica-Informatica 29 STATUS_EA Promovat 4 Profil Real 30 STATUS_EB Neevaluat 5 Fileira Teoretica 31 STATUS_EC Promovat 6 Forma.de.învățământ Zi 32 STATUS_ED Promovat 7 Mediu.candidat URBAN 33 ITA B2 8 Unitate..SIIIR. 361104588 34 SCRIS_ITC B1 9 Unitate..SIRUES. 336037 35 SCRIS_PMS A1 10 Clasa a XII-a B M-I 36 ORAL_PMO B1 11 Subiect.ea Limba română (REAL) 37 ORAL_IO B1 12 Subiect.eb 38 NOTA_EA 7.65 13 Limba.modernă Limba engleză 39 NOTA_EB <NA> 14 Subiect.ec Matematică MATE-INFO 40 NOTA_EC 8.6 15 Subiect.ed Fizică TEO 41 NOTA_ED 7.15 16 Promoție 2015-2016 42 CONTESTATIE_EA Da 17 NOTE_RECUN_A Nu 43 NOTA_CONTESTATIE_EA 8.4 18 NOTE_RECUN_B Nu 44 CONTESTATIE_EB Nu 19 NOTE_RECUN_C Nu 45 NOTA_CONTESTATIE_EB <NA> 20 NOTE_RECUN_D Nu 46 CONTESTATIE_EC Nu 21 NOTE_RECUN_EA Nu 47 NOTA_CONTESTATIE_EC <NA> 22 NOTE_RECUN_EB Nu 48 CONTESTATIE_ED Nu 23 NOTE_RECUN_EC Nu 49 NOTA_CONTESTATIE_ED <NA> 24 NOTE_RECUN_ED Nu 50 PUNCTAJ.DIGITALE 88 25 STATUS_A Experimentat 51 STATUS Promovat 26 STATUS_B Neevaluat 52 Medie 8.05
În continuare ne referim la datele expuse mai sus şi vrem să vedem ce denumiri schimbăm (cu siguranţă, vom corecta numele coloanei de index 5), la care coloane putem renunţa şi ce noi coloane - sau "variabile", cum se zice de regulă în R - ar fi utile.
Analiza pe care ne-o propunem merge până la nivelul de judeţ - prin urmare putem renunţa la coloanele 8, 9 şi 10 (care ne-ar permite să identificăm şi şcolile de care aparţin candidaţii, ba chiar şi clasele în care au fost aceştia). Să înfiinţăm în schimb, o coloană 'jud' în care să indicăm judeţul de care aparţine fiecare candidat.
Avem 42 de "judeţe", codificate în mod standard prin câte două cifre. Codul SIIIR din coloana 8 are nouă sau zece cifre - prima, respectiv primele două, reprezentând codul judeţului; de pildă, înregistrarea redată mai sus are 9 cifre în coloana 8, iar prima cifră 3 indică judeţul de cod "03" - anume Argeş. Funcţia jud_from_siiir() din [1] §5.1 returnează prima cifră prefixată cu "0", sau primele două cifre din codul de 9, respectiv 10 cifre primit ca argument şi ne serveşte pentru a înfiinţa coloana 'jud', conţinând deocamdată codurile de câte două cifre ale judeţelor de care aparţin candidaţii (valori de tip "character"):
bac6$jud <- jud_from_siiir(bac6[[8]]) # codul "NN" al judeţului candidatului col_to_remove <- c(8:10) # reţine coloanele pe care în final le vom elimina
Nu ştergem deocamdată, coloanele respective - păstrându-ne posibilitatea de a le referi şi în continuare prin indecşii din "id1" şi "id2" din tabelul de date redat mai sus (prin ştergerea unei coloane, indecşii respectivi s-ar modifica).
Transformăm 'jud' în variabilă de clasă "factor" şi-i înscriem ca niveluri, nivelurile factorului 'jud' existent în "bac5" din [1] (avem astfel denumirile judeţelor, în locul codurilor de câte două cifre):
bac6$jud <- as.factor(bac6$jud) load("../15_bac/bac5.RData") # recuperează 'bac5', pentru nivelurile factorului 'jud' levels(bac6$jud) <- levels(bac5$jud) rm(bac5) # elimină 'bac5' din sesiunea de lucru curentă (rm() = "remove")
Coloanele 17..24 indică prin "Da" sau "Nu" recunoaşterea sau nu, a uneia sau alteia dintre notele sau calificativele acordate într-o sesiune de bacalaureat anterioară - note şi calificative care, indiferent de caz, sunt înscrise în coloanele 38..41 şi respectiv, 29..32. Credem că "Da" are o proporţie foarte mică (din câte ştim, marea majoritate a candidaţilor este formată din absolvenţii ultimei promoţii - iar pentru aceştia recunoaşterea sau nu a rezultatelor din sesiuni anterioare nu are sens); dar - înainte de a elimina coloanele respective - să facem totuşi, o verificare:
summary(bac6[17:24]) NOTE_RECUN_A __B __C __D __EA __EB __EC __ED Da: 21145 Da: 857 Da: 30557 Da: 32695 Da: 13383 Da: 735 Da: 11499 Da: 9892 Nu:116193 Nu:136481 Nu:106781 Nu:104643 Nu:123955 Nu:136603 Nu:125839 Nu:127446
Surpriză, desigur… La probele D şi C avem un număr mare de valori "Da" (câte peste 20% din totalul candidaţilor). Aceasta ar însemna că va trebui - spre deosebire de [1], unde nu luasem seama la acest aspect - să vizăm separat cazul ultimei promoţii de absolvenţi şi respectiv, al acelora proveniţi din promoţii anterioare.
Coloanele respective nu ne mai pot spune şi altceva, încât le colectăm pentru ştergere; de asemenea, vom renunţa la coloanele "Da/Nu" care spun dacă elevul a depus sau nu cerere de contestare la una sau alta dintre probe (dar - spre deosebire de [1] - păstrăm coloanele în care se consemnează notele acordate în urma soluţionării eventualelor contestaţii):
append(col_to_remove, c(17:24, seq(42, 48, by=2))) -> col_to_remove
Ne atrăgeam atenţia mai înainte, asupra seriilor anterioare; să vedem exact situaţia acestora, folosind iarăşi summary(), pentru variabila de clasă factor 'Promoție' (transformăm în data.frame, pentru lizibilitate):
as.data.frame(summary(bac6$Promoție)) summary(bac6$Promoție) 19XY 128 # din serii anterioare anului 2000 2000-2001 15 2001-2002 17 2002-2003 20 2003-2004 23 2004-2005 17 2005-2006 31 2006-2007 33 2007-2008 77 2008-2009 120 2009-2010 518 2010-2011 1296 2011-2012 1974 2012-2013 3198 2013-2014 4451 2014-2015 10442 2015-2016 114978 sum(.Last.value[-17, ]) [1] 22360 # total candidaţi din seriile anterioare ultimei promoţii
În general, funcţiile invocate din consola R au în mod implicit efectul lateral de afişare a rezultatului, dacă acesta nu este explicit atribuit unei variabile - iar dacă n-am folosit şi un operator de atribuire, atunci rezultatul (odată expus) pare "pierdut". După ce am lansat comanda de sumarizare (fără a specifica o variabilă care să păstreze rezultatul) şi am văzut pe ecran rezultatul redat mai sus - am vrut să vedem câţi elevi avem în total, din seriile precedente; putem încă accesa rezultatul tocmai afişat, folosind variabila internă '.Last.value' (aceasta păstrează valoarea ultimei expresii evaluate).
Acum chiar avem o surpriză: constatarea că avem numai 22360 candidaţi din seriile anterioare celei curente nu se corelează deloc cu interpretarea de mai sus a numărului de 32695 valori "Da" pentru "NOTE_RECUN_D" (ziceam că acestea reprezintă note transferate din sesiunile anterioare ale examenului); diferenţa fiind aşa de mare - este clar că mi-a scăpat vreun aspect normativ. Într-adevăr: revăzând diverse reglementări în vigoare pentru examenul de bacalaureat - am înţeles în sfârşit că "NOTE_RECUN_ " vizează nu numai rezultatele obţinute în sesiunile anterioare, dar şi rezultate obţinute (inclusiv de către absolvenţi ai seriei curente) în diverse concursuri sau atestări oficiale prealabile examenului de bacalaureat.
Din fericire, nu este cazul să revenim asupra coloanelor "NOTE_RECUN_ " (menţinem decizia de a le şterge). Să observăm că 22360 înseamnă 16.28% din totalul candidaţilor; aproape jumătate dintre aceşti 16.28% sunt din seria "2014-2015", iar la seriile anterioare acesteia valorile sunt mult mai mici. Ni se pare absolut rezonabil să reducem nivelurile factorului "Promoţie" la două - unul corespunzător seriei curente şi unul asociat tuturor celorlalţi 16.28%:
levels(bac6$Promoție)[1:16] <- "OTHER" as.data.frame(summary(bac6$Promoție)) OTHER 22360 # candidaţi din alte promoţii 2015-2016 114978
Pe al treilea câmp, 'Specializare' avem 97 de niveluri, dintre care (cum ştim din [1] §8) două sunt redundante şi le comasăm:
levels(bac6[[3]])[14:15] # inspectează specializările 14 şi 15 (nu sunt ele identice?) [1] "Matematica-informatica" "Matematica-Informatica" levels(bac5[[3]])[14:15] <- "Matematică-Informatică" # comasează şi redenumeşte
Să vedem ca şi în [1], ce ar fi de spus despre aceste 96 de "specializări":
table(bac6[[3]]) -> spec # frecvenţa specializărilor subset( as.data.frame(spec), Freq >= 1000 ) -> spec1 cat( nrow(spec1), " specializări = ", sum(spec1[, 2])/nrow(bac6), "%\n" ) 23 specializări = 0.8757518%
Numai la 23 dintre cele 96 de specializări, avem mai mult de câte 1000 de candidaţi - cumulând 87.58% din totalul candidaţilor; principial vorbind, sunt mult prea multe "specializări" (marea majoritate a candidaţilor acoperă abia un sfert dintre specializări; la unele dintre acestea - vreo 40 - avem câte sub 100 de candidaţi). Ordonăm descrescător după frecvenţe şi redăm situaţia pentru primele 6 specializări:
spec[order(-spec$Freq), ][1:6, ] # în ordinea descrescătoare a frecvenţelor Var1 Freq 14 Matematică-Informatică 25549 # 18.6% din totalul candidaţilor 9 Filologie 21858 # 15.9% 19 Științe ale Naturii 17900 20 Științe Sociale 10679 43 Tehnician în activități economice 9646 # 7.02% 13 Liceu cu program sportiv 3898 # 2.84%
Ultima specializare în ordinea indicată mai sus pentru care Freq > 1000 este "Tehnician proiectant CAD", având Freq=1076; urmează "Teologie Ortodoxă", cu Freq=861 ş.a.m.d. până la specializările "Tehnician veterinar pentru animale de companie", cu Freq=7, "Teologie Musulmană cu Freq=2, ş.a.m.d. În raport cu masa candidaţilor, 1000 este deja nesemnificativ (însemnând 0.7%) - aşa că ni se pare firesc să unificăm nivelurile factorului 'Specializare' la care numărul corespunzător de candidaţi este sub 1000:
spec[order(-spec$Freq), ] -> spec levels(bac6[[3]])[spec$Freq < 1000] <- "OTHER" # 49167 candidaţi au alte specializări ("OTHER") decât cele mai frecvente 23
Denumirile câmpurilor nu sunt neapărat, importante; putem totdeauna folosi operatorul "[[]]" pentru a accesa o coloană de date prin indexul ei (de exemplu, bac6[[3]] returnează vectorul constituit din valorile existente în coloana "Specializare" - cu precizarea că acest vector poate fi obţinut şi prin bac6$Specializare). Dar când coloana respectivă este implicată în diverse vizualizări grafice, numele folosit devine important (de exemplu, nu-i de dorit să fie unul lung şi nici să fie scris cu majuscule). Noi modificăm majoritatea denumirilor, astfel:
names(bac6)[c(1,5:7, 11:15, 25:32, 34:41, 43, 45, 47, 49, 50, 51)] <- c( "id", "Filiera", "Forma_inv", "Mediu", "sub_EA", "sub_EB", "Limba", "sub_EC", "sub_ED", "status_A", "status_B", "status_C", "status_D", "status_EA", "status_EB", "status_EC", "status_ED", "ITC", "PMS", "PMO", "IO", "nota_EA", "nota_EB", "nota_EC", "nota_ED", "nota_cEA", "nota_cEB", "nota_cEC", "nota_cED", "pDIGI", "status")
Acum putem elimina coloanele pe care le-am marcat anterior în vectorul "col_to_remove":
bac6[, col_to_remove] <- NULL
Imaginea următoare prezintă în două panouri (copii de porţiuni de ecran - din consola R - reunite orizontal prin programul "montage" din pachetul ImageMagick) structura finală a datelor din "bac6" (am preferat aşa de data aceasta, fiindcă totuşi - imaginea este mai "concisă" decât textul redat pe ecran prin comanda str(bac6)):
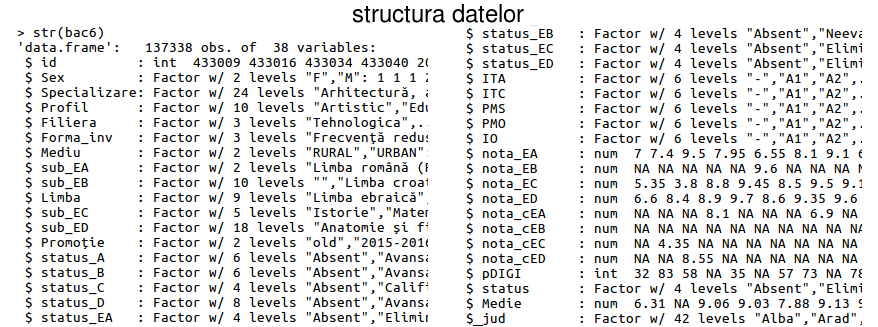
În final, "bac6" conţine 38 de coloane (sau variabile), ocupând în memorie aproape 25 MB:
print(object.size(bac6), units = "MB") [1] "24.7 Mb"
Putem începe acum să investigăm "ce spun" datele respective; o să avem nevoie mereu, de numele şi indecşii câmpurilor şi le reţinem aici:
names(bac6) [1] "id" "Sex" "Specializare" "Profil" "Filiera" [6] "Forma_inv" "Mediu" "sub_EA" "sub_EB" "Limba" [11] "sub_EC" "sub_ED" "Promoție" "status_A" "status_B" [16] "status_C" "status_D" "status_EA" "status_EB" "status_EC" [21] "status_ED" "ITA" "ITC" "PMS" "PMO" [26] "IO" "nota_EA" "nota_EB" "nota_EC" "nota_ED" [31] "nota_cEA" "nota_cEB" "nota_cEC" "nota_cED" "pDIGI" [36] "status" "Medie" "jud"
2. Diferenţierea filierelor
Ne întrebăm întâi dacă există diferenţe majore între filiere.
Bineînţeles - alde noi nu ne putem abţine să nu corectăm întâi, denumirile:
levels(bac6[[5]]) # Filiere [1] "Tehnologica" "Teoretica" "Vocationala" levels(bac6[[5]]) <- c("Tehnologică", "Teoretică", "Vocaţională")
Funcţia table() produce un tabel de contingenţă: determină frecvenţa în cadrul setului de date, pentru fiecare combinaţie de niveluri ale factorilor indicaţi; folosim apoi funcţia prop.table() - exprimând valorile respective ca procente faţă de numărul de candidaţi din fiecare filieră:
table(bac6[c(5, 36)]) -> tst # contingenţa absolută pentru 'Filiera' şi 'status' tst <- 100*round(prop.table(tst, 1), 4) # procente faţă de numărul candidaţilor din filieră status Filiera Absent Eliminat Nepromovat Promovat Tehnologică 11.10 0.21 49.35 39.33 Teoretică 2.55 0.09 17.28 80.08 Vocaţională 3.75 0.12 27.52 68.62
Este clar că filiera "Tehnologică" are o situaţie extrem de proastă în raport cu fiecare dintre celelalte două filiere şi chiar în raport cu "suma" acestora (fapt constatat şi pentru examenul din 2015 - v. [1]): pentru "Absent", procentul este dublu faţă de suma procentelor de la celelalte două filiere; procentele de "Eliminat" şi "Nepromovat" egalează sau chiar depăşesc suma procentelor corespunzătoare pentru celelalte două filiere, iar procentul de "Promovat" este cam un sfert din suma procentelor de promovaţi de la celelalte filiere. Avem o vizualizare a proporţiilor respective (care devin arii de dreptunghiuri) prin funcţia mosaicplot():
require(RColorBrewer) # "Creates nice looking color palettes" - help(RColorBrewer) mosaicplot(tst, col = brewer.pal(4, "Accent"), las = 2, cex.axis = 0.8, main = "")
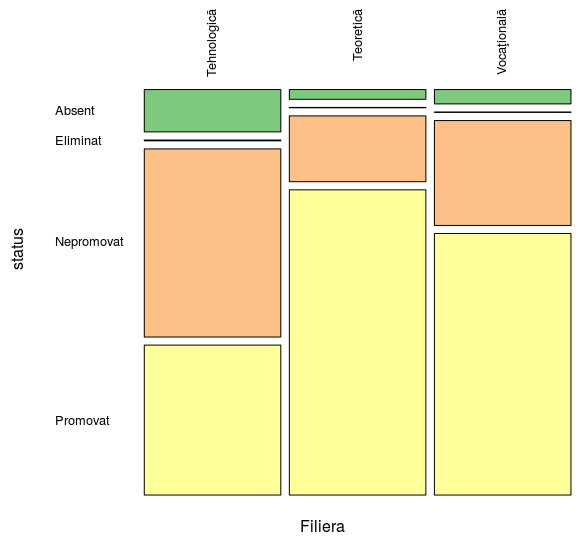
Confruntând cu situaţia din 2015 - v. [1] §9.1 - putem observa că la filiera "Teoretică" avem cam acelaşi procent de promovaţi (80.08% faţă de 80.06% în 2015) şi avem o scădere de 1% la cea "Vocaţională" şi o scădere de aproape 3% la filiera "Tehnologică".
Mai sus (şi de atâtea ori, în [1]) am sumarizat datele respective folosind table(); pentru o sumarizare "completă" (superioară din orice punct de vedere) putem folosi pachetul gmodels:
require(gmodels) CrossTable(bac6[[5]], bac6[[36]], prop.t=TRUE, prop.r=TRUE, prop.c=TRUE, prop.chisq=FALSE, dnn = c("FILIERA", "STATUS"), digits = 4)
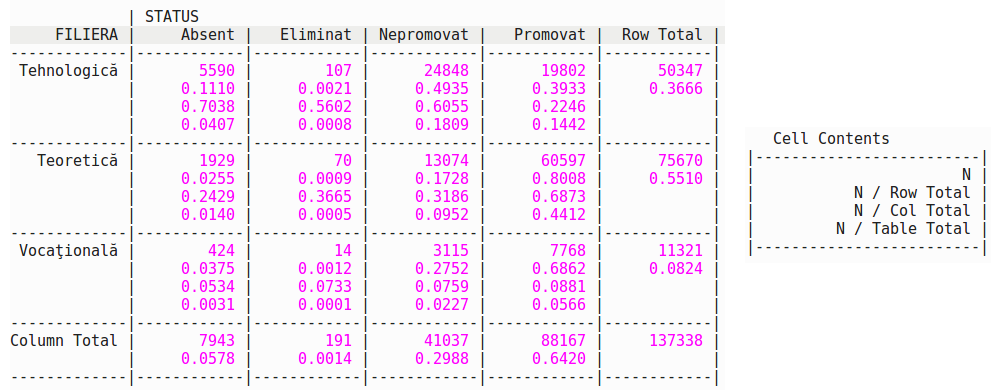
În tabelul returnat (transpus în imaginea de mai sus) avem şi frecvenţele absolute şi proporţiile lor faţă de suma pe linie, pe coloană şi respectiv faţă de numărul tuturor candidaţilor. Pe linia "Column Total" vedem că proporţiile de absenţi, nepromovaţi şi respectiv promovaţi sunt foarte apropiate de cele din 2015 (5.78%, 29.88% şi 64.20% versus 5.46%, 30.10% şi 64.12% în 2015 - v. [1]); proporţia de eliminaţi s-a redus la jumătate - 0.14% acum, faţă de 0.32% în 2015.
3. Diferenţieri privitoare la sex şi mediu
Ne ocupăm acum de reprezentarea sexelor şi a categoriilor domiciliare pe nivelurile din 'status'. Desigur, ne-ar conveni să avem un grafic pe care să putem sesiza diferenţele şi numai dacă acestea "sar în ochi" - să şi calculăm efectiv proporţiile; dar trebuie să fie clar că obţinerea graficului necesită o sumarizare prealabilă, indiferent ce pachet sau sistem grafic ai folosi (cel de bază - de unde alesesem mai sus funcţia "mosaicplot()" - sau lattice, sau ggplot2):
require(lattice) table(bac6[c('status', 'Mediu', 'Sex')]) -> TST TST <- 100*round(prop.table(TST, 2), 4) barchart(TST, # contingenţa factorilor aspect = 1, # lăţime/înălţime stack = FALSE, # cu bare alăturate xlab = "Procente", auto.key = TRUE # cu legendă )
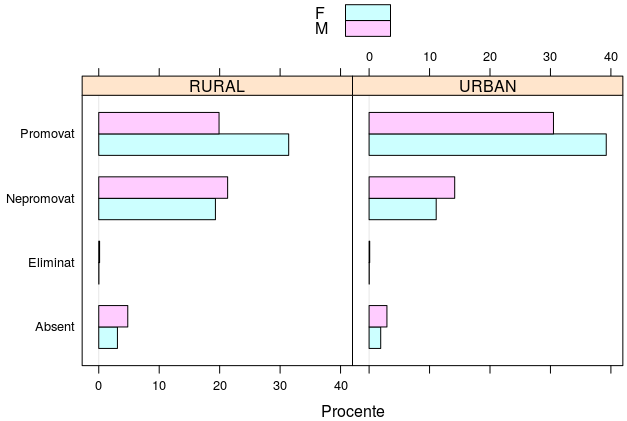
Al doilea parametru din prop.table() specifică "marginea" faţă de care se calculează proporţiile (1 pentru raportare la suma de pe linii şi 2 ca aici, pentru proporţii faţă de totalul pe coloane). Graficul evidenţiază diferenţe semnificative, în favoarea mediului "URBAN" şi a sexului "F" - la care procentul de "Promovat" este clar mai mare, iar cel de "Nepromovat" şi respectiv "Absent" este clar mai mic, faţă de "RURAL" şi "M"; de altfel, tot aşa stăteau lucrurile şi în 2015 - v. [1].
Prin funcţia ftable(), afişăm procentele din 'TST' într-un format convenabil:
ftable(TST) Sex F M status Mediu Absent RURAL 3.09 4.80 # suma 7.89% dă 'Absent' pentru 'RURAL' URBAN 1.92 2.95 Eliminat RURAL 0.03 0.14 URBAN 0.03 0.10 Nepromovat RURAL 19.30 21.32 URBAN 11.10 14.16 Promovat RURAL 31.42 19.90 URBAN 39.23 30.50
Trebuie multă grijă pentru a opera cu aceste procente. Cele două valori de pe o aceeaşi linie sunt procente ale categoriei de 'status' corespunzătoare liniei, faţă de categoria de 'Mediu' indicată pe linia respectivă; astfel pentru prima linie, 3.09 + 4.80 = 7.89% reprezintă procentul de absenţi dintre candidaţii din mediul rural, iar pentru a doua linie 1.92 + 2.95 = 4.87% ne dă procentul absenţilor din rândul candidaţilor din mediul urban - dar ar fi o greşeală monumentală să zicem că "suma" acestora 7.89 + 4.87 = 12.76% ar reprezenta procentul absenţilor din rândul tuturor candidaţilor! (pentru a obţine corect acest ultim procent, trebuie să ponderăm termenii sumei prin proporţia de "RURAL" şi respectiv de "URBAN" în masa tuturor candidaţilor).
4. Cât explică absenteismul, respingerea
Putem şi evita calculul "riscant" tocmai menţionat mai sus, de exemplu prin table():
table(bac6[[36]]) / nrow(bac6) -> ttst # proporţiile în masa tuturor candidaţilor round(ttst, 4)*100 Absent Eliminat Nepromovat Promovat 5.78 0.14 29.88 64.20 # în 2016 # 5.46 0.32 30.10 64.12 # rezultatele din 2015 (v. [1])
Am adăugat mai sus şi rezultatele din 2015, faţă de care nu avem diferenţe semnificative (exceptând procentul - mai degrabă nesemnificativ - de "Eliminat", care s-a înjumătăţit).
Să observăm că suma valorilor de pe linie este 100% (dar de obicei intervin mici erori de rotunjire); să numim "respins" situaţia acoperită de cele trei categorii distincte, diferite de "Promovat". În [1] §9.3 deschisesem o mică discuţie privitoare la măsura în care absenteismul explică statutul final de "respins", dar o pusesem oarecum incorect - în contextul situaţiei pe judeţe şi nu "global".
Problema revine la a vedea cât reprezintă 'Absent' din "respins", adică 5.78 din (100 - 64.20); rezultă imediat că proporţia absenţilor în rândul celor respinşi este de aproape 16.15% (sau, într-o formulare statistică tipică: absenteismul explică 16.15% din situaţia de respingere).
5. Diferenţierea judeţelor
Folosim iarăşi funcţia table() pentru a obţine tabelul de contingenţă pentru "jud" şi "status", apoi prop.table() pentru a relativiza valorile respective faţă de numărul de candidaţi din fiecare judeţ şi în final - ordonăm liniile matricei obţinute după procentul de promovabilitate:
table(bac6[c('jud', 'status')]) -> TST TST <- 100*round(prop.table(TST, 1), 4) TST <- TST[order(TST[, 4]), ]
Pentru a reda aici matricea rezultată (cu cele 42 de linii, ordonate crescător după coloana a patra), am pozat câte o jumătate a ei şi am reunit panourile respective în această imagine:
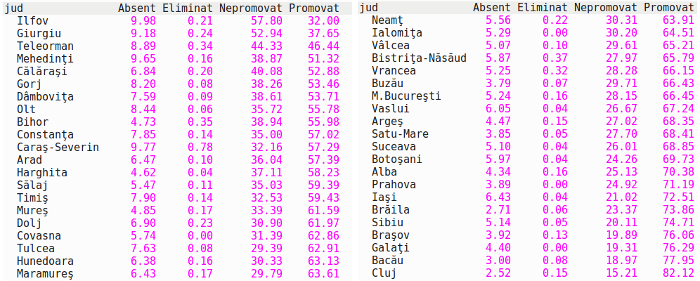
Putem obţine sumarizările standard pe fiecare coloană folosind mecanismul apply():
apply(TST, MARGIN = 2, FUN = summary) status Absent Eliminat Nepromovat Promovat Min. 2.520 0.0000 15.21 32.00 # procentul minim 1st Qu. 4.648 0.0525 26.18 57.32 # prima quartilă (25% valori - dedesubt) Median 5.650 0.1200 29.99 63.76 # a doua quartilă ("mediana" - la 50%) Mean 5.985 0.1448 31.01 62.86 # media valorilor 3rd Qu. 7.418 0.1700 35.55 68.74 # a treia quartilă (75% valori - dedesubt) Max. 9.980 0.7800 57.80 82.12 # valoarea maximă
Pentru jumătate dintre judeţe, procentul de promovabilite este în intervalul (57.32%, 68.74%) - ceva mai "strâns" faţă de 2015 (când prima şi a treia quartilă erau 56.82% şi 69.9% - v. [1] §9.3).
Putem obţine imediat o reprezentare grafică, folosind barchart(TST, ...):
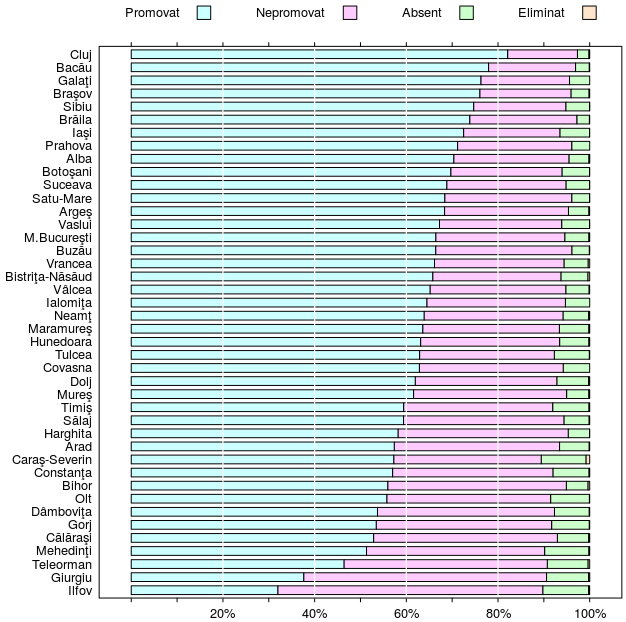
De sus în jos, judeţele figurează în ordinea descrescătoare a procentelor de promovaţi; în prealabil, am schimbat ordinea coloanelor din matricea TST încât bara grafică aferentă judeţului să marcheze întâi proporţia de promovaţi, apoi pe cea de nepromovaţi, etc. Redăm complet comanda prin care am obţinut graficul de mai sus, ilustrând maniera de precizare a parametrilor specifică pachetului "lattice":
TST[, c(4, 3, 1, 2)] -> TST # schimbă ordinea coloanelor require(lattice) barchart(TST, auto.key = list(columns = 4, # legendă orizontală cex=0.8, points=FALSE, rectangles=TRUE, size=1.5), scales = list(tck = 0.5, # gradaţii şi etichete pe axe x = list(at=seq(0, 100, by=10), labels=c("","","20%","","40%","","60%","","80%","","100%")) ), panel = function(...) { # adaugă marcaje verticale panel.barchart(...) panel.abline(v = seq(20, 90, 20), col = "white", lwd = 1.2) } )
6. Promovabilitatea pe judeţe în 2016, faţă de 2015
S-ar putea pune problema de a compara situaţia din 2016 cu aceea din 2015, pentru fiecare judeţ; ar fi destul să vizăm numai categoria 'Promovat'. Recuperăm datele "bac5" din 2015, obţinem tabelul de contingenţă pentru factorii 'jud' şi 'STATUS' (cu majuscule, în [1]), reţinem numai coloana 'Promovat' şi ordonăm vectorul rezultat după numele judeţelor:
load("../15_bac/bac5.RData") # recuperează datele din 2015 table(bac5[c('jud', 'STATUS')]) -> TST5 # proporţii de 'status', pe judeţe TST5 <- 100*round(prop.table(TST5, 1), 4) # procente tst5 <- TST5[, 4] # vectorul procentelor de 'Promovat' (2015), având ca nume judeţele tst5 <- tst5[sort(names(tst5))] # ordonează alfabetic după numele judeţelor
Vectorul rezultat mai sus, tst5 este un vector "cu nume" - fiecare valoare are asociat un nume:
head(tst5, 5) Alba Arad Argeş Bacău Bihor # numele valorii 72.26 56.79 66.10 76.47 62.44 # valoarea
Valorile pot fi accesate prin nume sau prin index (de exemplu, tst5["Bacău"], sau tst5[4]), caz în care se obţine un vector cu nume având o singură componentă; pentru a obţine una dintre valori, dar "fără nume" - se foloseşte operatorul "[[" (de exemplu, tst5[[4]] şi tst5[["Bacău"]] dau valoarea propriu-zisă, 76.47).
Să reţinem şi din matricea 'TST' (cea pentru care am făcut graficul de mai sus, pentru 2016) numai coloana 'Promovat', să ordonăm după judeţe vectorul rezultat şi apoi să îmbinăm (folosind funcţia cbind()) cei doi vectori şi să numim coloanele matricei rezultate (folosind funcţia attr()):
tst6 <- TST[, 1] # vectorul procentelor de 'Promovat' (2016), având ca nume judeţele tst6 <- tst6[sort(names(tst6))] # ordonează alfabetic după numele judeţelor PR56 <- cbind(tst5, tst6) # alătură cei doi vectori (cu aceleaşi nume de valori) attr(PR56, "dimnames")[[2]] = c("2015", "2016") # numeşte coloanele
> head(PR56, 3) # inspectăm rezultatul 2015 2016 Alba 72.26 70.38 # procent promovaţi pe 2015, respectiv pe 2016 Arad 56.79 57.39 Argeş 66.10 68.35
Obţinem acum valorile sumative tipice şi sintetizăm grafic, prin funcţia boxplot():
summary(PR56) 2015 2016 Min. :34.84 Min. :32.00 1st Qu.:56.83 1st Qu.:57.31 Median :65.83 Median :63.76 Mean :62.94 Mean :62.86 3rd Qu.:69.88 3rd Qu.:68.74 Max. :81.29 Max. :82.12 boxplot(PR56, notch=TRUE, col="#FFFFCC", border = "brown", lwd = 1.5) grid(NA, NULL)
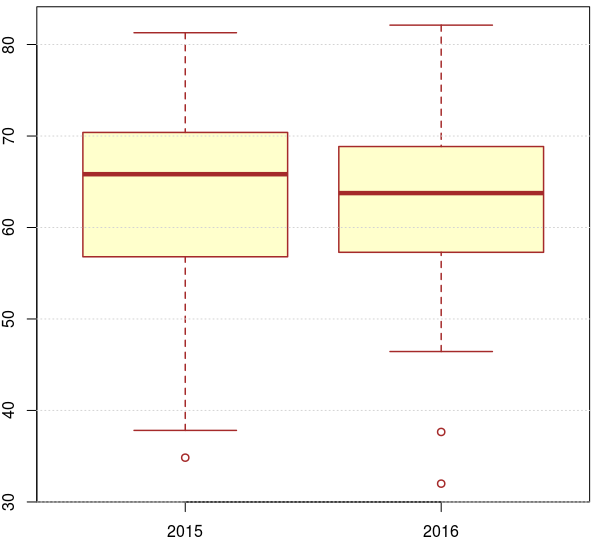
Dreptunghiurile colorate din imaginea redată mai sus reprezintă cele câte 50% valori cuprinse între prima şi a treia quartilă (Q1 şi Q3), iar liniile îngroşate reprezintă medianele (Q2), pentru 2015 şi respectiv 2016. Mediana pe 2015 împarte dreptunghiul respectiv cam în raportul 1/2 (o treime deasupra, două treimi dedesubt), în timp ce mediana pe 2016 este aproape la jumătatea înălţimii dreptunghiului corespunzător; putem zice că în 2016 valorile respective sunt distribuite mai echilibrat, decât în 2015.
Liniile orizontale scurte, legate de dreptunghi prin linii punctate, marchează limitele Q1 - 1.5×IQR şi Q3 + 1.5×IQR unde IQR = Q3 - Q1 (înălţimea dreptunghiului), iar cerculeţele marchează valori mai mici, respectiv mai mari decât aceste limite. Se vede că variaţia procentelor de 'Promovat' pe judeţe este mai mare în 2015 (în special dedesubtul medianei), decât în 2016; pe o histogramă pentru valorile respective s-ar vedea că într-adevăr, pentru 2016 avem mai puţine şi mai mici variaţii de înălţime pentru procentele respective, decât pentru 2015.
Putem evidenţia pentru fiecare judeţ, diferenţa (pozitivă sau negativă) între procentul de promovaţi pe 2016 şi cel pentru 2015, plecând de la diferenţa celor doi vectori din 'PR56':
delta <- PR56[, 2] - PR56[, 1] sort(delta, decreasing = TRUE) -> delta barchart(delta) # omitem aici, parametrii grafici
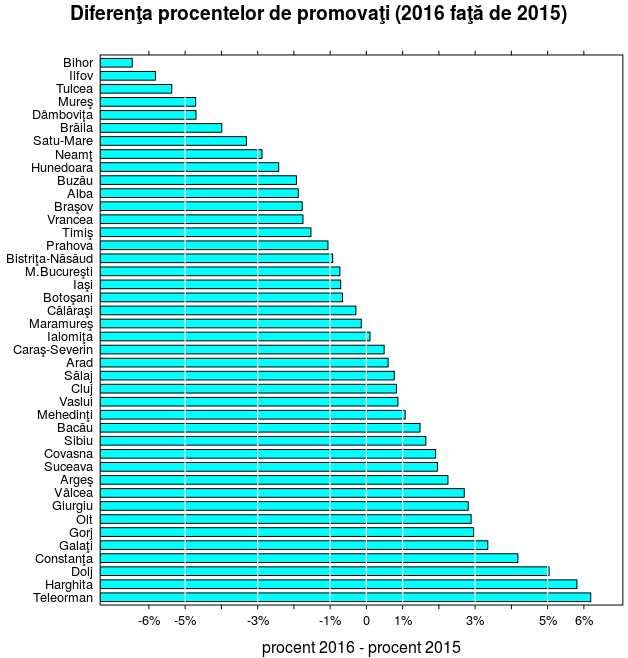
Verticala prin 0 împarte judeţele exact în două jumătăţi; de la linia pentru "Maramureş" (inclusiv) în sus avem cele 21 de judeţe pentru care diferenţa este negativă şi anume: pentru şase judeţe, procentul de promovabilitate a scăzut faţă de 2015 cu mai puţin de 1%, pentru opt judeţe (de la "Prahova" în sus) a scăzut cu 1-3%, pentru patru judeţe a scăzut cu 3-5%, iar pentru alte trei judeţe a scăzut cu mai mult de 5% (cel mai mult la "Bihor", cu peste 6%). Dedesubtul liniei "Ialomiţa" (inclusiv) avem şase judeţe care şi-au crescut procentul cu până la 1%, zece judeţe cu o creştere de 1-3%, două judeţe cu o creştere de 3-5% şi trei judeţe la care procentul a crescut cu 5-6.5% ("Teleorman" având o creştere de 6.42%).
7. Rezumarea datelor
Am văzut mai sus proporţia de absenţi şi de eliminaţi (atât "global", cât şi pe sexe, pe medii domiciliare, sau pe judeţe); mai mult de atât, nu avem ce să analizăm despre aceste categorii - încât putem elimina liniile de date corespunzătoare, urmând să ne ocupăm numai de cei care au susţinut efectiv examenul (orice proporţie vom viza mai departe, vom raporta-o numai la aceştia).
În [1] ne-am ocupat şi de nivelul competenţelor lingvistice şi digitale, precum şi de alegerea între diversele probe; aici renunţăm să mai vizăm aceste aspecte (în fond, nu avem nici un motiv să credem că - la distanţă de numai un an - am avea alte concluzii decât cele evidenţiate deja în [1]; pe de altă parte, probele de competenţe sunt cam "de umplutură" - este suficient să fii prezent, ca să nu intri în final din cauza lor, în zona de "nepromovat").
Rezultatele propriu-zise ale examenului sunt reprezentate în variabilele 'Medie' şi 'status'; mediile s-au calculat pe baza notelor obţinute la probele A..D şi după caz, luând în consideraţie şi notele acordate în urma rezolvării contestaţiilor - aşa că păstrăm şi coloanele de note şi coloanele care consemnează notele de la contestaţii, adăugând un câmp pe care să calculăm când este cazul, media "iniţială", adică aceea care ar fi rezultat dacă nu s-ar fi contestat vreuna dintre notele primite iniţial (pare interesant de comparat situaţiile mediilor dinaintea şi respectiv, de după rezolvarea contestaţiilor).
Salvăm pentru orice eventualitate datele actuale, apoi selectăm numai liniile la care 'status' nu indică 'Absent' sau 'Eliminat' (cam aceasta înseamnă "eliminare" de rânduri, în R), excluzând însă coloanele aferente competenţelor:
save(bac6, file="bac6_old.RData") bac6 <- subset(bac6, !status %in% c('Absent', 'Eliminat'), select = -c(14:26, 35)) names(bac6) # câmpurile rămase în noua structură de date, numită tot "bac6" [1] "id" "Sex" "Specializare" "Profil" "Filiera" [6] "Forma_inv" "Mediu" "sub_EA" "sub_EB" "Limba" [11] "sub_EC" "sub_ED" "Promoție" "nota_EA" "nota_EB" [16] "nota_EC" "nota_ED" "nota_cEA" "nota_cEB" "nota_cEC" [21] "nota_cED" "status" "Medie" "jud"
Am listat mai sus numele (şi indecşii) câmpurilor rămase, pentru a le putea referi mai uşor, prin index. Să înfiinţăm acum câmpul anunţat mai sus, pentru "media iniţială":
bac6$Medie1 <- apply(bac6[14:17], MARGIN = 1, FUN = mean, na.rm = TRUE) bac6[is.na(bac6$Medie), ]$Medie1 <- NA
Aici, mai întâi am aplicat pe fiecare rând de date (folosind în funcţia apply() setarea "MARGIN" = 1), funcţia mean() - pentru a calcula valoarea medie a notelor; desigur, am exclus 'nota_EB' dacă valoarea respectivă este 'NA' (însemnând că elevul respectiv nu a susţinut şi proba de "limbă maternă"). Apoi, prin a doua comandă, am "corijat" mediile tocmai determinate - înlocuindu-le cu 'NA' în situaţiile în care 'Medie' are valoarea 'NA' (fiindcă în condiţiile bacalaureatului, s-a înscris 'Medie' numai dacă toate notele pe probe sunt cel puţin 5, iar prin prima comandă calculasem media şi în aceste cazuri).
În lista numelor de câmpuri avem acum şi 'Medie1', cu indexul 25. Desigur… măcar acum, să verificăm că proporţia contestaţiilor (a notelor din câmpurile 18-21) este de luat în seamă:
apply(bac6[, 18:21], 2, function(q) sum(!is.na(q))) -> frecvenţă_contestaţii 100*round(frecvenţă_contestaţii / nrow(bac6), 4) nota_cEA nota_cEB nota_cEC nota_cED 14.21 0.36 10.34 9.25
Faţă de 2015 (v. [1] §6), proporţia de contestaţii s-a mărit pe fiecare probă cam cu câte 1-3% (de exemplu, la "proba C" este 10.3% şi era 7.8% în 2015). Putem estima (ţinând cont că unii candidaţi au contestat mai mult decât o singură probă) că proporţia contestaţiilor este una semnificativă (în jur de 14%) - deci înfiinţarea mai sus a câmpului 'Medie1' nu este lipsită de sens.
8. Distribuţia globală a mediilor
În [2] - influenţat de reminiscenţe privitoare la rezolvarea "cu multă bunăvoinţă" a contestaţiilor - exprimam bănuiala că distribuţia notelor dinaintea contestaţiilor (adică în termenii de acum, a valorilor 'Medie1') se apropie de distribuţia normală, spre deosebire de cea constatată pentru mediile finale. Putem recunoaşte acum că lucrurile nu stau deloc aşa: valorile sumative tipice s-au mărit în urma rezolvării contestaţiilor cu numai 1-3 sutimi (exceptând valoarea minimă, care a coborât la 4.28 - însemnând că unele note care iniţial erau mai mari ca 5 şi care au fost contestate, au devenit în final mai mici decât 5); iar curbele care estimează densitatea distribuţiei pentru cele două situaţii, diferă foarte puţin între ele (şi diferă destul de clar, de o distribuţie normală):
summary(bac6[c(23, 25)]) Medie Medie1 Min. : 5.00 Min. : 4.28 1st Qu.: 6.73 1st Qu.: 6.72 Median : 7.83 Median : 7.82 Mean : 7.75 Mean : 7.73 3rd Qu.: 8.80 3rd Qu.: 8.77 Max. :10.00 Max. :10.00 NA's :32612 NA's :32612 dens <- density(bac6$Medie, from = 5, to = 10, adjust = 1, na.rm = TRUE) dens1 <- density(bac6$Medie1, from = 4.25, to = 10, adjust = 1, na.rm = TRUE) plot(dens1, col = "blue", main = "Densitatea mediilor înainte şi după contestaţii") lines(dens)
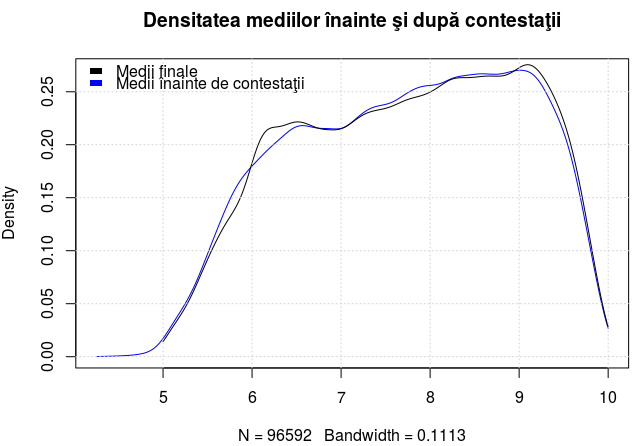
Pe intervalul [5, 6] curba marcată cu negru (corespunzătoare mediilor finale) este dedesubtul curbei marcate cu albastru (pentru mediile dinaintea contestării) - ceea ce înseamnă că proporţia de medii între 5 şi 6 era ceva mai mare înaintea rezolvării contestaţiilor, decât după aceea (când o parte a coborât sub 5, iar o parte a urcat peste 6); la fel, proporţia mediilor între 7 şi 8 era mai mare înainte, decât după contestaţii. În schimb, proporţia mediilor între 6 şi 6.5 şi la fel, între 9 şi 9.5 - s-a mărit (sensibil, pe grafic) în urma rezolvării contestaţiilor.
Curba mediilor dinaintea contestaţiilor este mai "netedă" (are variaţii de înălţime mai mici şi mai puţine), decât cea corespunzătoare mediilor finale. Ca formă generală, avem cam acelaşi tip de distribuţie ca şi în 2015 (v. [2]) şi putem bănui că la fel vor sta lucrurile în 2017, sau 2018.
Înainte de a abandona ideea considerării mediilor "iniţiale" (dovedită aici ca fiind mai degrabă irelevantă), să retrângem investigaţia redată mai sus la un judeţ oarecare. Cu levels() găsim vectorul numelor de judeţe, alegem unul la întâmplare folosind sample() şi reluăm (pentru mediile din acel judeţ) secvenţa comenzilor de plotare a densităţilor folosită mai sus:
judeţ <- levels(bac6$jud)[sample(1:42, 1)] ds <- density( bac6[bac6$jud == judeţ, ]$Medie, from = 5, to = 10, na.rm = TRUE ) ds1 <- density( bac6[bac6$jud == judeţ, ]$Medie1, from = 4.25, to = 10, na.rm = TRUE ) plot(ds1, col = "blue", ylim = c(0, 0.35), main = paste("Densitatea mediilor", judeţ)) lines(ds)
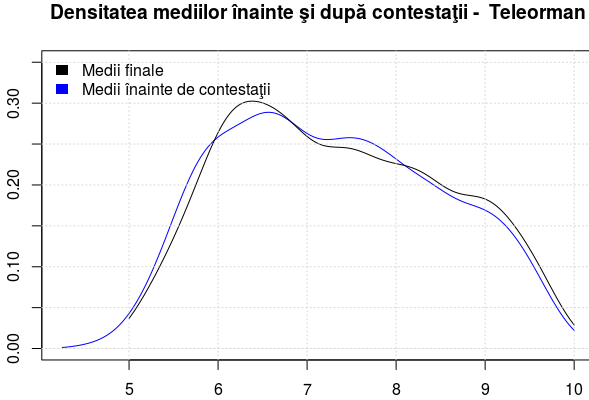
După câteva repetiţii, am obţinut cazul redat grafic mai sus, al unui judeţ cu media judeţeană mai mică (vârful densităţii s-a mutat spre stânga, între 6 şi 7); în acest caz particular, avem o diferenţă mai pronunţată între cele două curbe.
9. Distribuţiile de medii pe judeţe
Ca şi în [2], vrem să vizualizăm curbele care estimează densitatea distribuţiei notelor pe fiecare judeţ, în ordinea valorilor mediei judeţene (care să fie şi aceasta redată pe grafic, alături de numele judeţului); dar vom proceda mai simplu ca în [2], pentru a reordona nivelurile factorului 'jud' după mediile respective şi pentru a include în acelaşi timp, aceste medii.
Mai întâi creem separat (din raţiuni didactice, dar şi pentru prudenţă) un 'factor' ordonat după mediile judeţene, folosind funcţia reorder():
rejud <- reorder(bac6$jud, bac6$Medie, FUN = mean, order = TRUE, na.rm = TRUE) str(rejud) # inspectăm structura de date rezultată Ord.factor w/ 42 levels "Ilfov"<"Giurgiu"<..: 7 21 24 3 7 12 24 41 24 18 ... - attr(*, "scores")= num [1:42(1d)] 7.87 7.53 7.72 7.93 7.65 ... ..- attr(*, "dimnames")=List of 1 .. ..$ : chr [1:42] "Alba" "Arad" "Argeş" "Bacău" ...
Deja avem şi vectorul mediilor judeţene, în atributul "scores" (şi nu va trebui să le recalculăm prin aggregate() - cum ni s-a părut necesar în [2]); nivelurile factorului rezultat sunt ordonate în ordinea crescătoare a mediilor judeţene ("Ilfov"<"Giurgiu"<...), dar valorile din 'scores' respectă ordinea iniţială, păstrată în atributul 'dimnames'. Ordonăm crescător vectorul din 'scores' (folosind funcţia sort()), instituim ca etichete pentru afişări (prin parametrul 'labels') alipirile (prin funcţia paste()) de nume de judeţe şi respectiv, medii judeţene şi redefinim astfel factorul 'jud' din "bac6":
bac6$jud <- factor(rejud, levels = levels(rejud), labels = paste(levels(rejud), round(sort(attr(rejud,"scores")), 2))) bac6 <- bac6[order(bac6$jud), ] # înregistrează noii indecşi ai nivelurilor 'jud' str(bac6$jud) # verificăm rezultatul Ord.factor w/ 42 levels "Ilfov 7"<"Giurgiu 7.18"<..: 1 1 1 1 1 1 1 1 1 1 ...
Vedem în final că mediile apar alături de numele judeţelor şi acum, liniile de date din "bac6" sunt redate în ordinea dată de mediile judeţene (primele "1 1 ..." corespund la "Ilfov 7", etc.).
Faţă de comanda folosită în [2] pentru vizualizarea grafică a densităţilor, nu avem de modificat decât parametrul 'data' (şi doar titlul):
require(lattice) densityplot( ~ Medie | jud, # densitatea notelor, pe fiecare judeţ în parte data = bac6, # subset = as.numeric(jud) %in% c(8, 10, 13, 26), # pentru un grup de judeţe from = 5, to = 10, n = 128, # pentru calculul densităţii type = "g", aspect = 0.5, # grid, înălţime/lăţime=0.5 par.strip.text = list(cex=0.8), # reduce mărimea de scriere a etichetelor layout = c(7, 6), # 6 linii a câte 7 panouri (42 judeţe) as.table = TRUE, # de la stânga la dreapta, de sus în jos main = list(label = "Distribuţia mediilor în judeţe (BAC 2016)", # titlu font=3, col="cornsilk4") ) -> dst_list # listă cu toate datele şi setările necesare trasării graficului plot(dst_list)
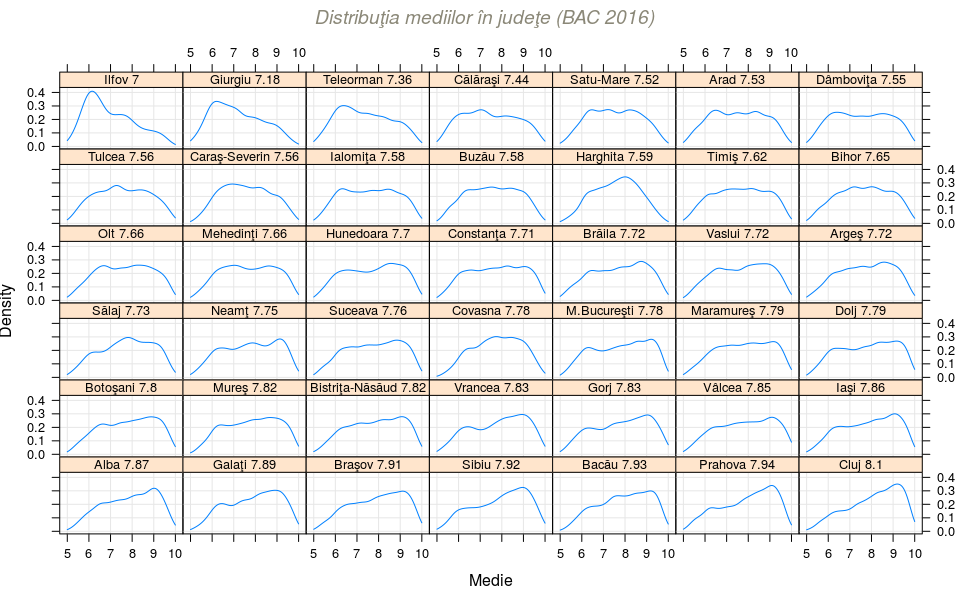
Putem zice - ca şi în [1], pentru 2015 - că distribuţiile redate prin curbele de mai sus nu prea seamănă cu cele normale (cum ne aşteptăm, de regulă); avem câte un vârf cu înălţimea cam de 25%-30% (depăşind 30% numai în vreo patru cazuri), care pe măsură ce media judeţeană creşte (uitându-ne pe cele 42 de grafice de la stânga la dreapta şi de sus în jos), se mută dinspre zona mediilor 6-7 (începând ca şi în 2015, cu "Ilfov 7") spre zona mediilor 8 (terminând la "Cluj 8.1").
Această trecere a vârfului din poziţia stânga-sus (proporţie majoritară de medii mici) spre poziţia dreapta-sus (proporţie majoritară de medii mari) se poate sesiza mai uşor urmărind cele câte şase curbe de pe fiecare coloană (reprezentând distribuţiile a câte şase judeţe distanţate din 7 în 7, pe scara mediilor judeţene).
10. Alte distribuţii de medii
Am văzut în §2 că proporţia de promovaţi este mult mai mare la filiera "Teoretică" decât la cea "Tehnologică"; ar fi interesant de comparat şi distribuţiile mediilor, pentru aceste două filiere:
ds1 <- density( bac6[bac6$Filiera == "Teoretică", ]$Medie, from = 5, to = 10, na.rm = TRUE ) ds2 <- density( bac6[bac6$Filiera == "Tehnologică", ]$Medie, from = 5, to = 10, na.rm = TRUE ) plot(ds1, col="blue", main = "Densitatea mediilor - 'Teoretică' v. 'Tehnologică'") lines(ds2, col = "red"); grid() legend('bottom', c('filiera Teoretică', 'filiera Tehnologică'), fill = c("blue", "red"), bty = 'n', border = NA)
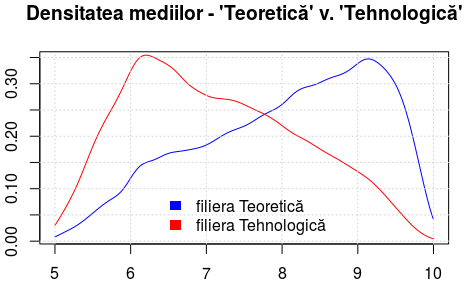
Proporţia mediilor mici - sub 7.75, apreciind după graficul redat mai sus - este cam de două ori mai mare la filiera "Tehnologică", decât la "Teoretică"; simetric - proporţia mediilor "mari" (de la 7.75 la 10) este chiar mai mare de două ori, la "Teoretică" decât la "Tehnologică" (proporţiile de care vorbim fiind "măsurate" prin ariile subântinse de porţiunile respective - până la 7.75 (intersecţia curbelor) şi respectiv, dincolo de 7.75 - ale celor două curbe de densitate).
Am zice până la urmă, că este greu de justificat o legătură între filiera "Tehnologică" pe de o parte şi "bacalaureat" (cu probele clasice), pe de altă parte.
Adaptând secvenţa de comenzi redată mai sus mai sus, putem compara distribuţiile de medii pentru diverse alte categorii. Procedând astfel - ni s-a părut că pentru candidaţii proveniţi din seriile anterioare ultimei promoţii de absolvenţi, curba de densitate a mediilor se apropie de cea normală (curba lui Gauss) - încât rescriem secvenţa respectivă, pentru a plota şi curbele normale.
Selectăm numai coloana 'Medie' (şi anume, valorile diferite de 'NA') pentru promoţia curentă şi respectiv pentru cele anterioare, determinăm valorile medii şi dispersiile corespunzătoare (necesare funcţiei dnorm() pentru constituirea valorilor corespunzătoare unei distribuţii normale, cu media şi dispersia respectivă) şi plotăm curbele (folosind parametri grafici pe care i-am mai prezentat şi folosit anterior, inclusiv în [1] şi [2]):
serie1 <- bac6[bac6$Promoție == "2015-2016" & !is.na(bac6$Medie), ]$Medie serie2 <- bac6[bac6$Promoție == "OTHER" & !is.na(bac6$Medie), ]$Medie m2 <- mean(serie2); m1 <- mean(serie1) # m2=6.08, m1=7.93 (valorile medii) sd2 <- sd(serie2); sd1 <- sd(serie1) # sd2=0.54, sd1=1.14 (dispersiile) ds1 <- density(serie1, from = 5, to = 10) ds2 <- density(serie2, from = 5, to = 9.55) opar <- par(mar = c(2,2,2,0) + 0.1, cex.axis = 0.75) plot(ds2, col="red", cex.main=1, main="Densitatea mediilor ultimei promoţii şi a celor mai vechi") lines(ds2$x, dnorm(ds2$x, mean = m2, sd = sd2), lwd=1.5, col="magenta", lty=3) lines(ds1, col="blue") lines(ds1$x, dnorm(ds1$x, mean = m1, sd = sd1), lwd=1.5, col="darkcyan", lty=3) grid() legend('topright', c('2015-2016 (87319 candidaţi)', 'alte promoţii (9273 candidaţi)', 'curba normală, 2015-2016', 'curba normală - alte promoţii'), fill = c("blue", "red", "darkcyan", "magenta"), bty='n', border=NA, cex=0.8) par(opar)
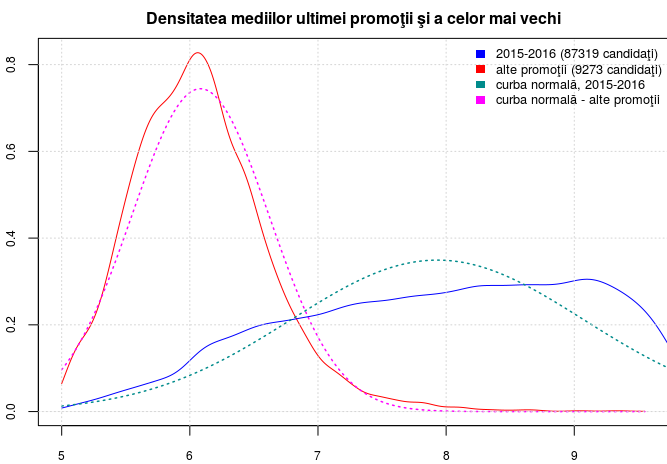
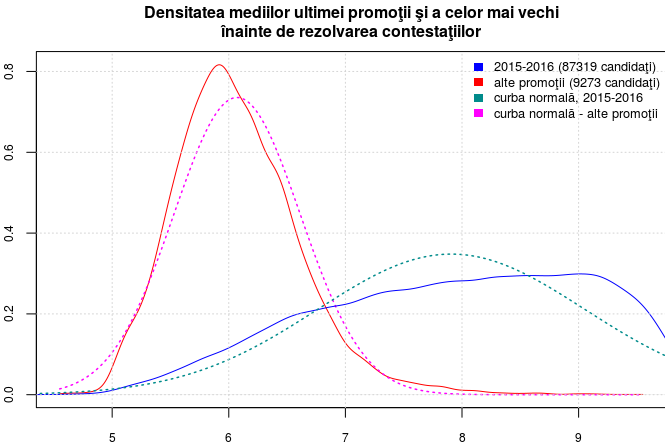
Profitând de faptul că am determinat anterior şi mediile dinaintea rezolvării contestaţiilor, am repetat secvenţa redată mai sus înlocuind 'Medie' cu 'Medie1' - obţinând graficul din partea dreaptă (desigur, am avut în vedere faptul că prin recorectare, unele medii au coborât sub 4 şi am schimbat valoarea parametrului 'from' din apelurile density(); în rest, am schimbat doar titlul graficului).
Diferenţa dintre densitatea mediilor dinainte (graficul din dreapta) şi de după contestaţii (graficul din stânga) este mult mai pronunţată în cazul "alte promoţii" (pe curbele colorate cu roşu), decât în cazul "2015-2016" (pe curbele colorate cu albastru); în ambele cazuri (dar ceva mai pronunţat pe roşu, adică pentru "alte promoţii") deosebirea cea mai mare apare în imediata vecinătate a mediei 6. S-ar zice după graficele redate, că reprezentaţii seriilor mai vechi şi-au gestionat mai eficient decât cei din ultima promoţie, dreptul de a contesta (reuşind să urce într-o proporţie mai mare, de undeva din spatele mediei 6 undeva puţin peste aceasta).
11. Simularea normalităţii
Este firesc să comparăm distribuţia notelor cu o distribuţie teoretică - de obicei, cu distribuţia normală N(μ, σ), având ca parametri media şi dispersia valorilor date.
Interesaţi fiind de organizarea şi desfăşurarea examenului "naţional" - poate să convină mai degrabă asemenea artificii, decât să comparăm rezultatele examenului chiar cu situaţia reală reflectată de cataloagele şcolare; dacă s-ar face chiar această comparaţie - cel mai probabil s-ar descoperi că în privinţa rezultatelor, examenul final nu prea are sens, întrucât rezultatele acestuia, mai bune sau mai rele de la un candidat la altul, corespund în foarte mare măsură situaţiei şcolare mai bune sau mai rele a candidatului (încât însăşi situaţia şcolară la obiectele de bază, cumulată în cei patru ani de liceu în cataloage, ar putea foarte bine să certifice direct un 'status' de "bacalaureat").
Pentru a compara două distribuţii X şi Y (având să zicem, aceeaşi lungime n) putem folosi metoda grafică Q-Q plot, bazată pe următoarea idee: determinăm valorile xk ∈ X şi yk ∈ Y la care avem aceiaşi frecvenţă cumulată crescător k/n (k=1..n) - adică pentru care avem P(X < xk) ≈ P(Y < yk) ≈ k/n; dacă xk ≈ yk, k=1..n - sau mai general, dacă punctele (xk, yk) apar aproape de o aceeaşi dreaptă - atunci se poate considera că X şi Y provin dintr-o aceeaşi distribuţie.
Exemplificăm construcţia unui punct al graficului "Q-Q plot": determinăm frecvenţa relativă cumulată crescător a valorii 6 pentru mediile finale, iar pentru mediile "iniţiale" - după câteva încercări - găsim aproximativ aceeaşi frecvenţă pentru valoarea 5.93:
medii <- bac6[!is.na(bac6$Medie), ]$Medie # mediile finale medii1 <- bac6[!is.na(bac6$Medie1), ]$Medie1 # mediile dinaintea contestaţiilor length(medii[medii < 6]) / length(medii) # frecvenţa cumulată crecător a valorii 6 [1] 0.08722254 # P(medii < 6) ≈ 0.87 length(medii1[medii1 < 5.93]) / length(medii1) [1] 0.08706725 # P(medii1 < 5.93) ≈ 0.87
Graficul "Q-Q plot" va conţine punctul (6, 5.93), situat puţin dedesubtul dreptei y[medii1] = x[medii], cum se poate observa pe primul grafic redat mai jos (mărind în jurul punctului (6, 6)).
Funcţia quantile() returnează un vector "cu nume":
quantile(medii, seq(0, 1, 0.1)) 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% 5.00 6.05 6.51 6.96 7.41 7.83 8.23 8.61 9.00 9.36 10.00
Numele reprezintă procentual "frecvenţele relative" cumulate crescător din secvenţa primită ca parametru, iar valorile sunt cele pentru care se ating "câtimile" respective ('quantillus' s-ar traduce prin "câtime"); în exemplul redat mai sus, vedem că 10% dintre mediile finale sunt mai mici ca 6.05, apoi 50% dintre ele sunt mai mici ca 7.83, ş.a.m.d.
Prin secvenţa următoare, determinăm "cuantilele" corespunzătoare fiecărei unităţi procentuale în vectorii de medii respectivi şi plotăm punctele rezultate - obţinând primul dintre cele două grafice alăturate redate mai jos:
prob <- seq(0, 1, 0.01) # o gamă de probabilităţi (din sutime în sutime) qm <- quantile(medii, prob) # valorile xk pentru care P(X < xk) = prob qm1 <- quantile(medii1, prob) old_par <- par(cex=0.8, pty="s", pch=20) # reconfigurează unii parametri grafici globali plot(qm, qm1, col="firebrick2", cex=0.5, xlab="Medii finale", ylab="Medii înainte de contestaţii", main="Q-Q plot: medii finale vs. medii iniţiale") abline(0, 1, col="blue", lwd=0.75) # diagonala (5, 5)--(10, 10) grid(); par(old_par) # reconstituie parametrii grafici iniţiali
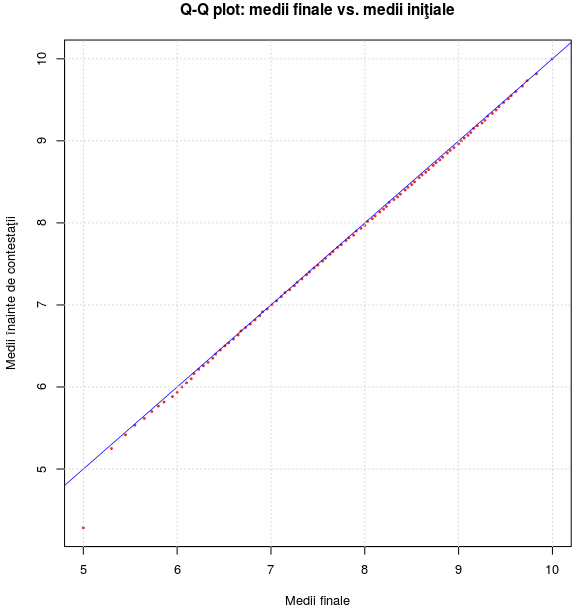
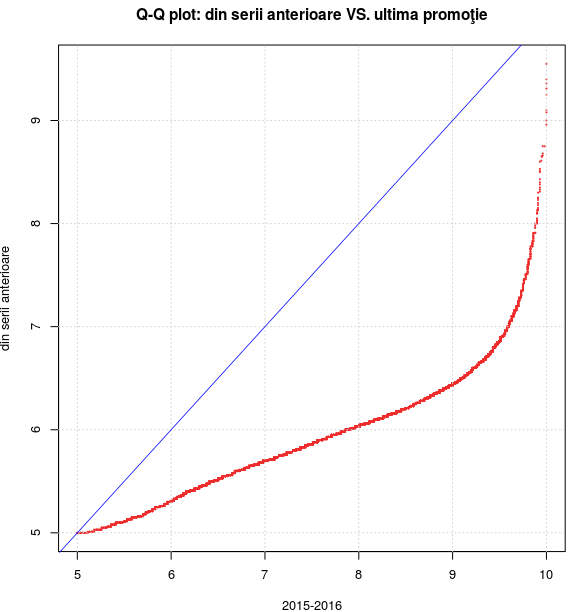
Graficul obţinut (primul din stânga) denotă că mediile finale şi respectiv, mediile "iniţiale" pot fi considerate ca având aceeaşi distribuţie ("câtimile" corespunzătoare fiind aproximativ egale).
Graficul din partea dreaptă a fost obţinut invocând direct funcţia qqplot(serie1, serie2, ...) care înglobează aproximativ secvenţa de comenzi redată mai sus şi în plus, are în vedere dimensiunile vectorilor (dacă acestea diferă - cum este cazul vectorilor serie1 şi serie2 - atunci se aplică un anumit procedeu de interpolare, pentru determinarea "cuantilelor" reprezentative). Graficul arată că distribuţia mediilor candidaţilor din ultima promoţie şi cea a mediilor candidaţilor proveniţi din promoţiile anterioare nu pot fi considerate ca provenind dintr-o aceeaşi distribuţie de valori; de exemplu, curba trece aproximativ prin punctul de coordonate (8, 6) - ceea ce înseamnă că proporţia celor din seria 2015-2016 cu media mai mică decât 8 este cam aceeaşi cu aceea a celor din promoţiile anterioare cu media mai mică decât 6 (şi nu tot 8, ca în cazul când ar fi originat dintr-o aceeaşi distribuţie); şi cam aceeaşi situaţie avem, pe tot parcursul curbei "Q-Q plot" respective.
Acum, să comparăm distribuţia mediilor finale cu distribuţia normală: sunt "câtimile" acestora cam aceleaşi cu cele dintr-o distribuţie normală de valori a căror medie şi dispersie sunt egale respectiv cu media şi dispersia valorilor din 'medii'?
De exemplu, mai sus calculasem P(medii < 6) ≈ 0.872 (adică 8.72% dintre medii sunt sub 6); pentru "câtimea" 0.872, obţinem cam aceeaşi valoare 6 şi pentru distribuţia normală? Răspunsul poate fi obţinut prin funcţia qnorm():
qnorm(0.0872, mean = mean(medii), sd = sd(medii)) [1] 6.088624 # cu cel mult 9 sutimi mai mare ca valoarea din distribuţia reală, 6
În acest caz, diferenţa (sub 9 sutimi) este nesemnificativă; în alte cazuri, avem o diferenţă ceva mai mare - de exemplu, pentru P(medii < 9) avem o diferenţă de aproape 22 de sutimi:
length(medii[medii < 9]) / length(medii) [1] 0.7997453 # 7.99% medii sub 9 qnorm(0.799, mean = mean(medii), sd = sd(medii)) [1] 8.781876 # cu 22 sutimi mai jos de 9 (în distribuţia normală)
Funcţia qqnorm() modelează un calcul de natura celui exemplificat mai sus şi plotează punctele care împerechează valorile crescătoare din vectorul primit ca parametru şi respectiv (în acelaşi număr şi în aceeaşi ordine ca şi aceste valori), cuantilele distribuţiei normale standard (de medie 0 şi dispersie 1). Putem improviza construcţia funcţiei qqnorm() prin următorul experiment:
Y <- sample(medii, 10) # selectăm aleatoriu 10 valori din vectorul 'medii' index <- order(Y) # indicii valorilor de aşezat în ordinea crescătoare a acestora data.frame(Y, index) # inspectăm valorile şi indecşii Y index#-ul valorilor de aşezat în ordinea crescătoare 1 7.43 9 # cea mai mică este valoarea a 9-a, 5.68 2 6.15 2 # a doua cea mai mică este chiar valoarea a 2-a, 6.15 3 6.46 3 # 6.46 este a treia în ordine crescătoare 4 8.83 6 # a patra: valoarea a 6-a, 6.46 5 8.00 8 # a cincea: valoarea a 8-a, 7.03 6 6.46 7 # a şasea: valoarea a 7-a, 7.05 7 7.05 1 # a şaptea: valoarea de rang iniţial 1, 7.43 8 7.03 10 # a opta: valoarea de rang iniţial 10, 7.95 9 5.68 5 # a noua: valoarea de rang iniţial 5, 8 10 7.95 4 # a zecea: valoarea de rang iniţial 4, 8.83 prob <- ppoints(10, a = 0.5) # 10 "câtimi" de unitate, (k - 0.5)/10, k=1..10 prob # (1-0.5)/10, (2-0.5)/10, (3-0.5)/10 etc. [1] 0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95 X <- qnorm(prob) # valorile x la care P(X <= x) == prob, X ∈ N(μ=0, σ=1) X <- X[order(index)] # ordonează X după indicii valorilor crescătoare din Y data.frame(X, index=order(X)) X index#-ul valorilor crescătoare (acelaşi ca la Y) 1 0.3853205 9 2 -1.0364334 2 3 -0.6744898 3 4 1.6448536 6 5 1.0364334 8 6 -0.3853205 7 7 0.1256613 1 8 -0.1256613 10 9 -1.6448536 5 10 0.6744898 4 plot(X, Y)
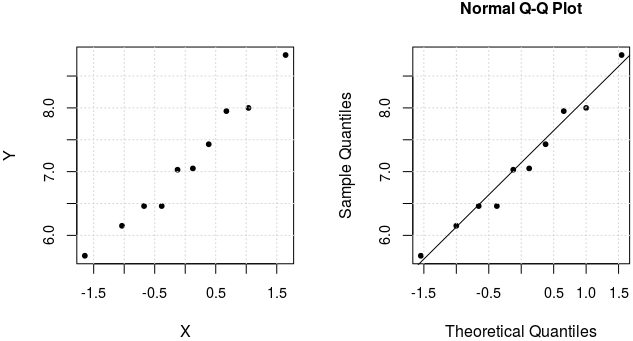
Ultima comandă a plotat punctele de indecşi (9, 9) adică (-1.6448536, 5.68), respectiv de indici (2, 2) adică (-1.0364334, 6.15), ş.a.m.d., al zecelea punct fiind cel de indecşi (4, 4) adică punctul (1.6448536, 8.83) - cum se poate intui mărind primul grafic din imaginea redată mai sus. Graficul din dreapta atestă faptul că secvenţa de comenzi improvizată mai sus produce într-adevăr, graficul "Q-Q plot" realizat prin următoarea invocare directă a comenzii qqplot():
qqnorm(Y); qqline(Y)
qqline() trasează dreapta care uneşte punctul care corespunde primei cuartile Q1 a valorilor Y, cu cel asociat cu a treia cuartilă Q3; cele zece puncte fiind apropiate acestei dreapte, putem aprecia cu suficientă încredere, că valorile din Y au o distribuţie apropiată de cea normală (dar aceasta este o întâmplare; am repetat de câteva ori execuţia secvenţei de mai sus, obţinând puncte mai degrabă "nealiniate").
Prin secvenţa următoare obţinem cele patru grafice redate dedesubt:
n = length(medii); miu = mean(medii); sigma = sd(medii) # lungimea, media, dispersia old_par <- par(mfrow = c(1, 4), # patru panouri grafice alăturate pty = "s", pch = 20, # panouri pătratice; simbolul folosit pentru puncte cex.main = 1.2, cex.axis = 0.9) # scalează titluri şi etichetări # car::qqPlot() are o serie de facilităţi faţă de qqnorm() require(car) qqPlot(medii, line = "robust", # dreapta "cea mai apropiată" de punctele respective col="orange", cex = 0.2, # culoare, factor de scalare pentru puncte lwd = 1, # lăţimea dreptei main = expression(paste("(1) Medii 2016 vs. N(", mu, ", ", sigma, ")")))
# generăm aleatoriu valori distribuite normal cu aceiaşi parametri ca ai vectorului 'medii' simul_medii <- rnorm(n, mean = miu, sd = sigma) qqnorm(simul_medii, col="orange", cex = 0.6, main = expression(paste("(2) simulare N(", mu, ", ", sigma, ")"))) qqline(simul_medii); grid()
# valori aleatorii din intervalul [5, 10] (păstrând parametrii din 'medii') simul_medii <- trun_rnorm(n, mean = miu, sd = sigma, low = 5, high = 10) qqnorm(simul_medii, col = "orange", cex = 0.6, main = expression(paste("(3) simulare N(", mu, ", ", sigma, ")", " cu trunchiere [5, 10]"))) qqline(simul_medii); grid()
# generăm toate valorile cu câte două zecimale, aflate între 5 şi 10 # şi selectăm aleatoriu n dintre acestea, comparând cu distribuţia normală # (dar media şi dispersia selecţiei diferă de ale vectorului 'medii') sample(seq(5, 10, 0.01), size = n, replace = TRUE) -> simul_medii qqnorm(simul_medii, col = "orange", cex = 0.6, cex.main = 1, main = "(4) 'sample()' valori [5, 10] cu câte 2 zecimale") qqline(simul_medii); grid() difer = round(c(mean(simul_medii) - miu, sd(simul_medii) - sigma), 2) legend("topleft", c(paste("difer. Medie = ", difer[1]), paste("difer. Dispersie = ", difer[2])), bty = 'n', border = NA, cex = 0.8) par(old_par) # reconstituie parametrii grafici iniţiali
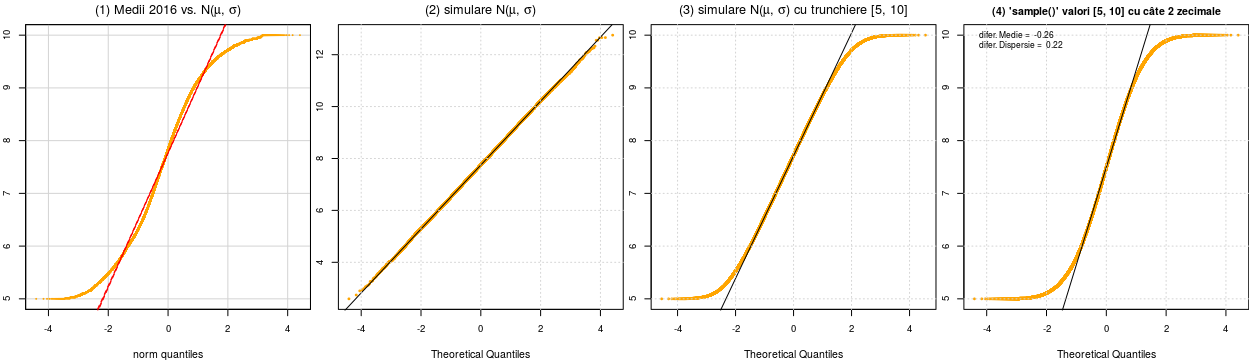
Mai întâi, am comparat 'medii' cu distribuţia normală - folosind funcţia qqPlot() din pachetul car (aceasta are unele avantaje faţă de qqnorm(); de exemplu, trasează "dreapta de regresie" a punctelor - dreapta faţă de care suma pătratelor abaterilor verticale ale punctelor este minimă - în loc de aceea care uneşte prima şi a treia cuartilă); graficul rezultat (1) arată că 'medii' nu ţine totuşi, de o distribuţie normală ("cozile" spre stânga şi spre dreapta ies din tiparul normal).
Apoi, am generat aleatoriu (prin funcţia rnorm()) valori distribuite normal cu aceiaşi parametri ca ai vectorului 'medii', obţinând (prin qqnorm() şi qqline()) graficul (2); dar astfel, obţinem şi valori mai mici decât 5, sau mai mari ca 10. Alinierea punctelor de-a lungul diagonalei pătratului confirmă normalitatea distribuţiei astfel generate.
Am încercat apoi, să obţinem numai valori din intervalul [5, 10] - folosind această funcţie:
trun_rnorm <- function(n, mean, sd, low, high) { x <- rnorm(2*n, mean, sd) x[x >= low & x <= high] }
Aceasta ar suplini faptul că rnorm() nu prevede parametri de limitare a valorilor generate; dar şansele de a păstra caracterul aleatoriu - prin reţinerea numai a valorilor limitate prin parametrii 'low' şi 'high', dintre cele (în număr dublu) generate prin rnorm() - sunt mici (iar numărul de valori furnizate în final nu mai este sub control). Graficul (3) obţinut astfel arată că de fapt, valorile astfel furnizate nu corespund unei distribuţii normale (cozile fiind iarăşi, în afara tiparului normal).
În sfârşit, ne dăm seama şi de acest fapt: valorile din 'medii' sunt numere cu un format specific - au cel mult două zecimale (lucru de care nu am ţinut cont în cursul simulărilor descrise mai sus). Am considerat secvenţa celor 501 valori posibile de forma "n.nn" (de la 5, 5.01, 5.02, ..., 5.99, 6, 6.01, ... până la 9.99, 10) şi am ales aleatoriu, cu repetiţie (folosind funcţia sample()) un număr de astfel de valori egal cu lungimea vectorului 'medii'; desigur, media şi dispersia valorilor astfel obţinute diferă (dar nu mult) de valorile respective pentru 'medii'. Graficul (4) rezultat în final, arată că nici aşa nu avem o distribuţie normală.
Odată de mult - tânăr profesor fiind - un inspector şcolar mi-a arătat histograma notelor pentru extemporalul pe care-l dăduse clasei mele şi mi-a explicat că ea nu corespunde "clopotului lui Gauss" - semn că subiectul respectiv a fost prea greu pentru elevi (deşi el era conform programei şcolare). Cu siguranţă că avea dreptate şi de atunci păstrez ideea că notele sau mediile şcolare ar trebui să aibă o distribuţie apropiată de cea normală; dar experimentele şi simulările redate mai sus dau această lecţie finală: normalitatea este o iluzie şi este chiar greu de simulat.
vezi Cărţile mele (de programare)