Se mai întâmplă să mă trezesc cu câte o idee clară în minte, legată de ceea ce mă preocupă…

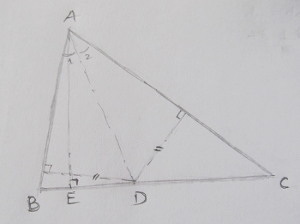Fie D piciorul bisectoarei din vârful A al triunghiului ABC şi E piciorul înălţimii din A. Triunghiurile ADB şi ADC au o aceeaşi înălţime din A; pe de altă parte, înălţimile din D ale lor sunt egale, ca fiind distanţele punctului D la laturile AB şi respectiv AC ale unghiului bisectat de AD. Raportul ariilor triunghiurilor ADB şi ADC este egal pe de o parte cu DB/DC (considerând înălţimea comună AE şi bazele DB, respectiv DC), iar pe de altă parte cu AB/AC (având înălţimi egale din D, faţă de bazele AB şi respectiv AC). Rezultă că DB/DC = AB/AC - adică: bisectoarea împarte latura pe care cade într-un raport egal cu raportul laturilor unghiului.

Am destulă experienţă încât să nu cad în păcatul de a crede că m-am trezit cu o demonstraţie nouă sau originală, pentru clasica "teorema bisectoarei". În treacăt fie spus, demonstraţia dată de Euclid (reprodusă în toate manualele de geometrie elementară) - este elegantă şi profundă: construim BB' (B'∈AC) paralelă cu bisectoarea AD (iată "profunzimea": este implicată direct, axioma paralelelor) şi explicităm asemănarea triunghiurilor constituite astfel (observând că triunghiul ABB' este isoscel).

Dar ce preocupări obsesive şi ce dileme, să-mi fi determinat întruchiparea de mai sus?!

În ultimii ani n-am fost deloc în postura de a alege - "plătind" în fond pentru evitarea continuă a eforturilor şi precauţiilor necesare obţinerii şi conservării unui post sau statut cât mai potrivit pregătirii mele. Iar în acest an şcolar am PATRU clase a IX-a, cu profilul "turism", "comerţ" şi alte asemenea - la care fac "matematică" pe 3 ore/săptămână; specific acestor profile este faptul că elevii respectivi - ajunşi iată, în clasa a IX-a - au dificultăţi în a scădea numere de semne contrare, au mari dificultăţi în operarea expresiilor algebrice elementare şi în folosirea egalităţii şi inegalităţii, sunt în imposibilitate de a formula "în cuvinte" relaţii şi corelaţii simple…

Este incredibil cât de puţine şi cât de nesigure cunoştinţe şi deprinderi elementare de geometrie, au putut acumula aceşti elevi în cei trei ani în care au făcut totuşi câte un manual de "geometrie" şi ceea ce mă uimeşte continuu este lipsa de jenă şi nepăsarea generală faţă de situaţia respectivă. Ce vor fi făcut ei (la "geometrie", dar şi pe la "Desen", etc.) dacă în proporţie de masă: nu ştiu să folosească un compas, nu ştiu să construiască mediatoarea unui segment şi de fapt nu ştiu ce-i aceea, după cum nu ştiu sigur nici ce-s acelea mediane, bisectoare, etc.

Fac şi eu ce pot, dincolo de programa şcolară curentă… cred că-i bine, dacă i-am învăţat (pe cât am putut, în primele vreo patru ore) să construiască mediatoarea unui segment, să exprime proprietatea specifică punctelor mediatoarei, să construiască mediatoarele unui triunghi şi cercul circumscris acestuia, să construiască bisectoarea unui unghi, să justifice construcţiile respective, etc.

În acest mediu, cel mai dificil de prins se dovedesc a fi justificările fireşti ale construcţiilor şi mai general, demonstraţiile unora sau altora dintre diversele proprietăţi geometrice sau algebrice (şi însăşi ideea că ar fi ceva de justificat este neaşteptată şi greu de înghiţit). Această dificultate este cu siguranţă urmarea directă a asimilării "practice" a matematicii la nivel de reţetar, sau de "memorator" - ce nevoie să ai de justificări şi demonstraţii ca să iei BAC-ul?!

Totuşi, o pregătire matematică onorabilă nu prea are de-a face cu "memoratorul" şi nici cu învăţarea pe de rost, ci implică inevitabil obişnuinţa derulării unor demonstraţii acceptabile şi căutarea unor justificări şi legături sugestive (necesitând totodată, o bază lingvistică bine dezvoltată).