Prin programul prezentat în [1] am obţinut ciclurile hamiltoniene ale grafului calului pe tabla 6x6 - cam pe durata disputării a vreo două meciuri succesive de tenis: aproape 4.5 ore… Fişierul rezultat (măcar am avut grijă să nu mai includ elemente "informative" - vezi [2]) are exact 9862 de rânduri - ceea ce corespunde valorii indicate în OEIS /A001230; fiecare rând are exact 100 caractere (valori 1..36 cu câte un spaţiu separator), încât rezultatul depăşeşte cu puţin 950 KB.

Am avut curiozitatea de a răsfoi cele 9862 de "pânze" rezultate prin folosirea funcţiei set_canvas() prezentate în [2], încercând să observ direct (fără a face reflecţii suplimentare) configuraţii vizuale semnificative; redăm o serie de pânze, cu diverse aspecte de simetrie:

Ciclurile hamiltoniene (în formă numerică, începând cu 1 în colţul stânga-sus) sunt indicate în atributul "title" (vizibil prin "mouse-over") al fiecărui <canvas>; de fapt, tabloul acestor cicluri şi funcţia set_canvas() folosită aici sunt conţinute în sursa paginii (CTRL+U).

O clasificare elevată (pe concepte sofisticate de simetrie şi de antisimetrie) a acestor cicluri a fost realizată de George Jelliss - Closed Knight's Tours of the 6 by 6 Board.

Trasarea căutării soluţiei (două "linii de control", less şi grep)

Dacă nu eram interesat de transmisiile de tenis, probabil că aş fi întrerupt programul cu mult înainte de încheiere… În fond, puteam încorpora cel puţin acest principiu simplu de restrângere a căutării: dacă la momentul curent există un anumit nod cu un singur adiacent nevizitat - atunci subarborele curent al căutării nu poate conduce la un ciclu hamiltonian şi deci, poate fi abandonat.

Pentru a evidenţia cum se petrec lucrurile (de durează aşa de mult), să revedem metoda din [1] Hamilton::find_path() - intercalând acum două "linii de control" (în fond, banale):

 1
 2
+3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
+21
22
23
24

void Hamilton::find_path(int node, int depth) { // nodul şi adâncimea curente
    path[node] = depth;
std::cout << depth << ":" << node << " "; // nodul curent ("forward")
    if(depth == V) { // dacă s-a trecut prin toate vârfurile
       if(cycle) {
           if(connected(node, start())) { // dacă 'node' este adiacent cu 'start'
               cont++; // contorizează soluţiile obţinute
               dump_path(true); // redă soluţia găsită (ciclu)
           }
       }
       else {
           cont++;
           dump_path(false); // redă soluţia găsită (drum) 
       }
    }
    if(cont < num_sol) { // dacă s-au cerut mai multe soluţii
        reorder(adj[node]); // reordonează adiacenţii nodului curent (Warnsdorff)
        for(auto next: adj[node])
            if(!path[next])
                find_path(next, depth+1); // mecanismul backtracking
std::cout << "\nQ" << node << ' '; // nodul abandonat ("backward", "Quit")
        path[node] = 0; // revine, pentru a încerca altă variantă
    }
}

Linia 3 va afişa adâncimea şi nodul curent explorat, iar linia 21 va afişa nodul de la care nu mai este posibilă extinderea soluţiei parţiale (devenind necesară căutarea unei alte variante, dintr-un nod anterior acestuia). Bineînţeles că vom redirecţiona ieşirea către un fişier text şi nu vom rula programul pentru a obţine toate ciclurile hamiltoniene, ci doar pentru generarea unuia singur.

Reexecutând astfel programul (vezi [1]), rezultă (în 3 minute) un fişier "explore.txt" de aproape 1 GB, conţinând istoria întregului proces de găsire a soluţiei finale. Nu-i cazul să deschidem într-un "editor de text", un fişier aşa de voluminos; pentru început, să folosim programul utilitar clasic less, reţinând numai primele câteva linii:

- Fig. 1 -

0 - 8 - 4 - 17 - 28 - 32 - 24 - 13 - 2...
(colţul 0 devine deja, inaccesibil)

vb@vb:~/KNIGHT$ less explore.txt
1:0 2:8 3:4 4:17 5:28 6:32 7:24 8:13 
   9:2 10:6 11:19 12:30 13:26 14:34 15:21 
  16:10 17:23 18:15 19:11 20:3 21:7 22:18 
  23:31 24:27 25:35 26:22 27:14 28:1 29:9 
  30:5 31:16 32:29 33:33 34:20 35:12 36:25 
Q25 
Q12 
Q20 34:25 35:12 36:20 
Q20 
Q12 
Q25 
Q33 
Q29 32:20 33:12 34:25 35:33 36:29 
Q29 
/* ... */

Prima linie (redată aici pe primele 5 rânduri) arată că la început s-a parcurs liniar (fără vreo revenire) drumul hamiltonian 0 (la pasul 1), 8 (la pasul 2), 4, 17, ..., 13 (la pasul 8), 2, 6, ..., 25 (la ultimul pas - al 36-lea). Apoi, ne-rezultând un ciclu hamiltonian - încep explorările altor ramuri: "Q25" semnifică abandonarea nodului 25 de la pasul anterior 36 (25 nefiind adiacent cu nodul de start).

"Ştergând" muchiile 25-12, 12-20 şi apoi 20 - 33, se ajunge înnapoi la pasul 34 şi se constată (vezi "Q20") posibilitatea 33 - 25 - 12 - 20; aceasta conduce la un nou drum hamiltonian (care coincide până la nodul 33, cu primul drum descoperit); apoi, de pe acest nou drum se şterg succesiv câteva muchii de la sfârşit, revenind (vezi "Q29") la pasul 32 - de unde se avansează pe un nou drum hamiltonian; ş.a.m.d.

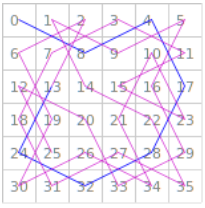
Pe Fig. 1 am marcat primul drum hamiltonian descoperit, marcând cu albastru primele 7 arce ale acestuia: 0-8, 8-4, ..., 24-13. Însă colţul de start 0 are exact doi adiacenţi: nodurile 8 şi 13; deci demarând cu arcul 0-8, ciclul hamiltonian căutat va trebui să se încheie cu arcul 13-0. Prin urmare, arcul 24-13 poate fi cel mult penultimul arc al unui ciclu hamiltonian, iar considerarea continuării 24-13 la pasul 8 trebuia evitată, sistând toate explorările şi reluările de la paşii ulteriori 9, 10, etc.

Pentru a depista momentul în care se revine la pasul 8 pentru a alege altă muchie în loc de 24-13, putem folosi grep:

vb@vb:~/KNIGHT$ grep --byte-offset ' 8:' explore.txt 
0: // offset-ul primei apariţii " 8:"
1:0 2:8 3:4 4:17 5:28 6:32 7:24 8:13 9:2 10:6 11:19 12:30 13:26 14:34 15:21 16:10 
17:23 18:15 19:11 20:3 21:7 22:18 23:31 24:27 25:35 26:22 27:14 28:1 29:9
30:5 31:16 32:29 33:33 34:20 35:12 36:25 
1033378979: // offset-ul celei de-a doua apariţii " 8:" (prima revenire la pasul 8) 
Q13 
8:20 9:31 10:18 11:7 12:3 13:11 14:15 15:2 16:6 17:19 18:30 19:26 20:34 
21:23 22:10 23:21 24:13 25:9 26:5 27:16 28:29 29:33 30:25 31:12 32:1 33:14 
34:27 35:35 36:22 

Constatăm că abandonarea (Q13) subarborelui de căutare cu rădăcina "8:13" se face tocmai pe la sfârşit (ultimul octet al fişierului are offset-ul 1033384306); prin urmare, peste 99% (!) din timpul de execuţie a fost consumat explorând (în mod inutil) toate drumurile care încep cu cele 7 arce marcate cu albastru în Fig. 1.

Putem lista mai departe (folosind grep -A) pentru a vedea cum rezultă în final, ciclul dorit:

vb@vb:~/clasa11/OOP/KNIGHT$ grep --byte-offset -A10 '8:20' explore.txt 
1033378979:Q13 8:20 9:31 10:18 11:7 12:3 13:11 14:15 15:2 16:6 17:19 
               18:30 19:26 20:34 21:23 22:10 23:21 24:13 25:9 26:5 27:16 28:29 
               29:33 30:25 31:12 32:1 33:14 34:27 35:35 36:22 
1033379149-Q22 // abandonează arcul 35-22
1033379154-Q35 // abandonează arcul 27-35
1033379159-Q27 34:22 35:35 36:27 // abandonează 14-27 şi încearcă 14-22
1033379182-Q27 
// ... 

Peste mai puţin de 5000 de octeţi (faţă de Q13) apare în fişier şi rezultatul final (urmare a apelării metodei Hamilton::dump_path(), din linia 13 a metodei find_path() redate mai sus):

vb@vb:~/clasa11/OOP/KNIGHT$ grep --byte-offset '36:13' explore.txt 
1033383878:Q16 25:33 26:25 27:12 28:1 29:14 30:22 31:35 32:27 33:16 34:5 35:9 36:13 
// şi acum este scris ciclul hamiltonian rezultat:
0 8 4 17 28 32 24 20 31 18 7 3 11 15 2 6 21 30 
26 34 23 10 21 29 33 25 12 1 14 22 35 27 16 7 9 13 

Desigur, această metodă de investigare poate fi utilizată pentru analiza oricărui program bazat pe backtracking; programul respectiv trebuie rezumat la un caz tipic (să producă o singură soluţie, nu pe toate) şi trebuie intercalate cele două linii de control menţionate, urmând a folosi pe fişierul rezultat utilitare ca less şi grep, pentru a depista ramificări inutile (de evitat în cursul căutării soluţiei).

Modificarea căutării ciclurilor hamiltoniene pe graful calului

În principiu, modificarea minimă care s-ar impune în baza celor constatate mai sus, ar consta în introducerea liniilor 17-20 din metoda Hamilton::find_path() sub condiţia if(node != 13) - evitând astfel, explorarea inutilă a tuturor drumurilor care trec printr-un nod - 13 sau poate 8, în cazul tablei 6x6 - care de fapt va trebui să încheie ciclul hamiltonian.

Clasele şi metodele din [1] erau totuşi menite pentru a găsi un drum sau un ciclu hamiltonian (eventual, câteva drumuri, sau cicluri), într-un graf oarecare (cu posibilitatea specializării prin derivare). Având acum de găsit precis cicluri şi anume pe toate - renunţăm să mai derivăm din clasele "Hamilton()" şi "Knight()" şi instituim direct:

#include "graph.h"
class Koni: public Graph { // конь (rusă) = cal
public:
    Koni(int n): Graph(n*n), size(n), path(n*n, 0), num_sol(0) { knight_adj(); }
    void find_path() { find_path(0, 1); }
    void dump_path(); 
    int total() { return num_sol; }
private:
    int size;
    Bin path; // ordinea pe traseu a vârfurilor (1..V)
    int num_sol;
    void knight_adj(); // instituie adiacenţa săriturilor calului de şah
    void find_path(int, int); // caută recursiv ciclurile hamiltoniene
    void reorder(Bin&); // reordonează adiacenţii unui nod
};

Copiem pur şi simplu, metoda knight_adj() din definiţia clasei "Knight()" din [1], iar celelalte metode le copiem din definiţia clasei "Hamilton()" - rămânând doar să simplificăm definiţia find_path():

void Koni::find_path(int node, int depth) { // nodul şi adâncimea curente
    path[node] = depth;
    if(depth == V) { // s-a trecut prin toate vârfurile
       if(connected(node, 0)) 
           dump_path(); // redă ciclul găsit
    }
    if(node != 13) { // cazul tablei 6x6
        reorder(adj[node]); // reordonează adiacenţii (Warnsdorff)
        for(auto next: adj[node])
            if(!path[next])
                find_path(next, depth+1); // mecanismul backtracking
        }
    path[node] = 0; // caută altă variantă
}

Apoi, pentru a obţine ciclurile hamiltoniene (pe tabla 6x6) putem formula:

#include "koni.h"
#include <iostream>
int main() {
    Koni K(6);
    K.find_path();
    std::cout << K.total();
}
// g++ --std=gnu++0x -O2 -o koni koni_1.cpp koni.cpp graph.cpp

Executând acest program (cu redirectare pe un fişier text), obţinem rezultatul (cele 9862 de cicluri hamiltoniene ale grafului calului pe tabla 6x6) în circa 45 de minute - ceea ce este totuşi, de 6 ori mai convenabil decât timpul de 4.5 ore în care obţinusem iniţial, acest rezultat.

Desigur, dacă ne gândim şi la tabla 8x8 - atunci mai trebuie făcute nişte adaptări (de exemplu, nodul "13" devine 1+2*8=17) şi eventual, avem de căutat măcar încă un criteriu (dar cât mai simplu) care să permită restrângerea şi mai mult, a căutării ciclurilor pe graful calului.