Modelul ArTree din [1] serveşte pentru a institui în cursul unui program arbori sintactici de expresii aritmetice (fără să pretindă existenţa prealabilă a unui format textual explicit al expresiei) - servind astfel pentru generarea tuturor expresiilor aritmetice de o formă sau alta:

char oper[] = {'+', '-', '*', '/', '^'}; 
int numb[] = {1,3,4,6}; // operanzii daţi
ArTree h = ArTree( o1,  // rădăcina arborelui (_root); o1, o2, o3 ∈ oper[]
               ArTree(o2, numb[0], numb[1]),   // subarborele stâng (left)
               ArTree(o3, numb[2], numb[3]) ); // subarborele drept (right)

Variind o1, o2, o3 în oper[] şi permutând numb[], vom obţine toţi arborii aritmetici posibili care în exprimare textuală obişnuită au forma (A o2 B) o1 (C o3 D) - unde A..D ∈ numb[]; tocmai aceasta face funcţia phrase() din [2] (în care acum, trebuie înlocuit "Tree" cu "ArTree").

Promovând scopul de a genera expresiile de un anumit tip şi având în vedere numărul mare al lor - este firesc să fi căutat o constituire cât mai "economică" pentru ArTree. Dar omiţând încărcarea cu obişnuitele metode publice de acces la membri, arborele (odată instanţiat din ArTree) devine un tot indivizibil: nu-i putem accesa subarborii - membrii _root, left şi right fiind calificaţi cu private.

În [1] am imaginat cam singura extensie plauzibilă, constând în derivarea clasei Climb - permiţând instanţierea acelui obiect ArTree (indivizibil) care corespunde unei expresii aritmetice date. O altă extindere ar viza vizualizarea - dar aceasta nu poate fi realizată direct (urmând de exemplu modelul din [3]), arborele respectiv (odată creat) neputând fi traversat.

Totuşi, descrierea arborelui sintactic în limbajul DOT se poate obţine şi fără a traversa direct arborele respectiv; vom arăta mai jos un algoritm foarte simplu, plecând de la forma prefixată a expresiei:

#include "infix.h" // vezi [1]
#include <sstream> // şi încă: <iostream>, <fstream>, <string>

int main(int argc, char** argv) { // ./ast "(2.55 + 3.15/ 2 ^ 2.5 + 7.25) * 4.456"
    Climb expr;
    ArTree::set_format(0);   // formatul prefixat
    std::ostringstream buff;
    try {
          buff << expr.get_tree(argv[1]);
          to_DOT(buff.str(), "artree.dot"); // exprimă arborele în limbajul DOT
    } catch(const char* error) { // expresia dată este incorectă sintactic 
        std::cout << error << '\n';
    }
}

Programul redat mai sus preia de pe linia de comandă o expresie aritmetică (în format infixat) şi foloseşte metoda Climb::get_tree() din [1] - obţinând arborele sintactic ArTree corespunzător expresiei date; apoi, prin intermediul metodei operator<< redefinite de ArTree - inserează în buff reprezentarea textuală prefixată a arborelui obţinut. În final, funcţia to_DOT() va analiza această reprezentare, producând un fişier ("artree.dot") care conţine descrierea DOT a arborelui.

Algoritmul pe care se bazează to_DOT() ar necesita o mică adaptare faţă de [1], privitoare la formatul prefixat:

void Operator::print(std::ostream& out) const { 
    switch(ArTree::format) {
        case 1: // infixat
            /* ... */
        case 2: // postfixat
            /* ... */
        default: // prefixat - în [1]: out<<' '<<binop<<' '<< left<<' '<< right;
            out << binop << "("<< left << "," << right << ")" ;
    }
}

De exemplu, "6 / (1 - 3/4)" va fi redată acum sub forma "/(6,-(1,/(3,4)))" (în loc de "/ 6 - 1 / 3 4") - parantezând subarborii şi separând prin virgulă subarborele stâng de cel drept; dar acest format de redare prefixată nu este nicidecum nou, fiind utilizat "nativ" de predicatul write_canonical/1 din sistemele Prolog (vezi [4]).

Obţinerea descrierii DOT (într-un fişier text) se bazează astfel, pe următoarele elemente:

1— Parcurgem expresia furnizată ca parametru - în formatul prefixat canonic - de la stânga spre dreapta; când caracterul curent este o cifră, îl inserăm înnapoi în şir şi extragem în loc operandul numeric anticipat de acea cifră.

2— Pe măsură ce parcurgem expresia - numerotăm nodurile arborelui, imitând metoda clasică de reprezentare pe un tablou a unui arbore binar: dacă rădăcina are indexul K, atunci fiul stâng va avea indexul 2K, iar cel drept 2K+1 (K ≥ 1). Pentru nodul curent K înscriem în fişier o înregistrare DOT de forma K [label="op"], op fiind operatorul sau operandul reprezentat de nodul numerotat K.

3— De fiecare dată când caracterul curent este '(' - dublăm valoarea curentă K (obţinând numărul nodului corespunzător fiului stâng al lui K) şi înscriem în fişier înregistrarea DOT a muchiei: K/2 -- K.

4— Când caracterul curent este ',' - incrementăm valoarea curentă K (obţinând numărul nodului corespunzător fiului drept al lui K) şi înscriem în fişier înregistrarea DOT a muchiei: K/2 -- K.

5— De fiecare dată când caracterul curent este ')' - înjumătăţim valoarea curentă K, ajungând la părintele lui K (de unde va urma eventual, o nouă ramificare - de exemplu prin pasul 4).

Pentru algoritmul 1..5 descris mai sus avem imediat următoarea implementare:

void to_DOT(std::string pexpr, std::string filename) {
    std::istringstream pref(pexpr);
    std::ofstream out(filename.c_str());
    out << "/*\n\t" << pexpr << "\n*/\n"; // documentează expresia reprezentată în fişier
    out << "graph G {\n"; // specificaţia DOT pentru un graf neorientat
    out << "node[shape=plaintext, fontsize=16]\n"; // atributele nodurilor (global)
    char c;
    int K = 1; // începe numerotarea nodurilor
    while(pref >> c) { // extrage câte un caracter, de la stânga spre dreapta
        if(c>='0' && c <='9') { // semnalează "operand numeric" - vezi pasul 1 
            pref.putback(c); // reînscrie cifra iniţială a operandului
            double number;
            pref >> number; // extrage operandul
            out << K << "[label=\"" << number << "\"]\n"; // vezi pasul 2
            continue; // reia bucla, citind următorul caracter
        }
        switch(c) {
            case '(':  // vezi pasul 3
                K <<= 1; // dublează valoarea ("shift-left 1")
                out << K/2 << "--" << K << '\n';
                break;
            case ',':  // vezi pasul 4
                K += 1;
                out << K/2 << "--" << K << '\n';
                break;
            case ')':  // vezi pasul 5
                K >>= 1; // înjumătăţeşte valoarea ("shift-right 1")
                break;
            default:
                out << K << "[label=\"" << c << "\"]\n";  // vezi pasul 2
                break;
        }
    }
    out << '}'; // încheie descrierea DOT a arborelui
}

Este evident acum că to_DOT() este o funcţie independentă de ArTree: poate fi apelată din orice program (nu neapărat din cel specificat la început, care includea definiţia ArTree) - dar cu condiţia ca expresia specificată drept parametru să fie scrisă neapărat în formatul prefixat (din Prolog) pe care mizează algoritmul de mai sus (şi să fie corectă sintactic, fiindcă to_DOT() nu face verificări).

Dar adăugând to_DOT() în programul redat la început, putem specifica expresia în formatul obişnuit (infixat); putem executa de exemplu ./ast "(2.55 + 3.15/ 2 ^ 2.5 + 7.25) * 4.456" - obţinând fişierul ("artree.dot", specificat în apelul funcţiei to_DOT() din programul indicat):

/*
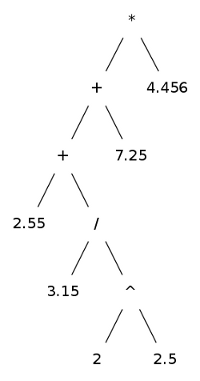
    *(+(+(2.55,/(3.15,^(2,2.5))),7.25),4.456)
*/
graph G {
    node[shape=plaintext, fontsize=16]
    1[label="*"]
    1--2
    2[label="+"]
    2--4
    4[label="+"]
    4--8
    8[label="2.55"]
    4--9
    9[label="/"]
    9--18
    18[label="3.15"]
    9--19
    19[label="^"]
    19--38
    38[label="2"]
    19--39
    39[label="2.5"]
    2--5
    5[label="7.25"]
    1--3
    3[label="4.456"]
}

Pentru a obţine şi imaginea corespunzătoare fişierului DOT rezultat, putem folosi programul utilitar dot, invocându-l prin dot -Tpng -o artree.png artree.dot. Desigur, în prealabil am putea modifica fişierul DOT obţinut - de exemplu, înlocuind shape=plaintext cu shape=circle, sau specificând alt fontsize, sau anumite culori pentru muchii, etc.; dar nu-i de dorit schimbarea ordinii înregistrărilor - este necesar să se respecte regula ca înregistrarea corespunzătoare subarborelui stâng să apară neapărat înaintea celei aferente subarborelui drept (altfel arborele va apărea "inversat").

Imaginea poate fi afişată imediat pe ecran, folosind de exemplu programul utilitar display (din ImageMagick): display artree.png.