Când am nevoie de figuri, folosesc MetaPost (sau R); reluând din când în când tutorialele disponibile, am întâlnit unele programe care merită (cu prisosinţă) să fie analizate, corelate (inclusiv, cu ceva matematică) şi eventual, dezvoltate.
Secţiunea "Transformations" din André Heck - Tutorial in MetaPost (sau "Learning MetaPost by Doing") se încheie cu următorul exemplu ("playful"):

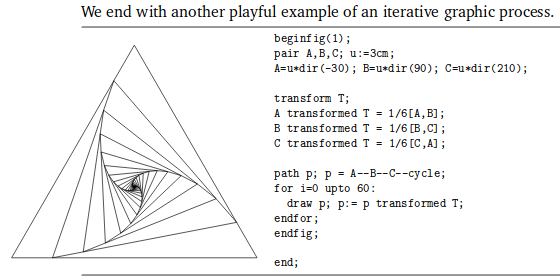
Pe laturile unui triunghi echilateral se consideră (într-un acelaşi sens de rotaţie) punctele care le împart într-un acelaşi raport fixat; pe triunghiul echilateral rezultat se aplică aceeaşi construcţie, iterând procesul de câte ori s-ar dori.

Odată definite punctele $\small A$, $\small B$ şi $\small C$, se consideră conturul închis al acestora path p; p = A -- B -- C -- cycle şi i se aplică succesiv transformarea $\small \mathsf{T}$ (prin p := p transformed T) care modelează construcţia indicată mai sus (plotând totodată fiecare contur p).
MetaPost consideră (prin transform T) transformări liniare (generale) $$\small \mathsf{(x,y)\mapsto (t_{xx}x+t_{xy}y+t_x,\,t_{yx}x+t_{yy}y+t_y)}$$ şi dacă îi sunt precizate imaginile prin $\small \mathsf{T}$ a trei puncte cunoscute, compilatorul va putea determina cei şase coeficienţi $\small \mathsf{t_{xx}}$, $\small \mathsf{t_{xy}}$, etc. (rezolvând intern ecuaţiile liniare asociate; iar coeficienţii pot fi referiţi prin xxpart T, xypart T, ş.a.m.d.).

Dar ecuaţiile specificate în program (A transformed T = 1/6[A,B]; şi celelalte două) conduc evident la un triunghi asemenea cu $\small\Delta ABC$ (fiindcă transformatele împart în acelaşi raport (= 1/6) laturile [A,B], [B,C], [C,A]). Ori asemănarea este totuşi un caz particular de transformare liniară, implicând - cum am observat în [1] - egalităţile $\small\mathsf{t_{xx}=t_{yy},\,t_{xy}=-t_{yx}}$; prin urmare, pentru a defini $\small\mathsf{T}$ (ca asemănare) sunt suficiente două ecuaţii (în loc de trei, ca în cazul general) - iar această observaţie sugerează o abordare mai generală, a procesului iterativ descris prin programul redat mai sus.

Să considerăm un poligon regulat oarecare; prin rotire şi scalare îl putem identifica cu poligonul constituit de rădăcinile de ordinul $n$ ale unităţii ($n\ge 3$ fiind numărul de vârfuri dorit) - încât afixele vârfurilor sunt $w_k=e^{i2k\pi/n},\,\small k=0..n-1$, sau în notaţii specifice MetaPost: pair w; w[k] = dir(360k/n).
(Unghiurile se măsoară în grade, nu în radiani; operatorul dir furnizează versorul direcţiei indicate - de exemplu, dir(30) ne dă punctul (cos 30, sin 30)=(0.86603, 0.5).)

Pentru a constitui un poligon asemenea celui considerat şi care să aibă vârfurile pe laturile acestuia, putem defini o asemănare $\small\mathsf{T}$ care să transforme $w_0$ şi $w_1$ în punctele care împart laturile $\overline{w_0w_1}$ şi respectiv $\overline{w_1w_2}$ într-un acelaşi raport fixat $\lambda$; noul poligon va rezulta aplicând $\small\mathsf{T}$ conturului iniţial.

Un program monolitic (precum cel redat mai sus) ar fi mai scurt ca formulare, dar vizând diverse experimente este preferabil să definim separat lucrurile (polygon(), similarity(), iterate()) implicate în construirea figurii respective:

%%% 3demo.mp %%%  % [ outputformat:="png"; outputtemplate:="%j-%c.png"; ] %

vardef polygon(expr n, u) =
    save p; path p[];
    for k=0 upto n-1:
        p[k] = u*dir(360k/n);  % 'u' este unitatea de măsură (ex. u=3cm)
    endfor;
    for k=0 upto n-1:
        p[k] -- endfor cycle
enddef;  %% returnează conturul închis al rădăcinilor de ordinul n ale unităţii

vardef similarity(expr p, ratio) =
    save T; transform T;
    xxpart T = yypart T; xypart T = -yxpart T;
    pair A[]; for i=0 upto 2:
        A[i] = point i of p;
    endfor;
    A0 transformed T = (ratio)[A0, A1];
    A1 transformed T = (ratio)[A1, A2];
    T
enddef;  %% T(p) va fi un contur asemenea cu 'p', cu vârfurile pe laturile lui 'p'

vardef iterate(expr n, unit, ratio, iter) = 
    image(
        path p; p = polygon(n, unit*cm);
        transform T; T = similarity(p, ratio);
        for i=0 upto iter:
            draw p;
            p := p transformed T;
        endfor;
    )        
enddef;  %% iterează asemănarea cu un poligon dat şi returnează imaginea finală

beginfig(1);
    drawoptions( withpen pencircle scaled 7/8 );
    picture d[];  d0 = iterate(4, 4, 1/6, 20);  draw d0;
    d1 = iterate(5, 4, 1/6, 30);
    d2 = iterate(6, 4, 1/6, 40);
    draw d1 shifted(2*xpart(lrcorner d0)-.5cm, 0);
    draw d2 shifted(4*xpart(lrcorner d0)-.25cm, 0);
    drawoptions();
endfig;

end

Pentru o prima figură am considerat $n$=4, 5, respectiv 6 şi $\lambda=1/6$, iterând de 20, 30, respectiv 40 de ori şi am aliniat orizontal imaginile respective:

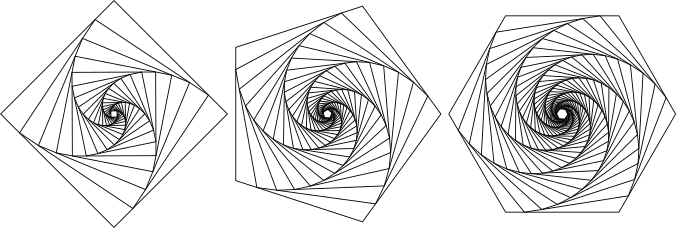
Am adăugat o a doua figură, pentru care am ales $\lambda=.5$ (cu 10 iteraţii), respectiv $1/3$ (cu 16 iteraţii); poligoanele se disting astfel mai bine:

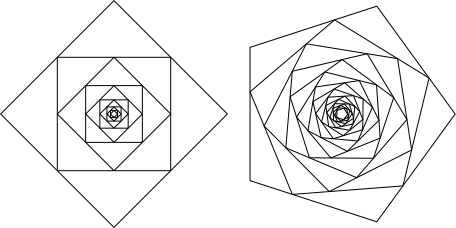
Pentru o a treia figură, am copiat definiţia iterate() în iterate_(), în care am înlocuit "draw p;" prin "draw point 0 of p withpen pencircle scaled 2;" - încât (invocând acum - spre deosebire de figurile precedente - iterate_() în loc de iterate()) să evidenţiem cumva traseul descris de un vârf pe parcursul iterărilor (am vizat vârful 0 şi am ales $\lambda$ mic, 0.1 şi respectiv 1/8; am iterat de un număr rezonabil de ori - 30 şi respectiv 32):

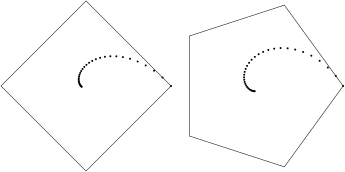
Din figurile obţinute astfel, ne dăm seama că pe parcursul iterărilor fiecare vârf se află pe câte o anumită spirală, depinzând de $n$ şi de $\lambda$. Să încercăm să lămurim "teoretic" lucrurile.

Orice vârf al poligonului regulat curent (rezultat în iteraţia curentă) se poate obţine din vârful care îl precede în acest poligon printr-o rotaţie de unghi $2\pi/n$. Să considerăm vârful $z_0=1$ şi fie $w_0=e^{i2\pi/n}$ vârful următor lui $z_0$ în poligonul iniţial. După prima iteraţie, $z_0$ ajunge în punctul $z_1$ care împarte latura $\overline{z_0w_0}$ în raportul $\lambda\in(0,1)$; deci $z_1=(1-\lambda)z_0+\lambda w_0=1-\lambda+\lambda e^{i2\pi/n}$. Vârful $w_1$ următor lui $z_1$ pe poligonul curent, se obţine din $z_1$ printr-o rotaţie de unghi $2\pi/n$, deci $w_1=z_1 e^{i2\pi/n}$; prin următoarea iteraţie, $z_1$ ajunge în punctul $z_2$ care împarte latura $\overline{z_1w_1}$ în raportul $\lambda$ - deci $z_2=(1-\lambda)z_1+\lambda w_1{\small=(1-\lambda)z_1+\lambda z_1 e^{i2\pi/n}=z_1(1-\lambda+\lambda e^{i2\pi/n})}=z_1^2$.

Prin inducţie rezultă că după $k\ge 0$ iteraţii, vârful $z_0$ ajunge în punctul de afix $$z_k=z_1^k=\left(1-\lambda+\lambda e^{i2\pi/n}\right)^k\quad\quad\quad(1)$$ Dar avem acest rezultat general (cunoscut): progresia geometrică $(u^n)_{n\ge 0}$, cu $u\in\mathbb{C}^*$, este situată pe o spirală logaritmică. Într-adevăr, ecuaţia unei spirale logaritmice (modelând faptul că raza polară creşte - sau descreşte - mereu (în progresie geometrică), pe măsură ce punctul se roteşte în jurul originii) este de forma $z(t)=e^{Kt} e^{it}$ cu $t\in\mathbb{R}$ (unde $\small K$ este un factor constant). Având în vedere definiţia pentru logaritm complex, putem scrie: $u^n=e^{n\log u} = e^{n(\log|u|+i\,\arg u)}$ şi egalând cu $e^{({\small K}+i)t}$ avem ${\small K}t=n\log |u|$ şi $t=n\arg u$ - de unde găsim ${\small K}=\log|u|/\arg u$ (deci $u^n$ aparţine spiralei logaritmice corespunzătoare acestui $\small K$).

Aplicând acest rezultat progresiei geometrice (1), deducem că punctele $z_k$ se află pe spirala logaritmică $z(t)=e^{Kt}e^{it},\,t\ge 0$ cu ${\small K}=\log|z_1|/\arg z_1$, unde avem de mai sus $z_1=1-\lambda+\lambda e^{i2\pi/n}$.

Dacă vrem să probăm, cel mai indicat este să folosim R (în care se lucrează lejer cu funcţii de variabilă complexă):

progression <- function(u, k)  u^k
spiral <- function(u, t)  exp(t*log(abs(u))/Arg(u)) * exp(1i*t)

the_u <- function(n, l)  1 - l + l*exp(1i*2*pi/n)
seq_t <- seq(-0.25, 20, by=0.01)

iterate <- function(n, l, col=c("red", "blue")) {
    u <- the_u(n, l)
    points(progression(u, 0:35), pch=20, cex=0.5, col=col[1])  # z_0..z_35 din (1)
    points(spiral(u, seq_t), type="l", col=col[2])  # spirala logaritmică (fragment)
}

plot(spiral(the_u(5, 1/6), seq_t), type="n",   # doar setează fereastra grafică
     asp=1, bty="n", cex.axis=0.8, xlab="", ylab="");  grid()

iterate(5, 1/4)  # pentru pentagonul regulat
iterate(4, 1/5, col=c("black", "darkgreen"))  # pentru pătrat

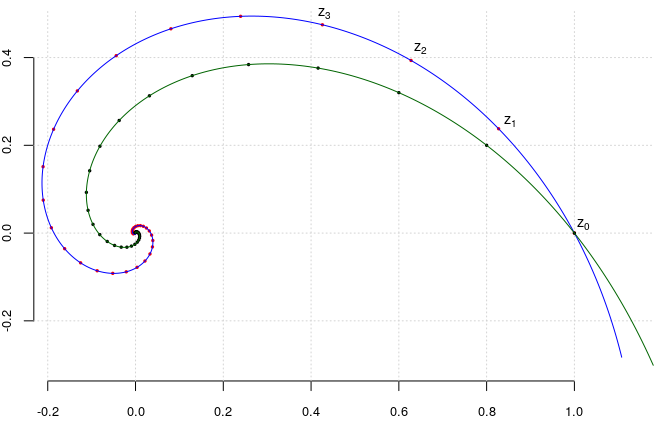
Am plotat câte un fragment din spiralele corespunzătoare pentru $n=5,\,\lambda=1/4$ şi respectiv $n=4,\,\lambda=1/5$, marcând câte un anumit număr de puncte date de (1).

Revenim acum la programul "3demo.mp" redat mai sus, pentru a adăuga o figură în care exploatăm facilitatea de a combina imaginea curentă (reprezentată în memorie de structura de date currentpicture) cu simetrica ei faţă de o linie sau alta:

beginfig(5);
    picture d[];  d0 = iterate(4, 4, 1/18, 52) rotated 45;
    draw d0;
    draw d0 reflectedabout(llcorner(d0), lrcorner(d0));
    addto currentpicture also 
          currentpicture reflectedabout(urcorner(d0), lrcorner(d0));
endfig;

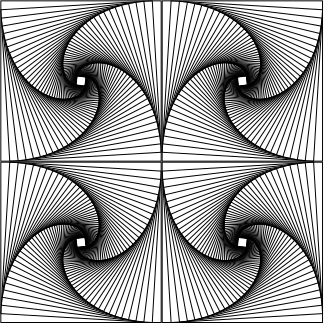
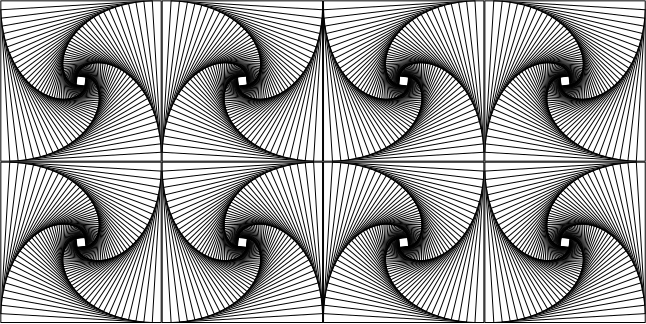
Am iterat pentru $n=4$ şi am rotit cu 45 grade, apoi am simetrizat faţă de dreapta care uneşte colţurile de jos ale pătratului şi în final, am simetrizat imaginea rezultată faţă de linia care uneşte colţurile din dreapta ale pătratului. Bineînţeles că putem aplica acelaşi procedeu imaginii rezultate (cea redată mai sus în stânga), obţinând de exemplu imaginea redată în partea dreaptă (dar precizăm că imagini de acest gen apar în diverse alte locuri; de exemplu, v. pursuit curves).