Amintim că produsul $z_1z_2$ a două numere complexe are ca modul $|z_1||z_2|$ (produsul modulelor factorilor) şi ca argument ${\rm{arg}}\,z_1+{\rm{arg}}\,z_2$ (suma argumentelor factorilor). În particular, $iz$ (înmulţirea cu $i$) revine la rotirea punctului (de afix) $z$ în jurul originii, în sens antiorar, cu unghiul ${\rm{arg}}(i)=\pi/2$; deci punctele $z$, $iz$ şi $\small\mathsf{O}(0,0)$ formează un triunghi dreptunghic isoscel - încât am putea spune că valoarea ${i}$ caracterizează triunghiurile dreptunghice isoscele: raportul catetelor este 1 (=$|i|$), iar unghiul $\pi/2$ al catetelor este dat de ${\rm{arg}}(i)$.

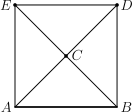Un pătrat împreună cu diagonalele sale evidenţiază 8 triunghiuri dreptunghice isoscele. Dacă referim planul complex la centrul $\small C(0,0)$ al pătratului, atunci vârfurile consecutive în sens antiorar ale acestuia se obţin plecând de la afixul $z$ al unui vârf fixat şi înmulţindu-l la fiecare pas cu $i$ (dacă $A(z)$, atunci $B(iz)$, $D(i^2z)$ şi $E(i^3z)$).
Observăm că avem câte trei triunghiuri dreptunghice isoscele (deci, asemenea între ele) care au în comun o aceeaşi latură a pătratului; de exemplu, pe latura $\small AB$ avem $\small \Delta ABC \sim \Delta BEA \sim \Delta DAB$ (vârfurile sunt notate totdeauna în sens antiorar şi ţinând seama de egalităţile de unghiuri corespondente).
Dacă "deformăm" figura, considerând un patrulater oarecare $\small ABDE$ şi păstrând asemănarea cu un triunghi dat a triunghiurilor formate pe latura $\small AB$ - atunci, va rămâne asemenea triunghiului dat şi $\small \Delta DEC$ (format de vârfurile opuse laturii comune)?

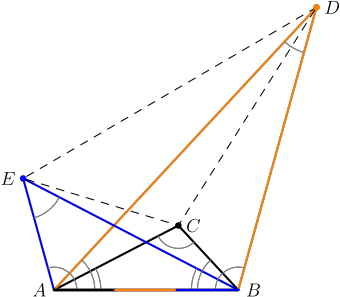
Triunghiurile construite pe latura comună $\small AB$ (conturate pe imaginea redată mai sus respectiv cu negru, orange şi albastru) sunt asemenea unui triunghi $\small \mathsf{XYZ}$ dat; atunci… avem şi asemănarea $\small \Delta DEC \sim \Delta \mathsf{XYZ}$.

Să observăm că $\small BD$ şi $\small AE$ sunt egal înclinate faţă de $\small AB$ şi la fel sunt $\small BC$ şi $\small AD$; deci dacă $\small C_1$ şi $\small C_2$ sunt intersecţiile mediatoarei segmentului $\small AB$ cu $\small BC$ şi respectiv cu $\small AC$, atunci obţinem $\small D$ şi $\small E$ intersectând $\small AC_1$ şi $\small BC_2$ cu dreapta prin $\small B$ şi respectiv prin $\small A$ care face cu $\small AB$ un unghi egal cu unghiul $\small C$ din $\small \Delta ABC$. Deci o construcţie "interactivă" (cu creionul, rigla şi compasul sau, de exemplu cu GeoGebra) a figurii - presupunând dat $\small \Delta ABC$ - se poate face astfel: construim mediatoarea lui $\small AB$ şi marcăm intersecţiile $\small C_1$ şi $\small C_2$ (cu $\small BC$ şi $\small AC$); măsurăm unghiul din $\small C$ şi trasăm dreptele prin $\small B$ şi $\small A$ înclinate cu acest unghi faţă de $\small AB$; apoi marcăm intersecţiile acestor drepte cu $\small AC_1$ şi respectiv $\small BC_2$ (găsind $\small D$ şi $\small E$).

Toate triunghiurile care sunt asemenea între ele au o aceeaşi 'formă' (la fel cum figurile "d" şi "p" au aceeaşi formă - obţinându-se una din alta prin rotaţie, scalare şi translaţie). Forma triunghiului $uvw$ (caracterizând toate triunghiurile asemenea lui) poate fi exprimată prin numărul complex $\dfrac{u-w}{u-v}$: modulul acestuia ne dă raportul laturilor $\vec{uw}$ şi $\vec{uv}$, iar argumentul lui ne dă unghiul format de aceste laturi (astfel că "forma" $\frac{u-w}{u-v}$ reflectă condiţia de asemănare a triunghiurilor: să se păstreze raportul a două laturi, împreună cu unghiul acestora). De exemplu, regăsim "caracteristica" $i$ pe care o vizasem direct, la început: triunghiurile dreptunghice isoscele (şi la fel orientate) au forma $\frac{0-i}{0-1}=i$ (am luat $\Delta uvw$ cu $u=0$, $v=1$ şi $w=i$).

Forma triunghiurilor a fost introdusă de J. A. Lester (1996) "Triangles I: Shapes", Aequationes Mathematicae 52 (unde am găsit şi problema pe care o tratăm aici).

Notând cu $\lambda$ forma triunghiului dat $\small \mathsf{XYZ}$ (şi cu litere mici omonime, afixele vârfurilor), pentru cele trei triunghiuri asemenea acestuia ridicate pe latura comună $\small AB$ (v. figura de mai sus), avem: $$\frac{a-c}{a-b}=\frac{b-a}{b-e}=\frac{d-b}{d-a}=\lambda$$

Rezultă că $c=a-\lambda(a-b)$, $e=b+(a-b)/\lambda$ şi $d=(b-\lambda a)/(1-\lambda)$; acum putem calcula "caracteristica" triunghiului $\small \Delta DEC$ şi obţinem $\frac{d-c}{d-e}=\lambda$, însemnând că avem într-adevăr, $\small \Delta DEC \sim \Delta \mathsf{XYZ}$ (au aceeaşi formă).

Am obţinut figura de mai sus folosind MetaPost, ca şi în [1] (desigur, mai potrivit ar fi R, în care putem lucra comod cu numere complexe şi este uşor de modelat transformările geometrice de care ar fi nevoie, având asigurată în plus o precizie de calcul "mai bună").
Se poate observa întâi, că am marcat unghiurile prin anumite arce de cerc (proporţionând cumva raza după mărimea unghiului); în acest scop am introdus următoarele definiţii:

vardef acosd primary x = angle (x, 1 +-+ x) enddef;

def markang(expr A, O, B) = 
    save m;
    m = acosd (((A-O) dotprod (B-O)) / (abs(A-O)*abs(B-O)));  % show(m);
    draw subpath(0, m/45) of fullcircle 
                          scaled ((180-m)/120*u) 
                          rotated (angle(B-O)) 
                          shifted O 
         withcolor 0.5white;
enddef;

def marktriang(expr A, B, C) =
    markang(A, B, C);
    markang(B, C, A);
    markang(C, A, B);
enddef;

angle(x,y) dă (în grade, nu radiani) unghiul vectorului de poziţie a punctului indicat; "+-+" este operatorul definit prin $\small a$ +-+ $\small b\equiv\sqrt{a^2-b^2}$. Deci acosd(x) definit mai sus determină (pentru $\rm|x|\le 1$) valoarea $\small \rm{arctg}\,\frac{\sqrt{1-x^2}}{x}=\rm{arccos}\,x$ (în grade). Calculele comportă desigur o anumită aproximare; de exemplu, folosind show(acosd(-0.5)) obţinem 119.99992 (în loc de valoarea exactă de 120 grade).

Cosinusul unghiului a doi vectori este dat de raportul dintre produsul scalar (care se obţine prin dotprod) şi produsul lungimilor acestora; în markang() am folosit acosd pentru a determina unghiul $\small\measuredangle{AOB}$ (=$\small\rm arccos\,\frac{\vec{OA}\cdot\vec{OB}}{|\vec{OA}|\,|\vec{OB}|}$) şi am considerat (prin subpath) arcul cercului unitate corespunzător acestui unghi; am scalat cumva acest arc după mărimea unghiului, l-am rotit în jurul originii încât raza iniţială să treacă prin $\small B$ şi în final, am translatat arcul încât să aibă centrul în vârful unghiului care trebuie marcat. Apoi, marktriang() expandează markang() pentru a marca fiecare dintre unghiurile unui triunghi dat.

Considerăm un triunghi $\small \mathsf{XYZ}$ şi deocamdată, să testăm folosirea definiţiilor de mai sus, înfiinţând temporar o figură (cu numărul 95 să zicem):

vardef XYZ =
    (1, 2)*u -- (5, 4)*u -- (3, 4.75)*u -- cycle
enddef;

beginfig(95);
    save u, p, v; u = 1cm;
    path p;  p = XYZ;
    pair v[]; 
    for i=0,1,2:
        v[i] = point i of p;
    endfor;
    draw p withpen pencircle scaled 0.8;
    marktriang (v0, v1, v2);
    label.lft(btex $X$ etex scaled 0.7, v0);
    label.rt(btex $Y$ etex scaled 0.7, v1);
    label.top(btex $Z$ etex scaled 0.7, v2);
    currentpicture := currentpicture scaled 2;
endfig;

Urmează o descriere (liniară, deci lungă) a construcţiei triunghiurilor asemenea lui $\small \mathsf{XYZ}$ care au o latură comună dată: se defineşte pentru fiecare caz o variabilă de tip transform (ca în [1]) care să mapeze câte o latură din $\small \Delta \mathsf{XYZ}$ pe latura comună indicată şi se determină imaginea vârfului rămas; se trasează contururile rezultate şi în final, se marchează şi se etichetează elementele figurii:

def similar(expr a, b) = 
    save v, w, p;
    transform T[]; pair v[], w[]; path p[];
    for i=0,1,2:
        v[i] = point i of XYZ;
    endfor;
    for i=0,1,2:  % condiţiile pentru "asemănare" (v. [1])
        xxpart T[i] = yypart T[i];
        xypart T[i] = - yxpart T[i];
    endfor;
    v0 transformed T0 = a;
    v1 transformed T0 = b;
    w0 = v2 transformed T0;
    p0 = a -- b -- w0 -- cycle;
    v1 transformed T1 = a;
    v2 transformed T1 = b;
    w1 = v0 transformed T1;
    p1 = w1 -- a -- b -- cycle;
    v2 transformed T2 = a;
    v0 transformed T2 = b;
    w2 = v1 transformed T2;
    p2 = b -- w2 -- a -- cycle;
    p3 = w1 -- w2 -- w0 -- cycle;
    drawoptions (withpen pencircle scaled 0.8);
    draw p0 withcolor .5black;
    draw p1 withcolor orange;
    draw p2 withcolor blue;
    draw p3 withpen pencircle scaled 0.4 dashed evenly;
    drawoptions(withpen pencircle scaled 2.5pt);
    drawdot w0 withcolor .5black;  % marchează vârfurile opuse laturii comune
    drawdot w1 withcolor orange;
    drawdot w2 withcolor blue;
    drawoptions (withpen pencircle scaled 0.4);
    for i=0,1,2:  % marchează unghiurile corespondente ale triunghiurilor
        marktriang (point 0 of p[i], point 1 of p[i], point 2 of p[i]);
    endfor;
    drawoptions(withpen pencircle scaled 1);
    for i=0 step 3 until 2:  % sugerează "latura comună" a trei triunghiuri
        draw (i/3)[a, b] -- ((i+1)/3)[a, b] withcolor 0.5black;
        draw ((i+1)/3)[a, b] -- ((i+2)/3)[a, b] withcolor orange;
        draw ((i+2)/3)[a, b] -- ((i+3)/3)[a, b] withcolor blue;
    endfor;
    label.lft(btex $A$ etex scaled 0.6, a);
    label.rt(btex $B$ etex scaled 0.6, b);
    label.rt(btex $C$ etex scaled 0.6, w0);
    label.rt(btex $D$ etex scaled 0.6, w1);
    label.lft(btex $E$ etex scaled 0.6, w2);
enddef;

Rămâne să definim o figură în care să folosim similar():

beginfig(1);
    save u, a, b; u = 1cm;
    pair a[]; a0 = origin*u; a1 = 2.5u*right;
    similar(a0, a1);
    currentpicture := currentpicture scaled 2.6;
endfig;

Învocând compilatorul de MetaPost (prin mpost -tex=latex 1demo.mp; v. [1]), obţinem fişierul "1demo-1.png" redat de două ori (ca imagine) mai sus.