Deducerea încadrării, de pe "Orarul general clase"
Există diverse posibilităţi, pentru a „anonimiza” numele profesorilor; cea mai simplă constă în a le omite – nu-ţi trebuie nici ştiinţă, nici ingeniozitate, nici bun-simţ.
Avem un "Orarul general clase", produs prin "aSc Orare"/ascTimeTables: pentru fiecare clasă, ştim obiectul (abreviat acceptabil) pentru lecţia din fiecare zi şi oră; cine şi la care clase face obiectul respectiv – a devenit secret.
Nu ne pasă de numele profesorilor ci doar, la care clase are ore fiecare (abreviat acceptabil); de ce ne interesează „la care clase are ore fiecare ”? — bună întrebare…;
a căuta „De capul meu prin problema orarului şcolar” (Google Play; 130p., 100lei).
Bunul-simţ ne spune că nu vom putea reconstitui încadrarea profesorilor; dar putem deduce nişte încadrări plauzibile şi avem de imaginat cum anume.
Implicit, rezultă acest aspect „practic”: dacă ai deja un orar pe obiecte bun, atunci poţi face aproape automat, o încadrare a profesorilor pe clase pentru următorul an şcolar (şi pentru următorii), care să corespundă orarului existent!
De la celule aliniate, la date
Căutăm o şcoală oarecare şi descărcăm "Orarul general clase" (dar nu chiar „oarecare” – am căutat una cu multe clase, funcţionând într-un singur schimb):
vb@Home:~/22mai$ wget https://liis.ro/hosted/activitati/2021/orar/orar.pdf .
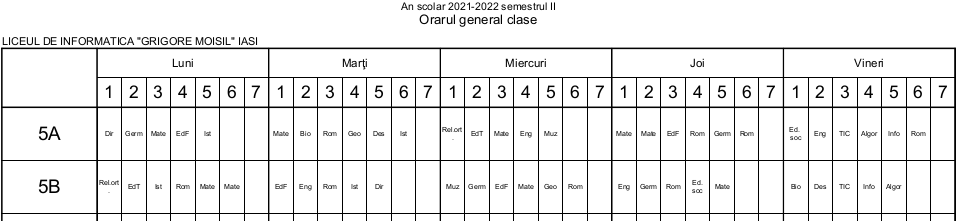
Prima pagină începe cu titlul documentului, centrat orizontal; tabelul de date este redat pe 3 pagini şi pe fiecare, începe cu un titlu de tabel aliniat la stânga (numele şcolii), urmat de un "cap de tabel". În prima coloană avem numele claselor (cu mărime de font foarte mare); celelalte 35 de coloane sunt dimensionate după lăţimea de pagină (implicând după caz, despărţirea cuvântului înscris în celulă) şi conţin obiectele fiecărei clase, pe zile şi ore.
Primul lucru la care merită să te uiţi este "Document Properties", unde găsim Producer: Microsoft: Print To PDF; deci orar.pdf provine dintr-un fişier Excel (cum şi era de aşteptat, văzând tabelul din care am redat mai sus), anume (luându-ne după semnătura din subsolul documentului) cel furnizat de "aSc Orare".
În treacăt fie spus, nu s-a făcut niciun „efort” (creativ) de a specula puţin fişierul Excel iniţial, pentru a prezenta orarul clasei într-o formă normală – de exemplu astfel:
12C 1 2 3 4 5 6 7 Lu Info-apl Info-apl Info-apl Info-Lab Info-Lab Rel.ort EdF Ma Mate Mate Rom Fiz Ist - Mi Mate Rom Fiz Eng Germ - Jo Rom Chim Mate Info-teo Info-teo Eng - Vi Fiz Mate Bio Filos Dir Germ Geo
Excel-ul fiind privit ca instrument de formatare, toate eforturile s-au îndreptat în această direcţie (aranjează „antete” de pagini, setează dimensiuni pentru celule, bordere, fonturi, etc.).
Fiindcă ne interesează datele conţinute – transformăm cumva înapoi, apelând de exemplu la serviciile de conversie oferite gratuit de Adobe: prin formularul din www.adobe.com/acrobat/online/pdf-to-excel.html obţinem „înapoi” fişierul orar.xlsx.
Prima problemă care apare ţine de antet; într-un tabel Excel nu avem un antet propriu-zis (cum putem defini într-un tabel HTML, de exemplu), ci doar un „antet de pagină” – compus aici din titlul documentului şi un „cap de tabel”, repetat la începutul fiecărei pagini (de fapt, doar în fişierul PDF apare astfel).
Fiindcă nu ne interesează să tipărim documentul respectiv (nici să-l admirăm pe ecran) – să îndrăznim să eliminăm antetul (folosind mouse-ul şi meniurile din Gnumeric) – dar pentru prudenţă, salvăm rezultatul într-un fişier nou, orar2.xlsx (antetul este conexat cu regiunile de linii şi coloane care definesc fiecare pagină în parte, încât a-l „elimina” – dacă se poate – este oarecum riscant, putând duce la „pierderea” unei coloane, de exemplu).
A doua problemă constă în extragerea datelor din celulele tabelului Excel, într-o anumită „structură internă de date”. Cel mai simplu procedeu ar fi acesta: transformăm în format CSV, folosind programul utilitar ssconvert (asociat lui Gnumeric) – apoi, fişierul CSV rezultat poate fi integrat imediat ca structură de date, de exemplu în R (invocând read.csv()). Dar în cazul de faţă, acest procedeu este defectuos, fiindcă avem şi celule colapsate ("merged cells"):

La transformarea în format CSV a fişierului, obţinem (greşit):
12A,Info-apl,,,Info-Lab,,,,,Rom,,
reflectând numai prima dintre celulele colapsate (trei, sau două) pe care apare "Info-apl", "Info-lab", respectiv "Rom". Corect era ca "Info-apl" să fi fost repetat de trei ori, "Info-lab" de două ori, etc.; dar ssconvert (sau meniul care-i corespunde în Gnumeric) omite cazul celulelor colapsate pe orizontală.
Zicem noi, "corect era…"; dar de fapt comportamentul lui ssconvert este firesc: numai ca aspect vizual (în urma aplicării pe un grup de celule a formatării "Merge"), acel "Info-apl" apare pe trei celule – în realitate numai prima celulă dintre cele trei, conţine "Info-apl" (celelalte rămân goale).
În pachetul R openxlsx avem o funcţie care prevede un parametru prin care se poate forţa tratarea dorită mai sus pentru celulele colapsate:
> GM2 <- openxlsx::read.xlsx("orar2.xlsx", sheet=1, colNames=FALSE, fillMergedCells = TRUE) > tail(GM2[, 1:6]) X1 X2 X3 X4 X5 X6 55 Info-apl Info-apl Info-apl Info-Lab Info-Lab EdF 56 Info-apl Info-apl Info-apl Info-Lab Info-Lab EdF 57 Mate Mate Rom Fiz Geo Info-te o 58 Mate Mate Rom Fiz Geo Info-te o 59 EdF Franc Mate Mate Fiz Eng 60 EdF Franc Mate Mate Fiz Eng
Constatăm că "Info-apl" a fost repetat pe trei coloane, etc. – cum doream.
Fiindcă în orar2.xlsx nu mai avem "antet", coloanele au fost denumite generic 'X1', 'X2', 'X3' ş.a.m.d.; însă… constatăm că prima coloană din fişierul Excel – cea pe care figurau numele claselor – a fost omisă!
Singura explicaţie de luat în seamă vine de la faptul că fişierul orar2.xlsx a rezultat sub Gnumeric (care este doar compatibil, cu Excel), prin „eliminarea” antetului existent în orar.xlsx… Să revedem deci, antetul respectiv:
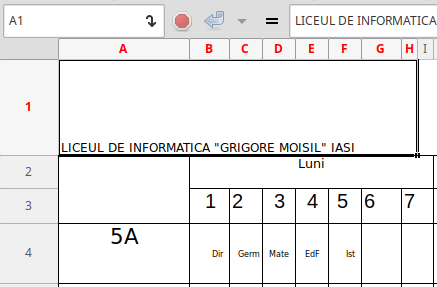
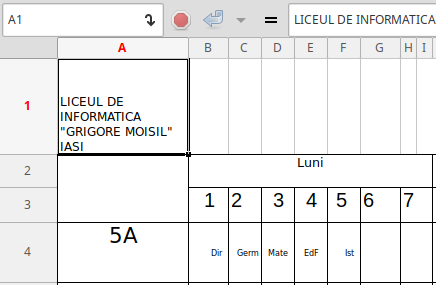
Prima dintre cele două porţiuni de pe rândul 1 ale antetului, ocupă zona 'A'..'H' – dar de fapt, ocupă efectiv celula 'A1' (cum este notat în boxa din stânga-sus şi cum se vede şi mai clar pe a doua imagine – rezultată prin meniul "Cell / Unmerge"); coloana 'A' (cu numele claselor) o fi „dispărut” fiindcă am eliminat (probabil, incomplet) antetul…
Folosind "Unmerge" pentru a doua porţiune de pe rândul 1, constatăm că titlul respectiv ocupă efectiv celula 'I1' (extinzându-se spre dreapta); coloana 'I' este de fapt goală, fiind colapsată coloanei 'H'.
Ducând orar2.xlsx în Google Spreadsheet, am observat că se poate elimina uşor coloana 'I' (nu ştiu cum de n-am reuşit s-o selectez, din Gnumeric); salvând după aceasta înapoi în orar2.xlsx şi reluând apoi read.xlsx() ca mai sus – am obţinut în GM2 toate coloanele şi acum avem şi numele claselor (sau NA), în prima coloană:
> tail(GM2[, 1:8]) X1 X2 X3 X4 X5 X6 X7 X8 55 12D Info-apl Info-apl Info-apl Info-Lab Info-Lab EdF <NA> 56 <NA> Info-apl Info-apl Info-apl Info-Lab Info-Lab EdF <NA> 57 12E Mate Mate Rom Fiz Geo Info-te o Franc 58 <NA> Mate Mate Rom Fiz Geo Info-te o Franc 59 12F EdF Franc Mate Mate Fiz Eng Filos 60 <NA> EdF Franc Mate Mate Fiz Eng Filos
Avem acum cum voiam, un „set de date” de tip data.frame, conţinând datele din fişierul PDF de la care am plecat – în fond, un „tabel” intern referit prin GM2, cu 60 de linii pe 36 de coloane, conţinând valori de tip chr; valorile care lipsesc (aferente celulelor goale din Excel) sunt reprezentate prin constanta logică NA.
Salvăm rezultatul, pentru a-l recupera uşor în vreo nouă sesiune de lucru:
> saveRDS(GM2, file = "GM2.rds")
Îndreptări
Scopul nostru este de a formula o încadrare posibilă a presupuşilor profesori, care să corespundă orarului pe obiecte înregistrat în GM2; dar mai întâi se cuvine să facem o serie de modificări: cea mai simplă constă în mici reparaţii sintactice (trebuie "Info-teo" şi nu "Info-te o", cum apăruse în Excel în urma redimensionării celulelor coloanei); apoi, tot simplu, să schimbăm numele generice 'X1', 'X2' etc. cu denumiri potrivite; apoi (poate ceva mai complicat), să corectăm un anumit neajuns produs la expandarea celulelor colapsate vertical (a vedea mai sus, liniile ca 57 şi 58, corespunzătoare unei aceleiaşi clase); în sfârşit şi cel mai important – să „normalizăm” structura datelor.
Iniţiem un program prin care să modelăm aceste modificări preliminare:
# prelim.R library(tidyverse) GM2 <- readRDS("GM2.rds")
Setarea numelor de coloană
Desemnăm prima coloană (cu numele claselor, sau NA ca valori) prin 'cls', iar celelalte coloane prin combinaţii între numele zilelor (abreviate) şi indecşii 1..7 ai orelor:
zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") antet <- paste0(zile, rep(1:7, 5)) %>% sort() antet <- c('cls', antet[8:28], antet[1:7], antet[29:35]) colnames(GM2) <- antet # cls Lu1 Lu2 ... Lu7 Ma1 ... Ma7 ... Vi1 ... Vi7
Notaţia introdusă (care imită în fond, capul de tabel din fişierul PDF iniţial) are însă acest defect: într-un acelaşi nume am implicat două variabile independente – o "zi" şi o "oră" (semn că structura de date respectivă nu este în „forma normală”).
Reglarea liniilor aferente unei aceleiaşi clase
În "Orarul general clase" apar grupuri de celule colapsate orizontal sau/şi vertical:

Colapsarea orizontală exprimă faptul că obiectul respectiv este alocat pe mai multe ore consecutive; read.xlsx() (cu opţiunea fillMergedCells) a interpretat corect (spre deosebire de ssconvert), repetând obiectul pe coloane consecutive.
Colapsarea verticală exprimă faptul că ora sau orele respective se desfăşoară „pe grupe”: clasa este despărţită în două grupe, fiecăreia fiindu-i alocat câte un profesor (şi câte o anumită sală de clasă/laborator). De exemplu (v. imaginea redată mai sus), în zilele luni şi marţi, 9B este despărţită în câte două grupe pentru primele 3 ore (de "Info-apl") şi respectiv, în ora a 6-a (când o grupă are "Muz", iar cealaltă are "Des").
read.xlsx() interpretează cam simplist, colapsarea verticală: pur şi simplu dublează linia clasei – copiind pe o nouă linie toate datele acesteia exceptând numele clasei (înlocuit cu NA); în schimb, ssconvert procedează corect, înscriind pe o nouă linie CSV, în locul cuvenit, numai obiectul colapsat (neglijând însă, eventuala colapsare şi pe orizontală, a acestuia).
Cum putem constata răsfoind orar.pdf, colapsarea verticală vizează numai Info-apl, Muz şi Des; pentru a corecta interpretarea dată de read.xlsx(), n-avem decât să înlocuim prin NA toate celelalte obiecte, pe toate liniile care au NA în câmpul $cls:
twins <- c("Info-apl", "Des", "Muz") # din celulele colapsate vertical for(i in 1:nrow(GM2)) { K <- GM2[i, ] if(is.na(K[1])) { # linie cu 'NA' în câmpul "cls" K[! K %in% twins] <- NA GM2[i, ] <- K } }
Dar oare nu puteam proceda mai inteligent? De ce să păstrăm o linie doar pentru a indica faptul că o anumită oră este partajată la clasa respectivă de către doi profesori (fiecare la câte o grupă)?
Dacă am fi siguri că "Info-apl" este la oricare clasă la care apare, în sarcina aceloraşi doi profesori, iar "Muz" şi "Des" se fac numai „pe grupe” – atunci da, am putea proceda mai inteligent: am şterge toate liniile care aveau NA în câmpul $cls.
Însă în orar.pdf, apare "Info-apl" şi într-un acelaşi timp (zi şi interval orar), la mai multe clase – însemnând că există mai multe cupluri de profesori pe obiectul respectiv (în ziua respectivă, fiecare cuplu intră la câte una dintre clase); în plus, există clase care fac separat "Des" şi respectiv, "Muz".
Totuşi… ştiind care clase fac separat "Des" şi "Muz" (şi mai ştiind că "Info-apl" se face numai „pe grupe”), am putea reconstitui cuplajele şi fără liniile cu NA în coloana $cls!
Consultând mai atent orar.pdf, constatăm că într-adevăr "Info-apl" se face numai „pe grupe” şi că numai clasele „mici” 5-8, fac separat "Des" şi "Muz" – prin urmare, putem elimina toate liniile cu NA în coloana $cls:
GM <- GM2 %>% filter(! is.na(cls)) saveRDS(GM, file = "GM.rds")
În "GM.rds" avem un număr de linii egal cu numărul de clase (şi 36 de coloane).
Când vom vedea "Des" sau "Muz" la o clasă a 9-a sau a 10-a – vom şti că ora respectivă este partajată pe câte o grupă de elevi, de cei doi profesori; când vom vedea "Info-apl", vom şti că ora respectivă este partajată de doi profesori (care desigur, nu pot partaja într-un interval orar dat, decât o singură clasă).
Normalizarea structurii datelor
> print(GM[1, 1:18], width=100) cls Lu1 Lu2 Lu3 Lu4 Lu5 Lu6 Lu7 Ma1 Ma2 Ma3 Ma4 Ma5 Ma6 Ma7 Mi1 Mi2 Mi3 5A Dir Germ Mate EdF Ist <NA> <NA> Mate Bio Rom Geo Des Ist <NA> Rel.ort\n. EdT Mate
Am afişat jumătate din prima linie, pentru a ilustra structura curentă a datelor din GM; în coloana $cls avem numele clasei, 5A, iar în coloanele următoare avem obiectele repartizate clasei, pe zile şi ore (sau eventual NA – „oră liberă”).
Putem afla imediat care sunt clasele: acestea apar într-o singură coloană şi obţinem vectorul care le conţine prin GM$cls (sau folosind indexarea, prin GM[, 1]). În schimb, ca să aflăm care sunt obiectele – avem de căutat în coloanele 2:36, reţinând pe parcurs obiectele întâlnite pentru prima dată (dacă obiectele ar fi stat într-o singură coloană, ca în cazul claselor, atunci răspunsul era iarăşi, imediat).
Pentru facilitarea investigării sau prelucrării datelor, acestea trebuie structurate astfel încât fiecare valoare să aparţină unei singure variabile (sau unui singur câmp, sau domeniu de valori), iar variabilele considerate să fie independente între ele.
Variabilele care definesc valorile din orarul GM sunt: clasa, obiectul, ziua şi ora – şi acestea sunt independente, având fiecare propriul domeniu de valori. Dar numai "clasa" este explicitată, în coloana $cls; valorile de "obiect" sunt răsfirate pe toate celelalte coloane, iar "zi" şi "oră" sunt amestecate chiar în numele coloanelor.
Putem normaliza (sau „igieniza”) datele, îmbinând funcţii din pachetul tidyr (inclus în „dialectul” tidyverse):
GM <- GM %>% pivot_longer(cols = 2:36, names_to = "zi_ora", values_to = "obj", values_drop_na = TRUE) %>% # fără NA separate(col = "zi_ora", into = c("zi", "ora"), sep = 2, convert = TRUE) # "ora" capătă valori 'int'
pivot_longer() a luat toate valorile din coloanele 2:36 (exceptând NA) şi le-a depus în coloana denumită "obj", corespunzător valorilor din coloana "zi_ora" – înfiinţată pentru a înregistra numele de coloană iniţiale "Lu1", "Lu2", ..., "Vi7".
Apoi, separate() a separat după primele două caractere valorile existente în coloana "zi_ora", înfiinţând coloanele "zi" (cu valori de tip chr) şi "ora" (cu valori de tip int):
> str(GM) tibble [1105 × 4] (S3: tbl_df/tbl/data.frame) $ cls: chr [1:1105] "5A" "5A" "5A" "5A" ... $ zi : chr [1:1105] "Lu" "Lu" "Lu" "Lu" ... $ ora: int [1:1105] 1 2 3 4 5 1 2 3 4 5 ... $ obj: chr [1:1105] "Dir" "Germ" "Mate" "EdF" ...
Având această formă pentru GM, vom putea răspunde uşor (folosind tidyverse) la orice chestiune asupra datelor respective.
Deocamdată, vedem că în şcoala respectivă se desfăşoară exact 1105 ore (lecţii) pe săptămână: fiecare lecţie implică o anumită clasă, o anumită zi, o oră a zilei şi un obiect – deci echivalează cu o linie din „tabelul” (obiect de memorie de tip tibble) GM. Norma uzuală fiind de 18 ore, urmează că avem în jur de 60 de profesori.
Factorizări
Să vedem care sunt obiectele de studiu prevăzute (prin abreviere) în orar:
> unique(GM$obj) %>% sort() [1] "Algor" "Antre" "Bio" "Chim" "Des" [6] "Dir" "Econ" "Ed. soc" "EdF" "EdT" [11] "Eng" "Filos" "Fiz" "Franc" "Geo" [16] "Germ" "Info" "Info-apl" "Info-L ab" "Info-La b" [21] "Info-Lab" "Info-te o" "Ist" "Lat" "Log" [26] "Mat opt" "Mate" "Muz" "Psih" "Rel.ort\n." [31] "Rom" "Rom opt" "TIC"
Să zicem că ar fi de simplificat unele denumiri: de exemplu, am vrea EdSoc în loc de "Ed. soc" şi infApl în loc de "Info-apl"; deasemenea, infLab în loc de "Info-L ab" şi Rel în loc de "Rel.ort\n.", ba chiar şi Mat în loc de "Mate", etc.
Dar să observăm întâi că (rezultat obişnuit al ajustării manuale a celulelor, pe fişierul Excel iniţial) avem trei denumiri distincte "Info-L ab", "Info-La b" şi "Info-Lab" pentru – cu siguranţă – un acelaşi obiect. Trebuie să unificăm cumva, aceste denumiri:
> GM$obj[GM$obj %in% c("Info-L ab", "Info-La b", "Info-Lab")] <- "infLab"
În general, fiecare obiect apare pe mai multe linii din GM – dar în loc să modificăm pe fiecare dintre aceste linii, putem proceda mai simplu: transformăm $obj în factor,
> GM$obj <- factor(GM$obj) > str(GM$obj) Factor w/ 31 levels "Algor","Antre",..: 6 16 25 9 21 25 3 29 15 5 ...
Cele 31 de nume de obiecte sunt păstrate într-un vector care poate fi accesat prin funcţia levels(), iar în GM$obj se înscriu indecşii numerici ai acestora (în loc de numele respective). Acum, pentru a schimba cum dorim denumirile obiectelor, n-avem decât să modificăm vectorul dat de levels() (dar atenţie: trebuie păstrată ordinea iniţială a nivelelor – deci întâi le afişăm prin cat('"', levels(GM$obj), sep='", "', '"'), le copiem într-un editor de text, le modificăm şi în final ambalăm totul într-un c(...)):
levels(GM$obj) <- c("Algor", "Antre", "Bio", "Chi", "Des", "Dir", "Econ", "edSoc", "edFiz", "edTeh", "Eng", "Filos", "Fiz", "Fra", "Geo", "Ger", "infLab", "Inf", "infApl", "infTeo", "Ist", "Lat", "Log", "matOpt", "Mat", "Muz", "Psih", "Rel", "Rom", "romOpt", "TIC")
Fiindcă $obj este factor (altfel, table() ar fi transformat ea însăşi, în factor), avem imediat şi o situaţie după numărul total de ore, pe obiecte:
> sort(table(GM$obj), decreasing = TRUE) Mat Rom Fiz Eng infApl Bio edFiz Chi infTeo Ist Geo 160 127 90 72 72 55 54 48 42 42 39 Dir Fra Ger Rel TIC Des infLab Muz edSoc edTeh Algor 36 36 36 36 30 18 18 18 12 12 9 Inf Antre Econ Filos Log Psih Lat matOpt romOpt 7 6 6 6 6 6 3 2 1
Împărţind la norma standard de 18 ore, putem estima cam câţi profesori sunt încadraţi pe câte un acelaşi obiect: 8-9 profesori fac Mat, etc.; cele 72 de ore infApl se fac numai „pe grupe”, deci există 4 cupluri de profesori care fac infApl.
Desigur, pentru unele obiecte va trebui să ţinem seama de un anumit context subînţeles; de exemplu, Dir are 36 de ore – dar aceasta nu înseamnă că ar fi doi profesori (36/18) încadraţi pe acest obiect: subînţelegem că este vorba de "Dirigenţie", care se face pe câte o oră la fiecare clasă, de către unul dintre profesorii acelei clase (şi… deja ne dăm seama că nu vom putea depista cine face Dir).
Încadrarea obiectelor pe clase
Probabil că vom putea deduce mai multe informaţii privind încadrarea profesorilor, dacă am evidenţia numărul de ore pe fiecare clasă şi obiect:
frm <- addmargins(table(GM[c("obj", "cls")]))
Însă print(frm, ...) consumă prea mult spaţiu, faţă de cât ar fi necesar; să folosim mai bine cat() pentru a produce cu un format potrivit, fiecare linie din frm.
Constituim întâi un „antet” care să consume cât mai puţin spaţiu orizontal; notăm nivelele de clase câte o singură dată (de exemplu, "10__________") şi dedesubt scriem literele claselor de pe nivelul respectiv (în exemplu, " A B C D E F")
(referindu-ne la structură şi nu la scriere – desemnăm coloanele lui frm prin literele claselor, făcând o excepţie de la regula unicităţii numelor de coloană):
CLS <- sort(unique(GM$cls)) # numele claselor, în ordine lexicografică lCLS <- str_extract(CLS, "[A-Z]") # şirul literelor claselor colnames(frm) <- c(lCLS, "+") # "+" pentru coloana frm$Sum frm[frm == 0] <- '.' # implicit, întregii devin "chr" separ <- function(v, n) paste0(v, sep = paste0(rep("_", n), collapse=""), collapse="") ant1 <- separ(10:12, 10) # "10__________11__________12__________" ant2 <- separ(paste0(" ", 5:8), 4) # " 5____ 6____ 7____ 8____" ant3 <- separ(" 9", 10) # " 9__________" indent <- " " ant <- paste0(indent, ant1, ant2, ant3, collapse="") # antetul tabelului
Următoarea secvenţă scrie (prin cat()) în fişierul indicat funcţiei sink(), întâi antetul constituit mai sus, apoi liniile din frm şi în final, iarăşi antetul:
sink("frm_obj.txt") cat(ant, "\n") cat(indent, colnames(frm), "\n") nr <- nrow(frm) for(i in 1:(nr-1)) { nume <- sprintf("%6s", rownames(frm)[i]) cat(nume, frm[i, ], "\n") } cat(" ", colnames(frm), "\n") cat(ant, "\n") cat("Total ") for(i in seq(1, ncol(frm), 2)) cat(frm[nr, i], " ") cat("\n ") for(i in seq(2, ncol(frm), 2)) cat(" ", frm[nr, i]) sink()
Fişierul rezultat (care poate fi redat pe o singură coală "A4") este important şi în sine, sintetizând informaţiile privitoare la obiecte şi clase; între altele, avem şi totalurile de ore pe obiecte şi pe clase (determinate iniţial de addmargins()):
# încadrarea obiectelor pe clase 10__________11__________12__________ 5____ 6____ 7____ 8____ 9__________ A B C D E F A B C D E F A B C D E F A B C A B C A B C A B C A B C D E F + Algor . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 . . . . . . . . . 9 Antre 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Bio 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 2 2 2 2 2 1 1 1 2 2 2 2 2 2 55 Chi 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 2 2 2 2 2 2 2 2 2 2 2 2 48 Des 1 1 1 1 1 1 . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 18 Dir 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 36 Econ . . . . . . 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . 6 edSoc . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 12 edFiz 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 54 edTeh . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 12 Eng 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 72 Filos . . . . . . . . . . . . 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . 6 Fiz 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 . . . 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 90 Fra . 2 2 2 . . . . 2 2 2 2 . . . 2 2 2 . . 2 2 . 2 2 . . . 2 . 2 2 . . . 2 36 Geo 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 1 1 1 1 39 Ger 2 . . . 2 2 2 2 . . . . 2 2 2 . . . 2 2 . . 2 . . 2 2 2 . 2 . . 2 2 2 . 36 infLab . . . . . . 1 1 1 1 1 1 2 2 2 2 2 2 . . . . . . . . . . . . . . . . . . 18 Inf . . . . . . . . . . . . . . . . . . 1 1 . 1 1 1 1 . . . 1 . . . . . . . 7 infApl 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 . . . . . . . . . . . . 3 3 3 3 3 3 72 infTeo 1 1 1 1 1 1 3 3 3 3 3 3 2 2 2 2 2 2 . . . . . . . . . . . . 1 1 1 1 1 1 42 Ist 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 1 1 42 Lat . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 . . . . . . . . . 3 Log . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 6 matOpt . . . . . . . . . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . 2 Mat 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 4 4 5 4 5 4 4 4 4 5 5 4 5 5 4 4 4 4 4 4 160 Muz . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 18 Psih 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Rel 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 36 Rom 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 5 4 4 4 4 4 4 4 4 127 romOpt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . 1 TIC 1 1 1 1 1 1 . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 30 A B C D E F A B C D E F A B C D E F A B C A B C A B C A B C A B C D E F + 10__________11__________12__________ 5____ 6____ 7____ 8____ 9__________ Total 32 32 32 30 30 30 30 30 30 28 27 29 32 32 32 32 32 32 1105 32 32 32 30 30 30 30 30 30 27 29 29 32 32 32 32 32 32
La sfârşit, am redat pe două linii, alternativ, totalurile de ore pe coloane (pe clase); astfel, putem distinge că 10A are 32 de ore, iar clasa imediat următoare 10B are 32 de ore ș.a.m.d. (dacă le-am fi redat pe o singură linie, trebuia să le separăm prin spațiu și atunci, liniile se lărgeau prea mult).
Marcarea profesorilor
Pe fiecare obiect – din levels(GM$obj) – avem câte unul sau mai mulţi profesori; constituim numele de profesori abreviind la câte două litere, numele de obiecte (şi ulterior, pentru a distinge între profesorii pe un acelaşi obiect, vom adăuga numelui de două litere câte o cifră):
Prof <- abbreviate(levels(GM$obj), minlength=2, strict=TRUE) Algor Antre Bio Chi Des Dir Econ edSoc edFiz edTeh Eng "Al" "An" "Bi" "Ch" "Ds" "Dr" "Ec" "eS" "eF" "eT" "En" Filos Fiz Fra Geo Ger infLab Inf infApl infTeo Ist Lat "Fl" "Fz" "Fr" "Ge" "Gr" "iL" "In" "iA" "iT" "Is" "Lt" Log matOpt Mat Muz Psih Rel Rom romOpt TIC "Lg" "mO" "Mt" "Mz" "Ps" "Rl" "Rm" "rO" "TI"
De exemplu, profesorii care fac "infApl" au numele de bază dat de Prof[["infApl"]], anume "iA" şi dacă vom deduce că sunt în număr de 4 – îi vom numi "iA1", "iA2", "iA3" şi "iA4" (urmând să vedem la care clase au ore, fiecare).
Desigur, la un anumit moment va trebui să ţinem seama de faptul că un profesor pe un anumit obiect este acelaşi cu un profesor pe un alt obiect; de exemplu, dirigintele "Dr5" al unei clase este unul dintre profesorii pe un anumit obiect (propriu-zis) al acelei clase; la fel de exemplu, "rO2" care face "Română-Opţional" la o clasă este cel mai probabil, profesorul "Rm2" care face "Română" la acea clasă.
Deasemenea, când vom vedea că un profesor are un număr mic de ore – vom identifica profesorul respectiv cu unul de o aceeaşi specialitate care are mai multe ore (urmărind însă ca „norma” acestuia să nu depăşească mult, norma uzuală de 18 ore).
De exemplu, din încadrarea pe obiecte redată mai sus, vedem că pe obiectul "Inf" sunt numai 7 ore pe săptămână; este atunci firesc să considerăm că profesorul prof[["Inf"]] este de fapt, unul (sau poate mai mulţi) dintre profesorii de aceeaşi specialitate (cel mai probabil, "Informatică" – deci "iL", "iA", "iT", sau poate "TIC").
Construcţia unei încadrări pe clase a profesorilor
Contextul şcolar obişnuit sugerează o simplificare: "dirigenţia" este o oră la fiecare clasă şi este atribuită unuia sau altuia dintre profesorii clasei, independent de specialitate şi de norma orară (fiind plătită separat).
Aşa că ni se pare firesc să eliminăm "Dir", urmând să vizăm încadrarea profesorilor pe obiectele de învăţământ propriu-zise:
GM <- GM %>% filter(obj != "Dir") %>% # exclude dirigenţiile (obiectul "Dir") droplevels() # elimină nivelul "Dir" al factorului "obj" Prof <- Prof[-6] # elimină "Dr" (profesor diriginte, al 6-lea în vectorul 'prof')
Ideea pe care mizăm pentru a produce o încadrare (plauzibilă) pe clase a profesorilor este următoarea: considerăm pe rând câte un set de lecţii care sunt alocate într-o aceeaşi zi şi oră (5 zile × 7 ore = 35 de seturi); dacă într-un asemenea set, "Mat" de exemplu, apare de 4 ori – atunci înfiinţăm 4 profesori "Mt1", "Mt2", etc. şi îi atribuim claselor respective. În final, pe fiecare set vom avea câte o coloană "prof" conţinând profesorii înfiinţaţi şi ne rămâne să sintetizăm – stabilind pentru fiecare profesor, vectorul claselor la care are ore (rămâne apoi, să ajustăm încadrarea obţinută).
Concret, procedăm desigur mai simplu decât am enunţat mai sus: înfiinţăm de la bun început coloana $prof, înscriindu-i ca valori iniţiale numele de bază din vectorul Prof (corespunzător obiectelor înregistrate în coloana $obj); constituim o listă 'izo' conţinând cele 35 de seturi de lecţii pe câte o aceeaşi zi şi oră:
izo <- GM %>% mutate(prof = Prof[obj]) %>% # înfiinţăm coloana 'prof' split(list(.$zi, .$ora)) # seturi de lecţii pe aceeaşi zi şi oră
Exemplificăm ce avem de făcut, pe unul oarecare dintre cele 35 de seturi:
> izo[[1]] %>% arrange(obj) # A tibble: 36 x 5 cls zi ora obj prof <chr> <chr> <int> <fct> <chr> 1 6B Jo 1 Bio Bi # Bi1 (Prof[["Bio"]] este "Bi") 2 10F Jo 1 Bio Bi # Bi2 3 12E Jo 1 Bio Bi # Bi3 4 9D Jo 1 Chi Ch # Ch1 (Prof[["Chi"]] este "Ch") 5 9E Jo 1 Chi Ch # Ch2 6 12F Jo 1 Chi Ch # Ch3 7 9B Jo 1 edFiz eF # eF1 8 5B Jo 1 Eng En 9 7A Jo 1 Eng En 10 11C Jo 1 Eng En # … with 26 more rows
Jo ora 1 se fac 3 ore de "Bio" (cu profesori distincţi); în vectorul Prof, pe "Bio" avem "Bi" – deci în coloana $prof avem de înscris "Bi1", "Bi2" şi "Bi3" (adică de adăugat o cifră, numelor "Bi" înscrise din start). Procedăm analog pentru toate celelalte obiecte (şi la fel, pentru toate cele 35 de seturi).
Pentru a proceda unitar – rămânând eventual, să ajustăm ulterior – convenim să adăugăm totdeauna o cifră (începând cu "1", până epuizăm numărul de ore pe obiectul curent, în ziua respectivă) numelui de bază înscris iniţial în coloana $prof (chiar şi când apare o singură oră, cum avem mai sus pentru "edFiz").
Dar subliniem că acest procedeu „unitar” este cam simplist: fiindcă pe fiecare dintre cele 35 de seturi indexăm profesorii pe acelaşi obiect de la 1, rezultă că "..1" (de exemplu, "Mt1") va avea totdeauna, cel mai multe clase (urmat de "..2", etc.) şi vom avea de făcut anumite ajustări, dacă vrem să echilibrăm numărul de ore pentru profesorii de pe un acelaşi obiect.
Desigur, iarăşi vom proceda mai inteligent decât am exemplificat mai sus: întâi grupăm liniile din GM după $zi, $ora şi $prof; de exemplu, grupul pentru ziua Jo, ora 1 şi profesorul "Bi" va conţine exact liniile 1, 2 şi 3 marcate în exemplificarea de mai sus.
Dacă am adăuga imediat câte o cifră cum am arătat mai sus, atunci la unele obiecte va apărea situaţia că sunt doi profesori la aceeaşi clasă: de exemplu, să zicem că în prima zi apare "Mat" la clasa "6B" o singură dată şi într-o altă oră decât celelalte clase cu "Mat" – atunci în coloana "$prof", la "6B" ar fi înscris "Mt1"; dacă în următoarea zi, ar apărea "6B" cu "Mat" în orele 1, 2 şi 3 şi deasemenea, o altă clasă cu "Mat" în ora 1 – atunci la "6B" va trebui alocat (probabil) şi "Mt2" (încât la "6B" unele ore de "Mat" vor fi la "Mt1", altele la "Mt2").
Pentru a evita o asemenea situaţie, nu vom ađauga imediat indecşii de profesor – ci îi vom înscrie într-o coloană temporară "$idp"; apoi, vom proceda astfel: considerăm pe rând, câte un set de lecţii pe un acelaşi obiect, îl grupăm pe clase şi pentru fiecare grup, alipim în câmpul $prof cel mai mare index din coloana $idp (astfel, în exemplul cu "6B" de mai sus, vom avea deodată "Mt2" pe toate orele de "Mat").
Secvenţa de program necesară este scurtă şi elegantă (spre deosebire de „povestea” ei, exemplificată căznit mai sus), speculând faptul că după ce grupăm, mutate() acţionează pe fiecare grup în parte:
GMP <- GM %>% mutate(prof = Prof[obj]) %>% group_by(zi, ora, prof) %>% mutate(idp = 1:n()) %>% # n() dă numărul de linii din grupul curent ungroup() spo <- GMP %>% split(.$obj) for(i in 1:length(spo)) spo[[i]] <- spo[[i]] %>% group_by(cls) %>% mutate(prof = paste0(prof, max(idp))) %>% ungroup() GMP <- do.call("rbind", spo) GMP$idp <- NULL
În final, am reunit prin rbind() seturile din lista spo – refăcând setul întreg GMP, dar acum cu valori corecte în coloana $prof; pentru exemplificare,
> slice_sample(GMP, n = 5) # A tibble: 5 x 5 cls zi ora obj prof 1 11D Ma 5 Mat Mt7 2 5C Jo 4 Mat Mt1 3 11B Lu 1 Rom Rm4 4 7B Ma 7 edFiz eF1 5 12F Jo 7 Ist Is2
Cu aceeaşi secvenţă de program cu care am produs anterior „încadrarea obiectelor pe clase”, putem obţine acum din GMP, încadrarea brută a profesorilor pe clase:
# încadrarea profesorilor (brută) 10__________11__________12__________ 5____ 6____ 7____ 8____ 9__________ A B C D E F A B C D E F A B C D E F A B C A B C A B C A B C A B C D E F + Al1 . . . . . . . . . . . . . . . . . . 1 1 . 1 1 1 1 1 1 . . . . . . . . . 8 Al2 . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . 1 An1 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Bi1 . 2 . . . . . . . . . 1 . . . . . . 1 1 1 2 2 2 2 . 2 1 . 1 2 2 2 . . . 24 Bi2 2 . . . 2 2 1 1 1 1 1 . 1 . 1 . . 1 . . . . . . . 2 . . 1 . . . . 2 2 2 23 Bi3 . . 2 2 . . . . . . . . . 1 . . 2 . . . . . . . . . . . . . . . . . . . 7 Bi4 . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . . . . . 1 Ch1 . . . 2 . . . . . 1 1 1 . . . . . . . . . . . . 2 2 2 . 2 2 . 2 . 2 . 2 21 Ch2 . 2 2 . 2 2 1 1 1 . . . 1 . . . 1 . . . . . . . . . . 2 . . 2 . 2 . 2 . 21 Ch3 2 . . . . . . . . . . . . 1 1 1 . 1 . . . . . . . . . . . . . . . . . . 6 Ds1 1 1 1 1 1 1 . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 18 Ec1 . . . . . . 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . 6 eF1 . . . 2 2 2 1 . . . 1 . 1 . 1 . . . 2 2 2 2 . 2 2 2 2 2 . . . 1 1 . 1 . 31 eF2 2 2 2 . . . . 1 1 1 . 1 . 1 . 1 1 1 . . . . 2 . . . . . 2 2 1 . . 1 . 1 23 En1 . . . . . . . . . . . . . . . . . . 2 2 2 2 2 2 . . 2 2 . . . . . . 2 . 18 En2 2 . 2 2 2 2 2 . . . 2 . . . . . . . . . . . . . 2 2 . . 2 . 2 . 2 . . 2 26 En3 . 2 . . . . . 2 2 2 . . . . 2 . . 2 . . . . . . . . . . . 2 . 2 . 2 . . 18 En4 . . . . . . . . . . . 2 2 2 . 2 2 . . . . . . . . . . . . . . . . . . . 10 eS1 . . . . . . . . . . . . . . . . . . 1 1 1 1 1 . 1 . 1 1 1 1 . . . . . . 10 eS2 . . . . . . . . . . . . . . . . . . . . . . . 1 . 1 . . . . . . . . . . 2 eT1 . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 . . . . . . 12 Fl1 . . . . . . . . . . . . 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . 6 Fr1 . 2 2 2 . . . . 2 . . . . . . . 2 . . . 2 2 . 2 2 . . . 2 . 2 . . . . . 22 Fr2 . . . . . . . . . 2 2 2 . . . 2 . 2 . . . . . . . . . . . . . 2 . . . 2 14 Fz1 . . . . . . . . . . . . . . . . . . . . . 2 2 2 2 . 2 2 . 2 3 . . . . . 17 Fz2 3 3 . . . . . . . . . . . . . . . . . . . . . . . 2 . . . . . 3 3 . . 3 17 Fz3 . . 3 3 3 3 . 3 . . 3 3 3 3 3 . 3 3 . . . . . . . . . . 2 . . . . 3 3 . 44 Fz4 . . . . . . 3 . 3 3 . . . . . 3 . . . . . . . . . . . . . . . . . . . . 12 Ge1 . 1 1 1 1 . 1 . . 1 1 1 . . 1 . 1 . 1 1 1 1 1 1 1 1 1 2 . 2 1 . 1 1 1 1 28 Ge2 1 . . . . 1 . 1 1 . . . 1 1 . 1 . 1 . . . . . . . . . . 2 . . 1 . . . . 11 Gr1 . . . . 2 . 2 . . . . . . . 2 . . . 2 2 . . 2 . . 2 2 2 . 2 . . . . . . 20 Gr2 2 . . . . 2 . 2 . . . . 2 2 . . . . . . . . . . . . . . . . . . 2 2 2 . 16 iA1 . 3 3 3 . . . . . 3 . . . . . . . . . . . . . . . . . . . . 3 3 . 3 3 . 24 iA2 . . . . . 3 3 . 3 . 3 . 3 . . . 3 . . . . . . . . . . . . . . . 3 . . 3 24 iA3 3 . . . . . . 3 . . . 3 . 3 3 . . 3 . . . . . . . . . . . . . . . . . . 18 iA4 . . . . 3 . . . . . . . . . . 3 . . . . . . . . . . . . . . . . . . . . 6 iL1 . . . . . . 1 . . 1 1 . . 2 . . 2 . . . . . . . . . . . . . . . . . . . 7 iL2 . . . . . . . 1 . . . . 2 . . . . 2 . . . . . . . . . . . . . . . . . . 5 iL3 . . . . . . . . 1 . . . . . 2 . . . . . . . . . . . . . . . . . . . . . 3 iL4 . . . . . . . . . . . 1 . . . 2 . . . . . . . . . . . . . . . . . . . . 3 In1 . . . . . . . . . . . . . . . . . . 1 1 . . 1 1 1 . . . 1 . . . . . . . 6 In2 . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . 1 Is1 1 . 1 1 1 . . . 1 1 1 . 1 1 . . . . 2 2 2 1 . 1 1 1 1 2 . . . . 1 . 1 1 25 Is2 . 1 . . . 1 . 1 . . . 1 . . 1 . 1 1 . . . . 1 . . . . . 2 2 . 1 . 1 . . 14 Is3 . . . . . . 1 . . . . . . . . 1 . . . . . . . . . . . . . . 1 . . . . . 3 iT1 . 1 1 1 1 1 3 . . . . . 2 2 . . . . . . . . . . . . . . . . 1 1 . 1 1 1 17 iT2 . . . . . . . 3 3 3 . . . . 2 2 2 . . . . . . . . . . . . . . . 1 . . . 16 iT3 1 . . . . . . . . . 3 . . . . . . 2 . . . . . . . . . . . . . . . . . . 6 iT4 . . . . . . . . . . . 3 . . . . . . . . . . . . . . . . . . . . . . . . 3 Lg1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 6 Lt1 . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 . . . . . . . . . 3 mO1 . . . . . . . . . . . . . . . . . 1 . . . . . . . . . 1 . . . . . . . . 2 Mt1 . . . . . . . . . . . . . . . . . . 5 4 5 . . . . . . . . . . . . . . . 14 Mt2 . . . . . . . . . . . . . . . . . . . . . 4 4 . . . . . . . . . . . . . 8 Mt3 . . . . . . . . . . . . . . . . . . . . . . . 4 4 5 5 4 . . . 4 . . . . 26 Mt4 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 5 4 . 4 . . . 22 Mt5 . . 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 4 4 16 Mt6 . 4 . . 4 4 5 5 5 . . 5 . . . . . . . . . . . . . . . . . . . . . . . . 32 Mt7 . . . 4 . . . . . 5 5 . . . . 5 . . . . . . . . . . . . . . . . . . . . 19 Mt8 . . . . . . . . . . . . 5 5 5 . . 4 . . . . . . . . . . . . . . . . . . 19 Mt9 . . . . . . . . . . . . . . . . 4 . . . . . . . . . . . . . . . . . . . 4 Mz1 . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 18 Ps1 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Rl1 1 1 1 1 1 . 1 . . 1 . 1 1 1 . . . 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . . 24 Rl2 . . . . . 1 . 1 . . . . . . 1 1 1 . . . . . 1 . . . . . 1 . . . . 1 1 1 10 Rl3 . . . . . . . . 1 . 1 . . . . . . . . . . . . . . . . . . . . . . . . . 2 Rm1 . . . . . . . . . . . . . . . . . . 4 . 4 . . . . . . . . . . . . . . . 8 Rm2 . . . . . . . . . . . . . . . . . . . 4 . 4 . 4 . . . . 4 . 4 . . . . . 20 Rm3 3 3 . . . . . . . . . . . . . . . . . . . . 4 . 4 4 4 . . . . . . . . . 22 Rm4 . . 3 . 3 . . 3 . 3 . . . . . 3 . . . . . . . . . . . 5 . . . 4 . . . 4 28 Rm5 . . . 3 . . 3 . 3 . 3 3 3 3 . . 3 . . . . . . . . . . . . 4 . . 4 4 4 . 40 Rm6 . . . . . 3 . . . . . . . . 3 . . 3 . . . . . . . . . . . . . . . . . . 9 rO1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . . . . . . 1 TI1 . 1 1 1 1 . . . . . . . . . . . . . 1 . 1 . 1 1 1 1 1 1 . . . . 2 2 2 . 18 TI2 1 . . . . . . . . . . . . . . . . . . 1 . 1 . . . . . . 1 1 2 2 . . . 2 11 TI3 . . . . . 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 A B C D E F A B C D E F A B C D E F A B C A B C A B C A B C A B C D E F + 10__________11__________12__________ 5____ 6____ 7____ 8____ 9__________ Total 31 31 31 29 29 29 29 29 29 27 26 28 31 31 31 31 31 31 1069 31 31 31 29 29 29 29 29 29 26 28 28 31 31 31 31 31 31
Imaginând unele programe de testare – de exemplu, unul care să producă din GMP, orarul unei clase indicate – ne putem convinge că (dacă readăugăm "Dirigenţiile") încadrarea la care am ajuns mai sus corespunde orarului iniţial "Orarul general clase", în privinţa repartizării obiectelor pe zile şi ore; însă desigur că nu am nimerit încadrarea reală a profesorilor pe clase – avem doar o încadrare „brută” a unor presupuşi profesori, necesitând anumite ajustări pentru a îndrepta unele defecte.
De exemplu, să observăm orele de "Bio": ele sunt repartizate pe 4 profesori, câte 24, 23, 7 şi 1; ar trebui să vedem care clase le putem trece de la "Bi1" şi "Bi2", la "Bi3" şi cui putem atribui ora existentă la "Bi4" – încât să avem 3 profesori de "Bio", cu 18 sau 19 ore fiecare.
La unele obiecte, trebuie chiar să adăugăm un profesor; de exemplu, la "Fiz" avem "Fz3" cu 44 de ore; fiindcă ceilalţi de la "Fiz" au deja un număr rezonabil de ore, probabil că soluţia cea mai bună constă în a adăuga un al 5-lea profesor de "Fiz" (în loc de a completa orele unora cu anumite ore de la "Fz3").
În schimb, la "Rom", putem trece unele clase de la "Rm5" (care are 40 de ore, pe încadrarea „brută”) la ceilalţi profesori de "Rom".
Asemenea ajustări – pentru a păstra corespondenţa pe obiecte cu "Orarul general clase" iniţial – trebuie să ţină seama totdeauna de valorile zi şi oră din GMP, asociate claselor pe care încercăm să le trecem de la un profesor la altul, pe obiectul respectiv şi ar exista foarte multe posibilităţi de ajustare, fiecare conducând la câte o încadrare posibilă, a profesorilor pe clase.
Concluzie
De obicei, elaborarea orarului şcolar pleacă de la încadrarea pe clase a profesorilor, rezultând în fiecare an câte un nou orar, distinct în toate privinţele faţă de orarul vechi. Din cele de mai sus rezultă o nouă perspectivă de lucru, pentru cazul când structura de clase şi obiecte este cam aceeaşi cu cea din anul precedent: putem pleca de la orarul pe clase şi obiecte existent – determinând automat (prin secvenţe de program precum cele redate mai sus) o schemă de încadrare a profesorilor pe clase care să corespundă (pe obiecte) orarului existent; este relativ uşor de cizelat schema de încadrare obţinută, ţinând seama de câţi profesori şi de ce specialităţi avem în anul şcolar curent.
Orarul pe obiecte devine constant; ce s-ar schimba de la un an la următorul – păstrând cam acelaşi orar pe clase şi obiecte – este încadrarea pe clase a profesorilor.
vezi Cărţile mele (de programare)