Experimente sugestive asupra grafului calului
[1] Experimente de grafică folosind R (dec. 2016…)
Graful calului are ca vârfuri câmpurile tablei de șah, $\{(i,j): 1≤i,j≤8\}$; acestea sunt indexate de obicei prin 1..64, începând fie din colțul stânga-jos ("a1"), fie din colțul stânga-sus ("a8") și parcurgând fiecare linie de la stânga spre dreapta. Vârfurile $(i_1,j_1)$ și $(i_2,j_2)$ sunt adiacente dacă fie $|i_1-i_2|=1$ și $|j_1-j_2|=2$, fie $|i_1-i_2|=2$ și $|j_1-j_2|=1$ (relații care definesc mutarea calului de pe un câmp $(i_1,j_1)$ pe un câmp $(i_2,j_2)$).
Matricea de adiacență are 64×64 valori 0 sau 1 (dar pe fiecare linie/coloană avem cel mult opt valori 1); desigur, nu este necesar să calculăm pentru toate perechile de vârfuri…
Este ușor de văzut că mutările de cal de pe câmpurile care formează centrul lărgit (din careul "c3"--"f3"--"f6"--"c6") acoperă toate câmpurile tablei, cu excepția celor 4 colțuri:
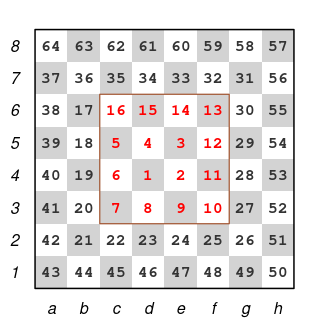
Ca și în jocul de șah, câmpurile centrale au rolul primordial și pare firesc (deși oarecum contrar uzanțelor) să indexăm câmpurile (vârfurile grafului) ca în diagrama redată mai sus: am plecat de pe câmpul central "d4" și am spiralat în jurul acestuia, în sens antiorar.
De observat (poate în avantajul unor algoritmi specifici) că astfel, pe graful calului vârfurile apar cu câteva excepții, în ordine descrescătoare a gradelor: vârfurile 1..16 au gradul 8; apoi 17..36 au gradul 6 (exceptând „colțurile” 21, 26, 31, 36 care au gradul 4), ș.a.m.d.
În principiu, cu această indexare (spiralată în jurul centrului) constituirea matricei de adiacență a grafului calului se simplifică: avem de considerat numai cele 16 câmpuri ale centrului lărgit, fără griji că săritura curentă ar ieși în afara tablei; doar că astfel, rămân neînregistrate adiacențele între vârfuri corespunzătoare câte două la câmpuri exterioare centrului lărgit – și rămâne de văzut cum le-am adăuga, cât mai simplu.
Desigur, numai „în principiu” putem vorbi de simplificări… Mai întâi, pentru fiecare index 1..64 avem de stabilit linia și coloana corespunzătoare câmpului desemnat prin acel index (fiindcă destinația calului depinde totuși de linia și coloana curentă).
Să observăm că plecând de la valorile 4 și 5 existente pentru câmpul de index 1 – socotind pe tablă de la stânga spre dreapta și de sus în jos – indicii de coloană și de linie cresc sau scad cu 1, 2, ..., 7, pe măsură ce avansăm în spirală pe diagrama de mai sus – până ce se ajunge la coloana 8, respectiv la linia 1:
$$4\overset{+1}{\rightarrow}5\overset{-2}{\rightarrow}3\overset{+3}{\rightarrow}6\overset{-4}{\rightarrow}2\overset{+5}{\rightarrow}7\overset{-6}{\rightarrow}1\overset{+7}{\rightarrow}8\\ 5\overset{-1}{\rightarrow}4\overset{+2}{\rightarrow}6\overset{-3}{\rightarrow}3\overset{+4}{\rightarrow}7\overset{-5}{\rightarrow}2\overset{+6}{\rightarrow}8\overset{-7}{\rightarrow}1$$Interpretând aceste formule, constituim un „tabel” idx care indică pentru fiecare index $V=1..64, linia $R și coloana $C ale câmpului corespunzător pe tabla 8×8:
idx <- matrix(0, nrow = 64, ncol = 2, byrow = TRUE) %>% as.data.frame() %>% setNames(c("R", "C")) r1 <- 5; c1 <- 4 # linia și coloana câmpului de index 1 idx[1, ] <- c(r1, c1) i <- 2 for(p in 1:7) { s <- if(p %% 2) 1 else -1 for(h in 1:p) { # incrementează/decrementează coloana, de p ori c1 <- c1 + s idx[i, ] <- c(r1, c1) # linia și coloana câmpului de index i i <- i + 1 } for(h in 1:p) {# decrementează/incrementează linia, de p ori r1 <- r1 - s idx[i, ] <- c(r1, c1) # linia și coloana câmpului de index i i <- i + 1 } } idx[58:64, 1] <- 1 # completează pentru câmpurile rămase pe linia 1 idx[58:64, 2] <- 7:1 idx$V <- 1:64 # indecșii câmpurilor
Obs. Pentru a construi diagrama redată mai sus, am plecat de la o matrice M de tip 8×8 și pentru fiecare linie (R,C,V) din tabelul idx constituit mai sus, am înscris M[R, C] = V – apoi, am folosit programul de redare a tablei din [1] (cu mici adaptări).
Trebuie să fie un alt prilej, simplificarea algoritmului reflectat în secvența de mai sus, pentru a genera cât mai concis o matrice spiralată, de orice ordin…
Să constituim deocamdată acea porțiune a matricei de adiacență care corespunde mutărilor de pe cele 16 câmpuri ale centrului lărgit.
Prevedem matricea-șablon jump conținând cele 8 salturi pe linie și coloană, specifice mutării calului, care sunt posibile de pe câmpul curent; adunând jump vectorului (R, C) preluat de pe linia din idx corespunzătoare vârfului curent i=1..16 (al centrului lărgit) – obținem matricea de 8 linii conținând coordonatele câmpurilor pe care poate muta calul; filtrând tabelul idx pentru fiecare dintre aceste câmpuri, găsim (din coloana $V) vârfurile adiacente cu vârful curent i și înscriem 1 pe locurile corespunzătoare din matricea de adiacență:
A <- matrix(0L, nrow = 64, ncol = 64, byrow = TRUE) # matricea de adiacență jump <- matrix(c(1,2, 2,1, 1,-2, -1,2, -2,-1, 2,-1, -1,-2, -2,1), nrow = 8, ncol = 2, byrow = TRUE) # deplasamente linie,coloană (Cal) for(i in 1:16) { flj <- jump # obținem câmpurile pe care poate sări calul de pe câmpul de index i flj[, 1] <- flj[, 1] + idx$R[i] flj[, 2] <- flj[, 2] + idx$C[i] for(k in 1:8) { J <- idx %>% filter(R == flj[k, 1] & C == flj[k, 2]) %>% pull(V) # indecșii celor 8 adiacenți ai vârfului curent i A[i, J] <- A[J, i] <- 1L } }
Pentru o mică verificare, să listăm adiacenții nodului 1, respectiv 34:
> which(A[1, ] == 1) [1] 10 12 14 16 18 20 22 24 > which(A[34, ] == 1) [1] 3 5 13 # lipsesc 59, 63 și 17
Nodul 34 este extern centrului 1..16, încât secvența de mai sus nu a putut înregistra și adiacența acestuia cu nodurile 59, 63, 17 aflate și acestea, în exteriorul centrului.
Pentru a depista adiacenții rămași ai vârfurilor externe centrului, putem parcurge subsetul rem al liniilor din idx cu $V > 16; pentru linia curentă de rang i din rem, adiacenții nodului V de pe această linie sunt valorile $V de pe liniile aflate dedesubtul liniei curente, pentru care valorile $R și $C se pot deduce printr-o săritură de cal de pe câmpul (R, C) al liniei i:
rem <- idx %>% filter(V %in% 17:64) for(i in 1:nrow(rem)) { from <- rem$V[i] r <- rem$R[i]; k <- rem$C[i] To <- rem %>% filter(V > from) %>% mutate(dr = abs(R-r), dk = abs(C-k)) %>% filter(dr == 1 & dk == 2 | dr == 2 & dk == 1) %>% pull(V) # indecșii câmpurilor atacate de pe indexul 'from' A[from, To] <- A[To, from] <- 1L }
Pentru verificare, putem afișa în final gradele vârfurilor:
> sapply(1:64, function(i) sum(A[i, ])) %>% setNames(as.character(1:64)) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 6 6 6 6 4 6 6 6 6 4 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 6 6 6 6 4 6 6 6 6 4 3 4 4 4 4 3 2 3 4 4 4 4 3 2 3 4 53 54 55 56 57 58 59 60 61 62 63 64 4 4 4 3 2 3 4 4 4 4 3 2
Pentru o mică aplicație, să considerăm – prin pachetul igraph – graful cu matricea de adiacență determinată mai sus:
library(igraph) Kn <- graph_from_adjacency_matrix(A, mode="undirected") # "Knight graph"
Fiindcă vârfurile au fost indexate în spirală începând din centrul tablei, putem specifica imediat subgraful indus de vârfurile exterioare centrului lărgit:
G <- induced_subgraph(Kn, V(Kn) > 16) V(G)$name <- as.character(17:64)
Subgraful G are 48 de vârfuri, indexate prin 1..48; prin atributul $name am păstrat „numele” inițiale din graful Kn, '17'..'64'.
Vrem să evidențiem faptul (nu prea greu de constatat și manual, pentru tabla obișnuită 8×8) că G este format din două drumuri disjuncte, care pleacă – fiecare, într-un același sens – din colțuri alăturate ale tablei (64 și 57) și au aceeași lungime (24):

Pentru aceasta, putem pleca de la igraph::all_simple_paths(), care ne dă lista tuturor căilor între vârfurile indicate, cu lungimea maximă fixată:
pt1 <- all_simple_paths(G, from = "64", to = "37", cutoff = 24) pt2 <- all_simple_paths(G, from = "57", to = "56", cutoff = 24)
Listele rezultate conțin căi de câte o aceeași lungime (pară, desigur):
> sapply(pt1, length) %>% table() 4 8 10 12 14 16 18 20 22 24 # lungime 2 4 2 14 32 108 358 690 1142 1700 # număr căi
Filând printre căile de lungime 24 din lista pt1, nu-i greu să depistăm până la urmă una care „curge” în sens orar (cea trasată cu roșu, pe diagrama de mai sus):
#[[3990]] #+ 24/48 vertices, named, from de9fc50:
[1] 64 35 60 31 54 27 50 25 46 21 40 17 62 33 58 55 28 51 48 23 44 41 18 37
Căutăm în cealaltă listă pt2, o cale de lungime 24 care să nu aibă vârfuri comune cu drumul din pt1 tocmai evidențiat mai sus:
P1 <- pt1[[3990]] %>% as_ids() for(i in 1:length(pt2)) { P2 <- pt2[[i]] %>% as_ids() if(length(P2) != 24) next if(length(intersect(P1, P2)) == 0) { print(i) print(P2) } }
Dintre cele două căi P2 rezultate astfel, o alegem pe cea (marcată cu albastru pe diagrama de mai sus) care păstrează un același sens (cel antiorar) al mutărilor succesive ale calului.
Pentru a și trasa căile P1 și P2, pe diagrama plotată anterior (prin programul din [1]) – speculăm iarăși tabelul idx (transformând $R și $C în ordonate și abscise ale centrelor câmpurilor):
P2 <- pt2[[3885]] %>% as_ids() %>% as.integer() P1 <- as.integer(P1) idx$R <- 9 - idx$R # inversează ordinea liniilor tablei idx$R <- 8*idx$R - 4 # avem câte 8 "pixeli" pentru fiecare câmp (v. [1]) idx$C <- 8*idx$C - 4 y <- idx$R[P1] # coordonatele centrelor pătrățelelor x <- idx$C[P1] lines(x, y, col="red", lwd=0.8) # trasează drumul P1 y <- idx$R[P2] x <- idx$C[P2] lines(x, y, col="blue", lwd=0.8) # trasează drumul P2
Mulțimea D a celor 20 de vârfuri asociate centrului lărgit 1:16 și colțurilor tablei constituie o mulțime de vârfuri dominantă a grafului calului: orice vârf fie face parte din D – și eventual, nu are adiacenți în D, cum este cazul colțurilor tablei – fie are măcar un adiacent în D (cum este cazul tuturor celor 60 de vârfuri diferite de colțurile tablei).
Dar D nu este o mulțime dominantă minimală; se știe (v. OEIS) că numărul minim de cai necesar pentru a ocupa sau ataca orice câmp al tablei 8×8 este 12 – iar aceștia pot fi plasați de exemplu, astfel: întâi așezăm câte un cal pe câmpurile careului 7--10--13--16 (care formează laturile centrului lărgit, cu 12 câmpuri); apoi, pe fiecare latură și într-un același sens, mutăm al 3-lea cal (dintre cei 4 ai laturii respective) dincolo de colțul cel mai apropiat, pe câmpul vecin acestuia.
Desigur, plecând de la o asemenea mulțime dominantă minimală, ar fi mai ușor de constituit matricea de adiacență a grafului, decât plecând ca mai sus de la centrul lărgit (fiindcă sunt 12 și nu 16 (sau 20), vârfuri „de bază” și nu ar mai fi de tratat separat vreo mulțime de vârfuri „exterioară”). Dar alta este problema interesantă, care a apărut: „simplificarea” și generalizarea algoritmului conturat mai sus pentru a genera matrici spiralate…
vezi Cărţile mele (de programare)