Generarea matricelor spirale și indexarea în spirală (I)
Cităm un enunț întâlnit în diverse culegeri (sau site-uri) de „probleme de informatică”:
„Se citeste o matrice patratica de dimensiune n*n cu elemente numere naturale. Sa se afiseze elementele matricei in spirala pornind de la elementul a[0][0] in sensul acelor ceasornicului.”
sau, formulat mai concis (totuși… corect: nu lipsesc litere – cum mai sus 'ă', 'ș', 'î'):
"Imprimez une matrice carrée en spirale sans utiliser d'espace supplémentaire"
Pe baza soluțiilor obișnuite, putem clasifica problema ca artificială: servește pentru a exersa instrucțiunea for (pe lângă veșnica „citește de la tastatură” și „afișează pe ecran”) – sau amintind și alte cazuri, servește pentru a exersa o formulă sau o regulă de calcul, aplicarea unei inegalități clasice, sau a unui algoritm uzual, etc.
E greu de înțeles atracția pentru seturi de asemenea exerciții, de abordat cam într-un același mod (și grăbit) și într-un același limbaj…
Problema capătă sens (deschidere) dacă o poți pune în mod firesc, în vreun context cât de cât important sau măcar interesant (dar nu de genul povestioarelor puerile (dar lungi), cum vedeam pe la "olimpiadă", cel puțin prin anii 2000).
În [1] avem un context interesant care sugerează în mod firesc problema de mai sus; iar un context important (chiar bazat pe indexarea în spirală) este spirala lui ULAM.
În principiu, soluționarea implică parcurgerea într-un același sens a marginilor matricei – „tăind” apoi laturile parcurse deja și continuând cât timp mai vedem „laturi”.
Producțiile de secvențe după un anumit șablon (în R: seq(), rep(), etc.) substituie foarte bine, asemenea „parcurgeri” și am putea ajunge, analizând lucrurile, la un program concis.
Analiza lucrurilor
Considerăm matricea (pătratică) în formatul standard de afișare: liniile și coloanele sunt indexate (sau etichetate) prin $1..n$ de sus în jos și respectiv, de la stânga spre dreapta. Avem de spiralat în jurul centrului matricei; alegem sensul antiorar.
Subliniem că în R o matrice este un vector cu atributul "dim" (în care se precizează dimensiunile); de regulă este memorată pe coloane, dar construind-o cu parametrul "byrow", matricea ajunge în formatul „standard” considerat mai sus (pe linii). Uneori este convenabil să simplificăm: o matrice este „un vector – sau o listă – de vectori, toți de același tip (integer, char, etc.) și de aceeași lungime”.
Poziția centrului depinde de paritatea lui $n$. Dacă $n$ este impar, avem un singur câmp egal depărtat de margini; dacă n este par, avem o submatrice 2×2 cu marginile egal depărtate de marginile matricei și alegem drept „centru”, câmpul din stânga-jos al acesteia:
R1 <- n %/% 2 + 1 # linia centrului (indexând de sus în jos) C1 <- if(n %% 2) R1 else R1 - 1 # coloana centrului
Operatorii "%/%" și "%%" realizează operațiile DIV și MOD (v. „teorema împărțirii cu rest”).
Plecând în spirală din centru, avem de mers succesiv în patru direcții: întâi spre dreapta (fiindcă ne-am stabilit sensul antiorar), apoi în sus, spre stânga, respectiv în jos – încheind o „buclă” a spiralei; continuăm la fel pentru a doua buclă, a treia, ș.a.m.d.
Trasarea pe orizontală nu modifică rangul de linie, dar rangul de coloană crește sau descrește după cum ne deplasăm spre dreapta sau spre stânga; pe verticală, rangul de coloană rămâne constant, dar cel de linie crește în jos și descrește în sus.
Să clasificăm numeric, prin $0$, $1$ și $-1$, cele trei comportamente posibile pentru rangul de linie sau coloană ($0$: rangul se păstrează; $1$: crește; $-1$: descrește):
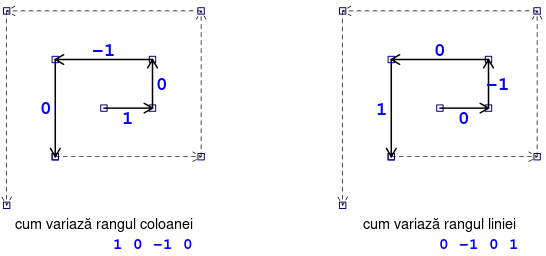
Am reprezentat (prin linii de tip diferit) primele două „bucle” ale spiralei; dacă este completă, o buclă are 4 arce orientate spre dreapta, în sus, spre stânga, respectiv în jos.
Pe fiecare buclă completă avem 4 variații consecutive pentru rangul de coloană (1 0 -1 0) și 4 variații ale rangului de linie, (0 -1 0 1).
Să observăm însă că ultima buclă – care încheie spirala, pentru întreaga matrice – este incompletă; spirala se încheie în colțul din stânga-sus dacă $n$ este par (deci în ultima buclă nu mai avem arcul „în jos”) și se încheie în colțul din dreapta-jos dacă $n$ este impar (deci ultima buclă are numai primul arc, „spre dreapta”).
Câte variații consecutive ale rangului (de coloană) avem, pentru întreaga spirală?
Dacă $n$ este impar, dedesubtul liniei centrale a matricei avem $\frac{n-1}{2}$ linii, deci avem $\frac{n-1}{2}$ capete finale de bucle complete ale spiralei totale și mai trebuie parcursă doar ultima linie, de la stânga spre dreapta. Rezultă că dacă $n$ este impar, avem $\frac{n-1}{2}$ bucle complete și una cu un singur arc "$1$" – deci în total, de-a lungul întregii spirale, avem $\frac{n-1}{2}*4 +1=2n-1$ variații de rang (de linie și respectiv, de coloană). Putem raționa cam la fel pentru $n$ par, iar concluzia finală este că pentru orice $n\ge 3$, numărul total de variații ale rangului (de linie, ca și de coloană) de-a lungul întregii spirale este $2n-1$.
Având cele două secvențe de câte $2n-1$ variații de rang, putem determina coordonatele pentru fiecare câmp prin care trece succesiv spirala, dacă ținem cont și de lungimea fiecărei deplasări (pe orizontală, respectiv pe verticală).
De exemplu, să găsim coordonatele nodului al 7-lea al spiralei – centrul (R1, C1) fiind nodul zero al acesteia; ajungem la nodul 7 după 7 deplasări succesive pe linii și coloane:
R1 0 -1 0 1 0 -1 0 (variația rangului de linie, plecând de la R1) 1 1 2 2 3 3 4 (lungimea fiecărei deplasări orizontale) C1 1 0 -1 0 1 0 -1 (variația rangului de coloană, plecând de la C1) 1 1 2 2 3 3 4 (lungimea fiecărei deplasări verticale)
deci rangul liniei celui de-al 7-lea nod este R1 + (-1)×1 + 1×2 + (-1)×3 = R1-2, iar rangul coloanei este C1 +1-2+3-4=C1-2 (am ignorat deplasările "0", care conservă rangul curent).
Deci avem deocamdată două probleme: să constituim cele două secvențe de câte $2n-1$ variații de rang și să constituim secvența lungimilor deplasărilor respective.
O a treia problemă va decurge din faptul că vrem coordonatele tuturor nodurilor spiralei și nu doar pentru câte un anumit nod (precum în exemplificarea de mai sus).
Să observăm că pentru prima buclă a spiralei, deplasările – numărul de câmpuri, pe fiecare direcție – sunt 1 1 2 2; pentru a doua buclă, deplasările sunt 3 3 4 4; iar ultimul arc, din bucla incompletă finală a spiralei, angajează toate cele $n$ câmpuri ale primei sau ultimei linii a matricei (după cum $n$ este par sau impar).
Prin urmare, secvența deplasărilor se obține repetând de câte două ori fiecare membru al secvenței $1..n$ – păstrând însă numai primele $2n-1$ valori produse astfel.
Primele două probleme se rezolvă (imediat) folosind funcții rep() (cu parametri adecvați):
sp_row <- rep_len(c(0, -1, 0, 1), 2*n-1) # variațiile rangului de linie sp_col <- rep_len(c(1, 0, -1, 0), 2*n-1) # variațiile rangului de coloană dep <- rep(1:n, each = 2, length.out = 2*n-1) # lungimile deplasărilor
Pentru a treia problemă, revenim întâi la exemplificarea de mai sus, pentru a observa o anumită simplificare; în loc să calculăm suma produselor dintre variații (-1 și 1) și lungimile corespunzătoare acestora (cum am făcut mai sus), putem rescrie întâi secvența variațiilor, repetând pe fiecare de câte ori arată lungimea corespunzătoare ei:
R1 0 -1 0 0 1 1 0 0 0 -1 -1 -1 0 0 0 0 (variația pe fiecare câmp, a rangului de linie) C1 1 0 -1 -1 0 0 1 1 1 0 0 0 -1 -1 -1 -1 (variația rangului de coloană)
De observat că după rescriere, secvența variațiilor are ca lungime numărul de câmpuri prin care trece spirala până la nodul al 7-lea.
Însumând, regăsim R1-2 și C1-2 – rangurile de linie și coloană pentru al 7-lea nod al spiralei.
Ca să rescriem secvența sp_row (analog pentru sp_col), repetând fiecare valoare de câte ori arată valoarea de același index din vectorul dep, putem folosi iarăși funcția rep(), angajând (explicit, sau implicit) parametrul times al ei; secvența rezultată după rescriere are $n$×$n$ valori (fiindcă spirala finală trece prin toate celulele matricei) și adăugându-i pe primul loc valoarea R1 – ne rămâne doar să cumulăm pas cu pas valorile respective (folosind cumsum()):
R1 R1-1 R1-1 R1-1 R1 R1+1 R1+1 R1+1 R1+1 R1 R1-1 R1-2 R1-2 ...
și am obținut (deodată, nu în parte) valorile rangului de linie pentru fiecare nod al spiralei.
Deci pentru a treia problemă avem această rezolvare:
ROW <- rep(sp_row, times = dep) # variația rangului de linie pe parcursul spiralării COL <- rep(sp_col, dep) # variația rangului de coloană pe parcursul spiralării N <- n*n ROW <- cumsum(c(R1, ROW))[1:N] # rangul de linie al fiecărui nod al spiralei COL <- cumsum(c(C1, COL))[1:N] # rangul de coloană al fiecărui nod al spiralei
Acum, dacă ar fi să afișăm valorile 1..N (cu N=n×n) spiralând din centrul unei matrice pătratice, putem proceda astfel:
Sp <- matrix(0L, nrow = n, ncol = n, byrow = TRUE) for(i in 1:N) Sp[ROW[i], COL[i]] <- i
De exemplu, pentru $n=5$ și $n=6$ obținem:
[,1] [,2] [,3] [,4] [,5] [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 17 16 15 14 13 [1,] 36 35 34 33 32 31
[2,] 18 5 4 3 12 [2,] 17 16 15 14 13 30
[3,] 19 6 1 2 11 [3,] 18 5 4 3 12 29
[4,] 20 7 8 9 10 [4,] 19 6 1 2 11 28
[5,] 21 22 23 24 25 [5,] 20 7 8 9 10 27
[6,] 21 22 23 24 25 26
Să mai observăm că dacă am vrea ca spirala să plece nu din centrul matricei, ci din colțul care conține cea mai mare valoare – atunci n-avem decât să afișăm (N+1)-Sp (în R avem operații vectorizate: valoarea N+1 este extinsă pe lungimea „vectorului” Sp și apoi se face scăderea, „în paralel”). Iar dacă vrem ca valoarea cea mai mare să fie într-un alt colț (decât dreapta-jos, respectiv stânga-sus) – putem transpune matricea, folosind funcția
Dar… (iarăși) ce sens are, să afișăm valorile 1..N „spiralând în jurul centrului” unei matrice? Poate, dacă ar fi vorba nu de 1..N, ci de elementele unei matrici date?
Sinteza lucrurilor
Firește – avem de strâns într-o funcție independentă, demersurile de mai sus. Dar scopul acestei funcții nu trebuie să fie „afișarea pe ecran”; ea trebuie doar, să furnizeze cumva vectorii ROW și COL – rămânând utilizatorului să-i folosească (iată „a patra” problemă) de exemplu pentru a afișa spiralând din centru, elementele unei matrici date.
Îmbinând pur și simplu, cele de mai sus (fără a căuta simplificări), putem formula funcția:
spiral_walk <- function(n) { R1 <- n %/% 2 + 1 # linia centrului, indexând de sus în jos C1 <- if(n %% 2) R1 else R1 - 1 # coloana centrului N <- n*n # numărul de noduri ale spiralei sp_row <- rep_len(c(0, -1, 0, 1), 2*n-1) # variațiile rangului de linie sp_col <- rep_len(c(1, 0, -1, 0), 2*n-1) # variațiile rangului de coloană dep <- rep(1:n, each = 2, length.out = 2*n-1) # lungimile deplasărilor ROW <- rep(sp_row, dep) # variația prin spiralare a rangului de linie COL <- rep(sp_col, dep) # variația prin spiralare a rangului de coloană ROW <- cumsum(c(R1, ROW))[1:N] # rangul de linie al fiecărui nod al spiralei COL <- cumsum(c(C1, COL))[1:N] # rangul de coloană al fiecărui nod al spiralei data.frame(R = ROW, C = COL, V = 1:N) # tabel de linie/coloană/nod_spirală }
De exemplu spiral_walk(5) va returna rezultatul ultimei „instrucțiuni” pe care o execută – deci un obiect din clasa data.frame, care are forma unui tabel cu 3 coloane (numite "R", "C" și "V") și 25 de linii; prima linie de exemplu, este 3 3 1 – însemnând că vârful 1 al spiralei este în celula din linia 3 și coloana 3 a matricei 5×5.
Dacă vrem neapărat (să zicem, de dragul conciziei – dar poate fi vorba și de eleganță, sau de „bunele practici”), putem reformula astfel:
sp_walk <- function(n) { rep4d <- function(D4) # D4 este un vector cu 4 valori (deplasamente) rep( rep_len(D4, 2*n-1), rep(1:n, each=2, length.out=2*n-1) ) R1 <- n %/% 2 + 1 C1 <- if(n %% 2) R1 else R1 - 1 N <- n*n data.frame(R = cumsum(c(R1, rep4d(c(0,-1,0,1))))[1:N], C = cumsum(c(C1, rep4d(c(1,0,-1,0))))[1:N], V = 1:N) }
Am eliminat variabilele "sp_row" și "sp_col"; valorile lor sunt produse acum apelând funcția internă rep4d() (funcție internă contextului de execuție al funcției sp_walk()). Iar vechile variabile "ROW" și "COL" au fost instanțiate direct, la construcția tabelului returnat.
Acum, dacă M este o matrice n×n și tb este tabelul returnat de sp_walk(n), atunci M[tb$R[i], tb$C[i]] <- tb$V[i] va fixa în celula cu linia și coloana indicate pe a i-a linie din tb, valoarea pentru $V de pe această linie (care poate fi chiar i, din 1..nrow(tb)).
Testare
Ar fi de testat funcția sp_walk() și profităm de aceasta pentru a vedea cum tratăm „a patra” problemă: este dat un vector cu N=n×n elemente – ceea ce echivalează cu a da o matrice n×n – și se cere să afișăm elementele lui plecând în spirală din centrul unei matrice.
Să constituim o matrice 5×5 având ca elemente litere distincte, într-o ordine arbitrară:
Lit <- sample(LETTERS)[1:25] # aranjament aleatoriu al literelor majuscule Data <- matrix(Lit, nrow=5, byrow=TRUE) [,1] [,2] [,3] [,4] [,5] [1,] R M W N E [2,] D O Q C K [3,] S Y X F A [4,] L J P B I [5,] G T H Z V
Obținem prin sp_walk(5) corespondența dintre indecșii nodurilor spiralei și celulele unei matrice 5×5, apoi instanțiem o asemenea matrice M și plasăm literele din vectorul Lit conform acestei cerespondențe:
rcv <- sp_walk(5) M <- matrix("", nrow=5, ncol=5, byrow=TRUE) for(k in 1:25) { i <- rcv$R[k] # corespondența pe celule a indecșilor spiralei j <- rcv$C[k] M[i, j] <- Lit[k] # ( știm că rcv$V[k] este k ) } print.table(M) [,1] [,2] [,3] [,4] [,5] [1,] J L A F X [2,] P E N W Y [3,] B D R M S [4,] I O Q C K [5,] G T H Z V
Desigur, am ales $n=5$ fiindcă nu avem decât 26 de litere standard (pe care R le păstrează în vectorii LETTERS și letters; dacă vrem, putem repeta LETTERS de câte ori este necesar, pentru a testa ca mai sus, de exemplu pentru n=12).
Mai departe, speculând funcția sp_walk() introdusă mai sus, vom viza spirale ULAM.
vezi Cărţile mele (de programare)