Formule versus Algoritm
[1] CONCRETE MATHEMATICS - R. L. Graham, D. E. Knuth, O. Patashnik (Addison-Wesley; 1989, 1994)
[2] OEIS: A296030 Pairs of coordinates for successive integers in the square spiral (counterclockwise)
[3] Generarea matricelor spirale și indexarea în spirală (I și II)
Într-un exercițiu din [1] (3 Integer Functions / Exercises / 40) se cer coordonatele punctelor întregi de pe „spirala pătrată” arătată pe graficul următor:
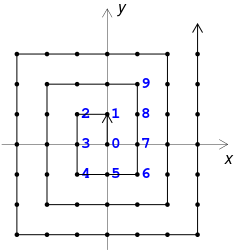
Mai precis, se cere să se demonstreze că abscisele $x(n)$ și ordonatele $y(n)$ ale punctelor marcate cu $n\in\mathbb{N}$ sunt date de formulele:
$$x(n)=(-1)^m((n-m(m+1))\cdot\lceil\lfloor2\sqrt{n}\rfloor\,\text{is even}\rceil + \lceil\frac{1}{2}m\rceil)\\ y(n)=(-1)^m((n-m(m+1))\cdot\lceil\lfloor2\sqrt{n}\rfloor\,\text{is odd}\rceil - \lceil\frac{1}{2}m\rceil)$$unde $m=\lfloor\sqrt{n}\rfloor$ (= max{h | h ≤ n, integer h} = floor(n)).
Pentru același context, sunt deduse formule similare și în alte locuri (v. StackExchange), iar secvența absciselor și ordonatelor punctelor spiralei pătratice este consemnată pe OEIS, în [2]. Apar și programe (în diverse limbaje) care produc secvențele respective – dar de obicei, doar traduc mot-a-mot formulele matematice pentru $x(n)$ și $y(n)$.
Exercițiul redat mai sus nu este totuși, decât o problemă artificială (dar interesantă): este util probabil, pentru a exersa lucrul cu „partea întreagă” (pentru care și în limbajele de programare, avem două funcții: ceil() pentru $\lceil\,\rceil$ și floor() pentru $\lfloor\,\rfloor$). În realitate, „spirala pătrată” vizată mai sus este legată (exclusiv, se pare) de matricea-spirală a lui Ulam (v. [3]), iar aceasta implică nu coordonate $(x,y)$, ci (direct) indecșii de linie și coloană.
Este drept că putem imita calculul coordonatelor $(x(n),y(n))$, obținând formule similare pentru rangurile de linie și coloană dintr-o matrice-spirală Ulam; iar apoi, n-am avea decât să formulăm o funcție (într-un limbaj sau altul) row_and_col() care pentru un $n$ dat ca parametru, să furnizeze pe baza acestor formule, perechea de indecși (linie și coloană) care localizează numărul $n$ în matricea respectivă.
Desigur, dacă ar fi vorba de matrici-spirale cu până pe la 100 de elemente, atunci nici nu am avea nevoie de programare cu row_and_col(); dar de fapt, tocmai scriind o asemenea matrice mică – în timp ce asista la o expunere academică „lungă și plicticoasă” – S. Ulam și-a pus problema dacă numerele prime sunt aleatoriu dispuse, pe „spirala” respectivă. Bineînțeles că investigarea experimentală a distribuției numerelor prime implică matrici-spirale cât se poate de mari – încât o funcție ca row_and_col() devine probabil, necesară.
Pentru a genera o matrice-spirală M cât mai mare, de exemplu de tip 300×300 – cu scopul de a marca numerele prime conținute și a descoperi eventual anumite șabloane formate de acestea – am folosi row_and_col(), probabil cam așa:
for n = 1..300^2 {
(R, C) = row_and_col(n)
M[R, C] = n
}
păstrând numerele respective, sau – dacă vrem doar să marcăm numerele prime (ori poate, pe cele de vreun alt tip, de exemplu, „numerele triunghiulare”) – cam așa:
for n = 1..300^2 {
if(n este PRIM) {
(R, C) = row_and_col(n)
M[R, C] = TRUE ## sau direct: M[row_and_col(n)] = TRUE
}
}
Asemenea secvențe de program sunt frecvent întâlnite, dar nu-i nimic de lăudat: funcția row_and_col() este apelată pentru fiecare $n$ în parte (de foarte multe ori)…
Parcă lucrurile ar sta mai bine, dacă am genera în prealabil, vectorul W al tuturor componentelor (R, C) necesare – atunci, în "for"-ul de mai sus va fi de accesat acest vector, în loc de a apela mereu row_and_col():
M[W[n]] = TRUE
Dar… pentru a constitui vectorul W, n-ar trebui deasemenea, să apelăm row_and_col() pentru fiecare $n$ în parte?
Rezultă această problemă de programare: putem constitui vectorul W „deodată”, fără a apela vreo funcție row_and_col() „pentru fiecare $n$ în parte”? Adică, putem determina simultan (sau „în paralel”) toate valorile (R, C), în loc să le aflăm una câte una?
Deci în loc de formulele de calcul a valorii (R, C) corespunzătoare fiecărei valori $n$ date, ar fi de căutat un algoritm prin care să producem întreaga secvență a acestor valori…
În [3] am ajuns la un asemenea algoritm, prin care producem „deodată” secvența valorilor R și deasemenea, secvența valorilor C; completăm aici, explicitând mai bine algoritmul respectiv și ilustrându-l pe un caz concret.
Preliminarii
Matricele-spirale Ulam sunt studiate cu scopul de a dezvălui proprietăți ale distribuției numerelor prime – deci sunt de vizat matrici mari (și nicidecum, de tip 10×10), astfel că nu prea contează dacă dimensiunea este 300, sau este 301…
Vom viza o matrice M de tip n×n, cu n impar – ceea ce ne va simplifica puțin, descrierea algoritmului; de exemplu „centrul” matricei conține în acest caz un singur câmp (și nu 4 câmpuri, ca în cazul când n ar fi par).
Redăm pentru orientare, o matrice-spirală Ulam cu n=7:
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 37 36 35 34 33 32 31
[2,] 38 17 16 15 14 13 30
[3,] 39 18 5 4 3 12 29
[4,] 40 19 6 1 2 11 28
[5,] 41 20 7 8 9 10 27
[6,] 42 21 22 23 24 25 26
[7,] 43 44 45 46 47 48 49
Pentru această matrice, nodurile spiralei Ulam sunt numerele naturale consecutive 1..49, amplasate plecând din centrul matricei (câmpul din linia 4, coloana 4) și „spiralând” în jurul centrului, în sens antiorar; am marcat nodurile primei bucle a spiralei (v. [3]), buclă care poate fi descrisă pentru a evidenția schimbarea direcției, prin 1 → 2 → 3 → 5 → 7; a doua buclă pleacă din 7, merge orizontal până în 10, continuă vertical până în 13, apoi orizontal până în 17 și vertical până în capătul ei final 21.
Algoritmul nostru speculează această observație: pe fiecare buclă se merge succesiv pe 4 direcții, iar fiecare dintre acestea fie păstrează, fie crește, fie descrește (de câte un anumit număr de ori) rangurile de linie și de coloană ale câmpului curent; cumulând succesiv creșterile și descreșterile, putem afla rangurile de linie și coloană corespunzătoare oricăruia dintre nodurile spiralei.
Iar dacă în limbajul ales pentru implementarea algoritmului, dispunem de operații care produc „deodată” (și nu chiar, pas cu pas) secvențe de o anumită lungime și cu o anumită structură, atunci vom putea obține „deodată” întreaga secvență a rangurilor de linie (respectiv, de coloană), corespunzătoare nodurilor succesive prin care trece spirala.
Algoritm de mapare pe linii (coloane) a nodurilor spiralei Ulam
Să clasificăm numeric variația rangului de linie sau coloană, astfel:
0 pentru cazul când pe direcția curentă, rangul nu se modifică;
1 pentru cazul când pe direcția curentă rangul crește;
-1, dacă rangul descrește de-a lungul direcției curente.
Pe fiecare buclă, variația rangului de linie este dată de vectorul 0 -1 0 1, iar variația rangului de coloană este dată de vectorul 1 0 -1 0.
Pas 1: repetăm elementele vectorului-variație până la lungimea 2n-1.
Acest prim pas decurge din faptul ușor de dovedit (v. [3]) că în total, până la capătul final al spiralei, avem exact (2n-1) „variații”.
Pentru ilustrare, efectuăm "Pas 1" pentru $n=5$:
pentru rangul de linie obținem secvența de 9 valori: 0 -1 0 1 0 -1 0 1 0
pentru rangul de coloană: 1 0 -1 0 1 0 -1 0 1
În secvența rezultată, primele 4 variații corespund primei bucle a spiralei, următoarele 4 – celei de-a doua, ș.a.m.d. Ultima buclă (care „încheie” matricea) este incompletă: dacă $n$ este impar, ultima buclă are numai primul dintre cele 4 segmente (corespunzător parcurgerii de la stânga spre dreapta a ultimei linii a matricei, prin care rangul de linie se păstrează, iar cel de coloană crește cu câte o unitate); dacă $n$ este par, atunci ultima buclă are numai primele trei segmente (și se vede că este mai ușor de ilustrat, cazul când $n$ este impar).
Pas 2: repetăm de câte două ori, valorile 1..n, până avem astfel 2n-1 valori.
Prin aceasta evidențiem pentru fiecare buclă, numărul de câmpuri de pe fiecare direcție; prima buclă parcurge orizontal (de la stânga spre dreapta) 1 câmp, apoi vertical (de jos în sus) 1 câmp, apoi orizontal (de la dreapta spre stânga) 2 câmpuri și vertical (de sus în jos) 2 câmpuri; pentru a doua buclă, secvența respectivă este 3 3 4 4; ș.a.m.d.
Pentru ilustrare, efectuăm "Pas 2" pentru $n=5$:
1 1 2 2 3 3 4 4 5
Secvențele constituite prin "Pas 1" și "Pas 2" permit calculul rangurilor de linie și coloană pentru fiecare nod al spiralei: vedem câte bucle se fac până la nodul respectiv și însumăm produsele dintre valorile de același index din cele două secvențe (v. [3] pentru un exemplu). Totuși să nu procedăm așa, fiindcă ar însemna să calculăm pentru fiecare nod în parte și nu „deodată” pentru toate nodurile spiralei.
Pas 3: rescriem vectorii din "Pas 1", repetând fiecare element de câte ori arată în paralel vectorul din "Pas 2"; prefixăm secvența rezultată, cu rangurile centrului.
Pentru $n=5$, centrul este în linia 3 și coloana 3; efectuăm "Pas 3", pentru rangurile de linie, respectiv de coloană:
3 0 -1 0 0 1 1 0 0 0 -1 -1 -1 0 0 0 0 1 1 1 1 0 0 0 0 0
3 1 0 -1 -1 0 0 1 1 1 0 0 0 -1 -1 -1 -1 0 0 0 0 1 1 1 1 1
Secvențele rezultate în "Pas 3" au lungimea $n^2+1$ ("+1" fiindcă am inclus și rangul centrului); însumând valorile până la un index oarecare, obținem rangurile de linie și coloană pentru nodul corespunzător acelui index.
Pas 4: pe vectorii din "Pas 3", calculăm (din aproape în aproape) „sumele cumulate” (pentru fiecare element, se însumează valorile care îl preced), reținând numai primele $n^2$ dintre acestea (excluzând eventual, ultimul element – care ar extinde spirala în afara matricei date).
Pentru ilustrare, efectuăm "Pas 4" pentru $n=5$ (pentru linii, respectiv coloane):
3 3 2 2 2 3 4 4 4 3 2 1 1 1 1 1 2 3 4 5 5 5 5 5 5
3 4 4 3 2 2 2 3 4 5 5 5 5 4 3 2 1 1 1 1 1 2 3 4 5 (urmează 6, extinzând spirala)
Algoritmul este încheiat: pentru nodul de index $k=1..n^2$ al spiralei, avem rangul de linie și de coloană la indexul $k$ din cei doi vectori rezultați în "Pas 4".
Algoritmul prezentat este ușor de implementat (concis) în R (v. funcția sp_walk() din [3]), fiindcă dispunem de operatori și funcții pentru a produce secvențe cu o anumită structură (":", rep(), rep_len()), precum și de funcții de însumare precum cumsum(); în plus, operațiile sunt în general, „vectorizate” (decurg „în paralel”, pentru toți indecșii vectorilor implicați).
vezi Cărţile mele (de programare)