Instrumentarea reducerii ferestrelor din orar
[1] Orar pentru lecţiile unei zile (I) şi (II)
Prin programul daySchoolSchedule.R din [1] obţinem (repede) un orar (sau mai multe) în care numărul de ferestre (pentru şcoli cu un singur schimb) este cel mult 15% din numărul tuturor lecţiilor zilei (iar „per profesor”, numărul de ferestre este 0, 1, sau 2).
Muncind (chiar şi două-trei ore) pe vreo aplicaţie interactivă (v. /dayRecast şi /recast), am putea rearanja orele cam cum dorim, reducând pe cât putem şi numărul de ferestre; dar vrem şi un program prin care să reducem „automat”, cât mai mult, numărul ferestrelor.
Aici iniţiem deocamdată, un asemenea program – specificând (în R) o operaţie de modificare a orelor alocate lecţiilor, pe care o susţinem şi vizual, arătând că ea se poate deriva din conceptul de lanţ Kempe al teoriei colorării hărţilor.
Matricea orelor şi evidenţierea ferestrelor
# recast.R library(tidyverse) TMT <- read_csv("orar.csv", col_types = "cccccccc")
Pentru exemplificări folosim un set de date deja considerat anterior, conţinând un orar pentru 241 de lecţii (într-o zi), cu 68 profesori şi 41 de clase (nu 40, cum indicasem în [1]; sunt 8 nivele de clasă, cu subnivelele A..E, dar… avem şi clasa 8F).
> slice_sample(TMT, n=5) # selectează aleatoriu 5 linii (şi afişează în consolă) # A tibble: 5 x 8 prof `1` `2` `3` `4` `5` `6` `7` <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> 1 P06 - - 12A 9E 12E 12D - # 0 ferestre 2 P57 5A 6B 5D - - - - 3 P30 5D 8F - 6B 5E - - # o fereastră (în ora `3`) 4 P25 12C - - 5D 7E 9B - # două ferestre (consecutive) 5 P47 7E 8E 8A - - - -
Pentru a referi clasele (şi ferestrele) din ora a 3-a de exemplu, ar trebui să folosim TMT[, 4], sau TMT$"3". Este mult mai comod (dar şi mai eficient) să lucrăm cu matricea orelor – păstrând profesorii nu într-o coloană de date, ci doar ca nume de linii:
MXT <- as.matrix(TMT[, 2:ncol(TMT)]) row.names(MXT) <- TMT$prof # selectează aleatoriu 5 linii din matrice: > print.table(MXT[sample(nrow(MXT),5), ]) # 1 2 3 4 5 6 7 # P55 - - 8C - 12A 5D - ## cu şablonul binar '0110100' (pe orele 7..1) # P28 11B - 6A 12B 10C 9C - ## '0111101' # P31 - - 6C 9B 11C 5E - # P29 8E 8A - 12C - - - # P02 - - 9C 7C 6E 6C 9B
Imaginăm întâi nişte funcţii prin care să evidenţiem şi să contorizăm ferestrele; avem de considerat nu numai matricea iniţială MXT, dar şi matrici orare 'morr' provenite din aceasta (sau apoi, una din alta) prin diverse redistribuiri ulterioare de clase şi ferestre.
Următoarea funcţie produce un vector prin care fiecărui profesor îi este asociat şablonul binar al orarului său (orei 1..7 îi asociem bitul de rang 0..6, cu valoarea '0' pentru „fereastră” (şi pentru orele libere, iniţiale sau finale) şi '1' pentru „clasă”):
bin_patterns <- function(morr) { # şabloanele binare ale orarelor profesorilor apply(morr, 1, function(L) { byte <- 0L for(j in 1:ncol(morr)) if(L[j] != '-') byte <- bitwOr(byte, bitwShiftL(1, j-1)) byte }) }
Astfel, pentru "P55 - - 8C - 12A 5D -" avem şablonul binar '0110100'=32+16+4=52.
Pentru evidenţierea şi contorizarea ferestrelor introducem funcţile:
whereOne <- function(w) # indecşii biţilor '1' dintr-un şablon orar which(bitwAnd(w, c(1, 2, 4, 8, 16, 32, 64)) > 0) nHoles <- function(w) { # Numărul biţi '0' între biţi '1' ("ferestre") bits <- whereOne(w) n <- length(bits) bits[n] - bits[1] + 1 - n } nGaps <- function(bin_patt) # 'bin_patt': vectorul şabloanelor orare sum(unlist(lapply(bin_patt, nHoles))) # numărul ferestrelor din orar
De exemplu, orarul nostru (obţinut întâmplător în 3 minute, prin programul din [1]) are iniţial, 25 de ferestre (rezonabil ar fi, să fie cel mult 15):
> print(nGaps(bin_patterns(MXT))) [1] 25 # numărul iniţial de ferestre
Operaţii de repoziţionare în orar, a claselor
Într-un orar nu există suprapuneri: fiecare clasă apare o singură dată în oricare coloană (sau cel mult o singură dată, dacă acea clasă are mai puţine ore în ziua respectivă, decât vreo altă clasă); ar exista o excepţie: cazul când clasa este împărţită în două grupe (una face "Franceză", cealaltă face "Engleză"), apărând atunci într-o aceeaşi coloană la doi profesori – dar în acest caz particular, am folosi desigur două (noi) clase, câte una pentru fiecare dintre cele două grupe (urmând ca orele celor doi profesori la aceste „noi” clase, să fie menţinute în câte o aceeaşi coloană).
Condiţia menţionată trebuie conservată de oricare operaţie (valabilă) efectuată asupra orarului respectiv. Cea mai banală asemenea operaţie constă în schimbarea între ele a două coloane ale orarului (ceea ce în R decurge foarte simplu):
# swap_cols <- function(orz, h1, h2) { # orz[ , c(h1, h2)] <- orz[ , c(h2, h1)] # orz # coloana h1 (h2) a trecut în coloana h2 (h1) # }
Dacă ar fi să folosim mai departe această funcţie, atunci ar trebui să o completăm cu o secvenţă în care să vizăm clasele cu puţine ore: schimbând între ele coloanele 1 şi 5 (de exemplu), clasele care au 4 ore vor începe programul la ora a 2-a din zi şi eventual, trebuie mutate înapoi (iar schimbând coloanele 2 şi 5, clasele cu câte 4 ore trebuie neapărat, mutate înapoi – altfel, clasa ar avea fereastră în ora 2).
Dar schimbarea între ele a două coloane (repetând pentru alte două coloane, ş.a.m.d. – ceea ce este şi uşor de modelat) creşte în general, numărul de ferestre – încât renunţăm să o angajăm mai departe (şi am redat funcţia sub semnul de „comentariu”, '#').
Lanţuri Kempe, în graful lecţiilor din două ore ale zilei
Să desprindem din orar lecţiile repartizate în două coloane oarecare – să zicem, cele corespunzătoare orelor 4 şi 5 ale zilei (ignorând liniile libere, "- -"):
x45 <- MXT[, c(4, 5)] edg <- x45[x45[, 1] != '-' | x45[, 2] != '-', ] colnames(edg) <- c("q1", "q2") > print.table(edg) # pr -4 edg.txt > edg2.txt (redarea textului pe 4 coloane, în Linux)
q1 q2 q1 q2 q1 q2 q1 q2 P26 10D - P33 12A 10A P19 5A 7B P23 11D 9A P29 12C - P50 5C 9E P41 8E 7A P06 9E 12E P10 - 10D P20 10C 5D P12 12D 11D P09 7C 11C P45 - 12C P21 11E - P04 6C 6B P01 6A 8C P62 10B 9D P40 11B 9C P28 12B 10C P25 5D 7E P17 11A 11B P18 7B 6E P32 5E 5A P03 7D 8A P35 - 11A P55 - 12A P37 9A 6C P07 9C 10E P27 5B - P16 10A 5C P08 6D 12D P36 9D 6A P53 7A 6D P42 9B - P22 10E 8E P02 6E 7C P30 6B 5E P34 8B 11E P13 8F 7D P05 12E 10B P15 8D 8B P31 11C 9B P39 8C 8F P43 8A - P11 7E 8D
Nu-i necesar, totuşi putem ignora liniile 1..4 şi 8 („tăiate”, mai sus): schimbarea clasei 10D (şi la fel, pentru 12C) din coloana 'q1' în coloana 'q2' este banală, angajând numai doi profesori; iar clasa 5B are numai 4 ore, deci nu poate fi mutată în ora a 5-a.
Pentru celelalte clase, mutarea dintr-o coloană în cealaltă implică mai mult de două linii (fiindcă fiecare clasă trebuie să apară o singură dată pe coloană). De exemplu, intervertirea orelor profesorului P11 implică 4 linii:
iniţial final q1 q2 q1 q2 P11 7E 8D 8D 7E P15 8D 8B 8B 8D P34 8B 11E 11E 8B P21 11E - - 11E
pe care trebuie înlănţuite intervertirile „elementare” 7E → 8D → 8B → 11E → - (care angajează în serie, o clasă din prima coloană şi una din a doua coloană).
De obicei, problema care se pune nu este intervertirea a două clase la un profesor, ci acoperirea unei ferestre; presupunând că P21 are fereastră în ora a 5-a, acoperirea acesteia se poate obţine intervertind de jos în sus pe cele 4 linii redate mai sus.
Lanţul descris mai sus este în fond, un „lanţ Kempe” (de fapt, doar face parte dintr-un lanţ Kempe); dacă avem un graf ale cărui vârfuri au fost „colorate” (sau etichetate) astfel încât oricare două noduri adiacente să aibă culori diferite, atunci un lanţ maximal al grafului, format numai din noduri colorate cu una dintre două culori 'q1' şi 'q2' date, se numeşte (q1-q2)-lanţ Kempe. Este de observat că lanţul evidenţiat mai sus nu este maximal, putând fi prelungit în capătul '7E' (cu 7E ← 5D ← 10C ← 12B).
Într-un asemenea lanţ, cele două culori alternează (fiindcă vârfurile vecine nu pot să aibă o aceeaşi culoare) şi se pot interverti (fără a afecta graful), fiindcă lanţul este unul maximal. Mai încolo vom sublinia o deosebire între a interverti două clase la un profesor şi a interverti cele două culori într-un lanţ Kempe (deşi semnifică aici un acelaşi efect – „mutarea” dintr-o coloană în alta)…
Să considerăm – folosind iarăşi igraph – graful orientat G care are drept arce perechile ordonate (q1, q2):
require(igraph) G <- graph_from_edgelist(edg[-c(1:4, 8), ]) > G IGRAPH 5dcd6b6 DN-- 39 40 -- # 39 vârfuri, 40 arce + attr: name (v/c) + edges from 5dcd6b6 (vertex names): [1] 10B->9D 11A->11B - ->11A 7A ->6D 6B ->5E 8D ->8B 8A ->- 12A->10A [9] 5C ->9E 10C->5D 11E->- 11B->9C 7B ->6E - ->12A 10A->5C 9B ->- [17] 8B ->11E 11C->9B 7E ->8D 5A ->7B 8E ->7A 12D->11D 6C ->6B 12B->10C [25] 5E ->5A 9A ->6C 6D ->12D 10E->8E 8F ->7D 8C ->8F 11D->9A 9E ->12E [33] 7C ->11C 6A ->8C 5D ->7E 7D ->8A 9C ->10E 9D ->6A 6E ->7C 12E->10B
Un "plot(G)" simplu (fără alţi parametri) ne arată imediat că G conţine trei lanţuri maximale, care pleacă respectiv din '12B', '12A' şi '11A' şi se încheie în '-' (din '12B' avem un lanţ obişnuit (deschis); celelalte două sunt lanţuri închise („cicli”, sau „circuite”)):
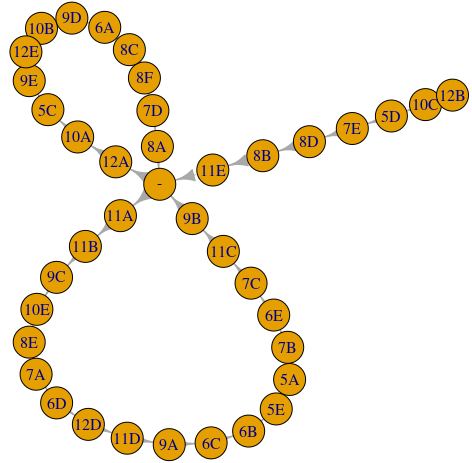
Fiecare lanţ alternează o clasă din coloana 'q1' cu una din 'q2', fiind deci lanţuri Kempe ale grafului G. Putem obţine într-o listă, cele trei lanţuri, folosind all_simple_paths():
Lm <- map(c("11A", "12A", "12B"), function(cls) all_simple_paths(G, from = cls, to = '-', mode="out"))
De exemplu, pentru lanţul care pleacă din '12B' (unde regăsim şi lanţul intervertirilor exemplificate mai sus pentru profesorul 'P11'):
> Lm[[3]][[1]] + 8/39 vertices, named, from accc77e: [1] 12B 10C 5D 7E 8D 8B 11E -
Să colorăm vârfurile lui G în două culori, alternându-le în cadrul fiecărui lanţ; vârful '-' este unul special (reprezintă „fereastră”, sau oră liberă – nu clasă), încât îl marcăm altfel decât celelalte vârfuri. Apoi, să producem o imagine grafică, specificând funcţiei plot.igraph(G, ...) diverşi parametri de reprezentare a vârfurilor şi arcelor, precum şi algoritmul care decide coordonatele poziţionării acestora în pagina grafică:
V(G)[unlist(Lm)]$color <- c("orange", "skyblue") V(G)[V(G)$name == '-']$color <- "yellow" coords <- layout_nicely(G) plot(G, vertex.frame.color=NA, vertex.size=10, vertex.shape = ifelse(V(G)$name == '-', "csquare", "circle"), vertex.label.family="sans", vertex.label.cex=0.8, edge.arrow.size=0.2, edge.arrow.width=2, edge.curved=TRUE, edge.arrow.mode=2, layout = coords)
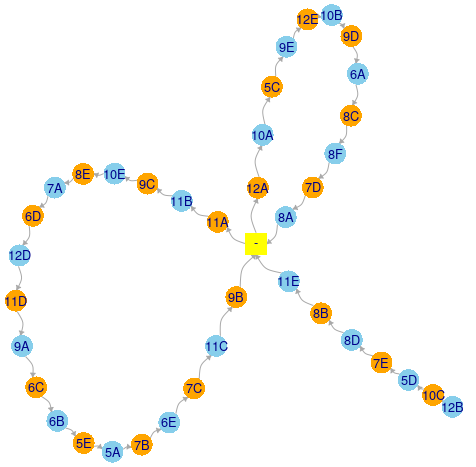
Intervertirea celor două culori pe oricare dintre cele trei lanţuri, asigură schimbarea claselor respective din coloana 'q1' (respectiv, 'q2') în coloana 'q2' (respectiv, 'q1'); dar trebuie să observăm că acţiunea trebuie făcută pe întregul lanţ – altfel, operând astfel numai pe un sub-lanţ, ar rezulta şi vârfuri adiacente cu o aceeaşi culoare; de exemplu, intervertind culorile pe sublanţul "7E → 8D → 8B → 11E" din lanţul Lm[[3]] redat mai sus, nodul '7E' ar căpăta aceeaşi culoare ca nodul '5D' din care este implicat în graful iniţial (ori nodurile adiacente trebuie să aibă culori diferite).
Cu alte cuvinte, avem de distins între „intervertirea de clase” şi „intervertirea de culori”; intervertirea de clase produce totuşi un nou graf (fiindcă se schimbă orientarea unora dintre arcele grafului iniţial), în timp ce intervertirea culorilor pe un lanţ Kempe nu modifică graful iniţial, afectând doar colorarea acestuia.
Modelarea acoperirii unei ferestre
Să considerăm o linie din orar, care conţine clasa 'ql' în coloana 'h1' şi „fereastra” (sau locul liber) '-' în coloana 'h2'. Următoarea funcţie mută 'ql' – dacă se poate – din coloana 'h1' în coloana 'h2', corectând de-a lungul celor două coloane – prin interschimbare – suprapunerile de clase.
Ideea este cât se poate de simplă: considerăm vectorii – „locali” funcţiei – L1 şi L2 corespunzători celor două coloane date; dacă 'ql' nu figurează în ambii vectori, atunci refuzăm mutarea clasei (este cazul unei clase cu puţine ore); altfel, facem mutarea şi (pentru a evita suprapunerea a două clase într-un acelaşi vector) continuăm cu mutări de clase înlănţuite de-a lungul celor doi vectori locali, până când ajungem din nou la '-'.
Să observăm că am putea zice mai simplu: inversăm orientările arcelor pe un sublanţ al unui lanţ Kempe din graful asociat cum am arătat mai sus, celor două coloane. Bineînţeles că în final, returnăm noul orar (corespunzător schimbării orientării unora dintre arcele grafului asociat):
swap_cls <- function(morr, h1, h2, ql) { L1 <- morr[, h1] L2 <- morr[, h2] if(! (ql %in% L2 & ql %in% L1)) return(NULL) i <- which(L1 == ql) ## ;print(morr[i, ]) if(L2[i] != '-') return(NULL) morr[i, c(h1, h2)] <- morr[i, c(h2, h1)] ## ;print(morr[i, ]) while(ql != '-') { j <- which(L2 == ql) ## ;print(morr[j, ]) ql <- L1[j] if(! ql %in% L2) return(NULL) morr[j, c(h1, h2)] <- morr[j, c(h2, h1)] ## ;print(morr[j, ]) } morr # returnează matricea rezultată prin mutarea clasei }
Redăm desfăşurat schimbarea clasei '11E' din ora 4 în ora 5, prin swap_cls():
> mor1 <- swap_cls(MXT, h1=4, h2=5, ql="11E") 1 2 3 4 5 6 7 9E 12E - 11E - - - # mută 11E (din `4` în `5`) 9E 12E - - 11E - - - 5A 5B 8B 11E - - # schimbă 8B (cu 11E) - 5A 5B 11E 8B - - - - 8E 8D 8B 10D - # 8D (cu 8B) - - 8E 8B 8D 10D - - 5E - 7E 8D 7D - # 7E (cu 8D) - 5E - 8D 7E 7D - 12C - - 5D 7E 9B - # 5D (cu 7E) 12C - - 7E 5D 9B - 7B 7A - 10C 5D - - # 10C (cu 5D) 7B 7A - 5D 10C - - 11B - 6A 12B 10C 9C - # încheie la 12B
Evident, mutările succesive implicate în acest exemplu corespund parcurgerii în sens invers a lanţului Kempe care pleacă din nodul '12B', de pe graful arătat mai sus.
Asociind coloanelor indicate în 'h1' şi 'h2' graful G (cum am arătat mai sus, pentru orele 4 şi 5) şi vizualizând graful respectiv, putem sesiza uşor ce intervertiri putem face (cu sau fără swap_cls()). De exemplu, pentru clasele din coloanele 1 şi 2 ale orarului nostru avem acest graf G (acum, cu două componente conexe):
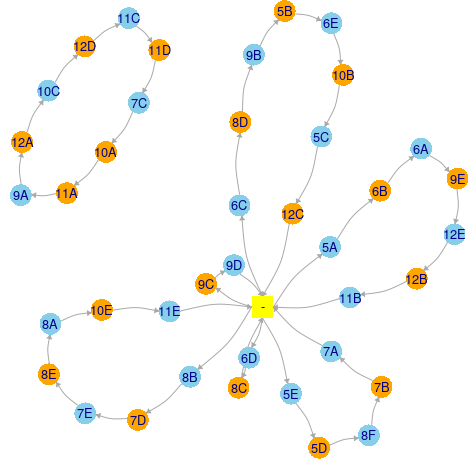
Cele 9 clase de pe circuitul Kempe care nu trece prin '-' pot fi intervertite câte două, pe liniile care le conţin (morr[i, c(1,2)] <- morr[i, c(2,1)], 'i' fiind rangul liniei):
iniţial final `1` `2` `1` `2` P63 11A 9A 9A 11A P71 9A 12A 12A 9A P35 12A 10C 10C 12A P46 10C 12D 12D 10C P60 12D 11C 11C 12D P43 11C 11D 11D 11C P52 11D 7C 7C 11D P14 7C 10A 10A 7C
O asemenea operaţie de intervertire directă (care nu implică swap_cls()) poate fi necesară pentru reducerea ulterioară de ferestre, pe coloanele vecine celor considerate (în cazul de faţă, pe coloana `3`).
Intervertirea culorilor pe un lanţ Kempe care trece prin '-' va comuta fereastra între linia pe care se află clasa care „pleacă” pe lanţul respectiv din '-' şi aceea pe care se află clasa care „ajunge” în '-'; de exemplu, swap(..., ql="11E") va schimba linia "11E -" în "- 11E" şi în final, linia "- 8B" în "8B -" – cum se vede pe grafic pe lanţul care pleacă din '8B' şi ajunge în '11E' (analog, pentru perechile de clase 7A,5E; 11B,5A; etc.).
Văzând grafurile asociate coloanelor 1 şi 2, 2 şi 3, 3 şi 4 (etc.) ale orarului, putem astfel sesiza mai uşor acele intervertiri directe şi operaţii swap(..., ql) care ar conduce împreună, la reducerea numărului de ferestre (e drept însă, că acest „văzând” ţine deocamdată tot de interactiv).
vezi Cărţile mele (de programare)