Pătratul și radicalul unui punct

Ei lasă!… unui punct, nu unui număr?!
În [2] avem această formulare, lipsită de emfază: radicalul unui cerc care trece prin origine este o lemniscată Bernoulli — pentru care este de căpeténie lecția: expresia "radicalul unui cerc" nu există in limbaj curent. Am zis-o fără emfază, fiindcă rezultatul respectiv atinge frumos ceva de pare binecunoscut (urme de prin "teoria funcțiilor complexe"), iar "demonstrația" de data aceasta este banală (păi… nu punem "Definiție", "Teoremă" și "Demonstrație" pentru orice)

Pentru "punct" $P$ (al unei curbe) avem totuși trei interpretări (echivalente): raportând la un sistem de coordonate carteziene, $\boldsymbol{P(x,\,y)}$ (cu $x,\,y\in \mathbb{R}$); raportând la un sistem de coordonate polare, $\boldsymbol{P(r,\,\theta)}$ (cu $r\gt 0$, $\theta\in[0,\,2\pi]$ și cu $x=r\cos \theta$ și $y=r\sin \theta$); iar în planul complex, $\boldsymbol{P(z)}$ (cu $z=x+i\,y = r\,\mathrm{e}^{i\,\theta}\in \mathbb{C}$).
Bineînțeles că, "văzut" astfel, punctul ajunge dependent de alegerea făcută în prealabil pentru originea sistemului de coordonate… Dar dacă este cazul, avem în fiecare caz, formule de trecere a coordonatelor la vreo altă origine.

Fiindcă punctul poate fi văzut iată, ca număr complex, putem vorbi (în mod firesc) de pătrate sau de radicali; pătratul punctului $P(z)$ este punctul $P(z^2)$, sau altfel spus, pătratul punctului $P(r,\,\theta)$ este punctul $P(r^2,\,2 \theta)$; la fel, radicalul punctului $P(r,\,\theta)$ este punctul $P(\sqrt{r\,},\,\theta/2)$ (…împreună cu punctul opus $P(-\sqrt{r\,},\,\theta/2)$).
Dacă $P$ se află pe cercul-unitate, atunci "pătratul" său $P^2$, "radicalul" său $\sqrt{P\,}$ (care, atenție, determină precis două puncte) și mai general, "puterea-n" $P^n$ sunt și ele pe cercul-unitate, unghiurile polare fiind respectiv $\theta$, $2\theta$, $\theta/2$ și $n\theta$ (modulo $2\pi$).
Iar mai general, "produsul punctelor" $(r_1,\,\theta_1)$ și $(r_2,\,\theta_2)$ este punctul $(r_1r_2,\,\theta_1+\theta_2)$…

Avem mai sus nu ceva de marcat pompos ca "Definiție", ci observații elementare care se cade să fie asupra lucrurilor de care avem de vorbit prin lecțiile de "coordonate polare" și de "numere complexe".

Mai trebuie subliniat preventiv, următorul aspect: operațiile cu puncte "definite" mai sus (de exemplu, "opusul" unui punct, sau $P^n$) sunt valabile numai dacă le înrădăcinăm la o aceeași origine (întâlnim situații — v. și în [2], §3.1 — în care este ușor să exprimăm un anumit punct față de o altă origine; atunci, pentru a putea opera cu puncte în contextul respectiv, devine necesar ca în prealabil să transformăm coordonatele de la o origine la cealaltă — situație analogă celeia întâlnite deja la aritmetică, unde aveam de lucrat în mai multe sisteme de numerație; ba chiar și în alte culturi: unii măsoară în kilometri și grade Celsius, alții în mile și grade Fahrenheit).

Iar acest aspect este esențial: nu are sens să vorbim de "pătratul curbei" cutare — adică locul pătratelor punctelor sale — decât dacă adăugăm "față de polul cutare" (pătratul unui cerc față de centrul acestuia este un cerc, dar pătratul lui față de un punct diferit de centru, nu mai este un cerc!)

Pătratul unei curbe Cassini (…este un cerc?);
radicalul unui cerc este o anumită curbă Cassini

O curbă Cassini (de parametri $a, b$) este formată din punctele ale căror coordonate polare $(\boldsymbol{r},\,\boldsymbol{\theta})$ satisfac ecuația (v. [3]):

Este de subliniat că această ecuație ține în mod implicit de sistemul de coordonate constituit de axele de simetrie ale curbei respective (altfel, ea trebuie "rotită" și apoi "translatată" la originea existentă).

Cu un mic "truc" elementar, (1) se poate rescrie imediat astfel:

ceea ce exprimă pătratul distanței dintre punctele $H(\boldsymbol{r^2\cos 2\theta},\,\boldsymbol{r^2\sin 2\theta)}$ — de fapt, în coordonate polare, $H\boldsymbol{(r^2,\,2\theta)}$ — și $K(\boldsymbol{a^2},\,\boldsymbol{0})$; prin urmare, pentru orice $r$ și $\theta$, avem $\boldsymbol{\mathrm{dist}}(H, K)=\boldsymbol{b^2}$. Dar $K$ este un punct fix — anume, pătratul focarelor lui $\Gamma$, $\pm\,(a,\,0)$ — iar $H$ este pătratul unui punct oarecare $\boldsymbol{(r,\,\theta)}$ al curbei (1); rezultă:

Teoremă. 1. Pătratul unei curbe Cassini $\Gamma(a, b)$ — față de centrul acesteia — este un cerc de rază $b^2$, cu centrul în punctul corespunzător pătratului față de centrul lui $\Gamma$, al focarelor.
2. (invers) Radicalul unui cerc de rază $b^2$, cu centrul în punctul de afix $z_0$ este curba Cassini de parametri $a,\,b$ cu $a=|\,\sqrt{z_0\,}\,|$. În particular (v. și [2]): radicalul unui cerc care trece prin origine este o lemniscată Bernoulli.

De observat că în formularea "inversă", $\Gamma$ nu mai este referită la axele proprii; redăm grafic situațiile caracteristice — schițând numai $\Gamma$ și cercul din care provine, marcând doar axa polară, originea ei și vectorii de poziție ai centrului și focarelor:

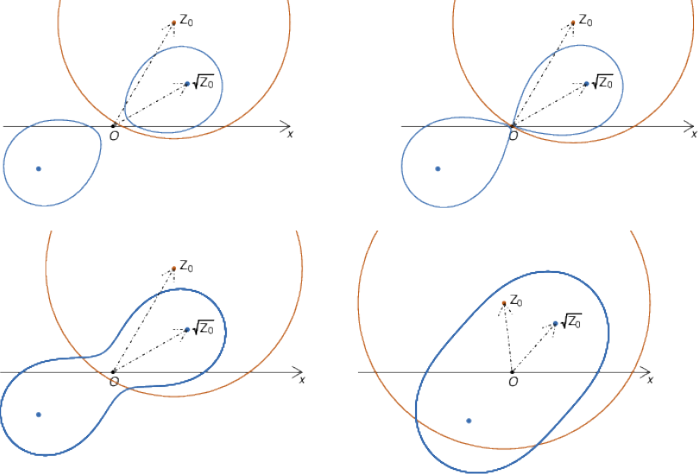
Fig.1 Transformarea cercului în oval Cassini

Figura a fost produsă experimentând (cu un program pe care îl omitem aici) cu valori mici pentru centrul și raza cercului; oricum ar fi (ca "reușită"), ea ne-ar spune că forma curbei $\Gamma$ rezultate ca "radicalul cercului", depinde de poziția față de polul $O$: dacă $O$ este exterior cercului, atunci $\Gamma$ este formată din două ovale convexe disjuncte (cazul $b\lt a$, v. [3]-II); dacă $O$ se află pe cerc, $\Gamma$ este o lemniscată Bernoulli ($a=b$); iar dacă $O$ este interior cercului, atunci $\Gamma$ este un oval Cassini obișnuit (cazurile $a \lt b \lt a\sqrt{2\,}$ și $b \ge a\sqrt{2\,}$, reprezentate respectiv pe al doilea rând al figurii).

Cercul din care provine prin radical, o curbă Cassini dată

Mai sus am plecat de la un cerc oarecare și aplicându-i radicalul (față de polul la care referisem și cercul), am obținut o curbă Cassini. Cealaltă variantă, când plecăm de la o curbă $\Gamma$ oarecare și vrem să determinăm cercul al cărui radical (față de un anumit pol) coincide cu $\Gamma$, are o discuție mai complicată.

Mai întâi, să vedem cum trasăm o curbă $\Gamma$ cu focarele $G$, $H$ și parametrul $b^2$ date arbitrar. Fiindcă $a=\textrm{dist}(G,\,H)\,/\,2$, putem scrie ecuația algebrică a curbei Cassini $\Gamma_1$ raportate la axele proprii (v. eventual, [3]); apoi, pentru a obține din ecuația lui $\Gamma_1$ pe aceea a lui $\Gamma$, trebuie să rotim sistemul $xOy$ cu unghiul dintre axa $Ox$ și dreapta focarelor $GH$, după care să translatăm originea $O$ în mijlocul segmentului $GH$.

Dar este mai simplu să folosim direct definiția ovalelor Cassini:

cassinian <- function(x, y)
    # produsul distanțelor la focarele (fx,fy) și (gx,gy) este b^2
    ((x-fx)^2 + (y-fy)^2) * ((x-gx)^2 + (y-gy)^2) - b^4

Specificăm focarele și $b$, apoi constituim conturul lui $\Gamma$, folosind funcția cassinian():

# focarele H = 1+2i și G = 3-2i
fx <- 1; fy <- 2;  H <- fx + 1i*fy
gx <- 3; gy <- -2;  G <- gx + 1i*gy
b <- 2.2
# punctele cassinienei de focare H, G și parametru b^2
X <- seq(-1, 5, by=0.01)
Y <- seq(-3, 5, by=0.01)
Z <- outer(X, Y, cassinian)
V <- contourLines(X, Y, Z, levels = 0) [[1]]

contourLines nu plotează graficul (spre deosebire de contour(), folosită în [3]), ci reurnează o matrice conținând (aici) cam 1000 de puncte $(x,y)$ care (datorită intermedierii prin outer()) satisfac ecuația din cassinian() (și sunt suficiente puncte, sau segmente, pentru a desena apoi cu suficientă acuratețe, conturul lui $\Gamma$).

Cu $a,\,b$ rezultați mai sus, $\Gamma$ este formată din două ovale disjuncte; pentru a le produce (după ce inițializăm fereastra grafică, v. [3]-I), putem proceda cam așa:

W <- V$x + 1i*V$y
points(W, type="l", asp=1, lwd=1.5)  # trasează... primul oval (NU ambele!)
mj <- (H + G) / 2  # centrul cassinienei
W2 <- 2*mj - W  # simetrizează față de centru, pentru al doilea oval
points(W2, type="l", asp=1, lwd=1.5)
# Acum ridică la pătrat, dar... greșit!
points(W^2, col="blue", type="l", lwd=0.6)  # pătratul, dar... față de cine?
points(W2^2, col="blue", type="l", lwd=0.6)

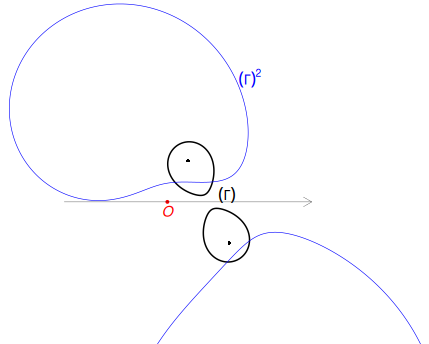
Fig.2 $\boldsymbol{(\Gamma)^2}$ față de un pol $O$ nepotrivit, nu este un cerc

După ce am trasat $\Gamma$, am ridicat fără nicio grijă la pătrat, așteptând (chipurile, conform teoremei formulate mai sus) ca $\Gamma^2$ să fie cercul din care prin radical rezultă înapoi, $\Gamma$; dar curba albastră care ne-a rezultat este foarte departe de a fi un cerc…
Teorema precizează totuși că "pătratul" trebuie referit la centrul lui $\Gamma$, ori în Fig.2 pătratul a fost calculat față de originea inițială $O$.

Conform teoremei, centrul cercului este pătratul focarelor lui $\Gamma$, pătratul trebuind calculat față de centrul lui $\Gamma$; altfel spus, centrul cercului este în punctul $(H-mj)^2$:

s <- seq(0, 2*pi, length=1000)
K <- (H-mj)^2 + b^2*exp(1i*s)
points(K, type="l", lty=2, col="blue")

Acum, $\sqrt{K\,}$ (cu radical față de polul $O$) dă curba $\Gamma$, dar nu în poziția corectă: curba roșie rezultată (v. mai jos imaginea din stânga) nu se suprapune peste $\Gamma$ trasată cu negru. Deci trebuie ca în final să translatăm $\sqrt{K\,}$ cu vectorul $mj$ — și atunci obținem (în dreapta) figura corectă, în care "radicalul" translatat al cercului se suprapune lui $\Gamma$ (care din negru, devine roșu):

points(sqrt(K) + mj, col="red", cex=0.1)
points(-sqrt(K) + mj, col="red", cex=0.1)

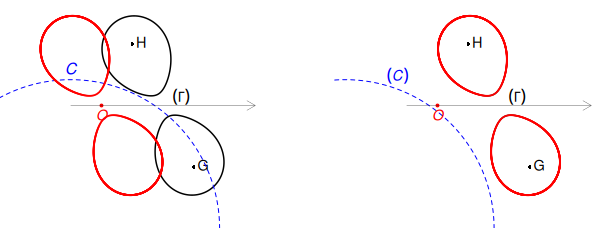
Fig.3 $(\Gamma)$ și pătratul său $(C)$ (dar cercul trebuie dedus corect din $\Gamma$)
stânga: aproape corect: mai trebuie o translație, pentru a avea $\sqrt{(C)}=(\Gamma)$
dreapta: corect, $\sqrt{(C)}$ coincide cu $(\Gamma)$

Poate că în loc de "radicalul cercului" ar trebui să zicem "radicalul translatat"… Oricum teorema este acum (sau pare a fi) complet clarificată; ar mai fi poate de văzut dacă există și un alt cerc, care prin "radical translatat" se transformă într-o curbă Cassini dată în prealabil (se poate vedea că totuși, cercul din stânga nu este același, cu cel "corect" din dreapta!).

Iar despre alte "Puterile cercului" am mai discutat (prin 2018), stabilind de exemplu că față de un punct al său, pătratul este o cardioidă, iar cubul său este o sextică Cayley…
(vreun filosof inspirat ar zice că până la urmă, toate se nasc dintr-un cerc!)