Puterile cercului, faţă de un punct al său (partea a II-a)
 Considerăm un cerc $\mathcal{C}$ şi sistemul de coordonate polare cu originea $\mathsf{O}$ într-un punct fixat al cercului şi cu axa polară $\mathsf{O}x$ peste diametrul prin $\mathsf{O}$ al cercului; luăm ca unitate de măsură diametrul cercului (astfel vom avea o simplificare foarte convenabilă faţă de [1], unde luam ca unitate chiar raza cercului).
Considerăm un cerc $\mathcal{C}$ şi sistemul de coordonate polare cu originea $\mathsf{O}$ într-un punct fixat al cercului şi cu axa polară $\mathsf{O}x$ peste diametrul prin $\mathsf{O}$ al cercului; luăm ca unitate de măsură diametrul cercului (astfel vom avea o simplificare foarte convenabilă faţă de [1], unde luam ca unitate chiar raza cercului).
Ecuaţia polară a lui $\mathcal{C}$ este $\rho=\cos\theta$ (faţă de [1], "am scăpat" de factorul 2). Coordonatele carteziene $x=\rho\cos\theta=\cos^2\theta$ şi $y=\rho\sin\theta=\frac{1}{2}\sin 2\theta$ îşi repetă valorile cu periodicitatea $\pi$, încât dacă vrem ca $\mathcal{C}$ să fie parcurs o singură dată, trebuie să limităm valorile $\theta$ la un interval de lungime $\pi$; vom considera $\theta\in[0,\,\pi]$ (astfel, cercul va fi parcurs în sens antiorar începând din punctul (1,0); pentru a-l parcurge începând din $\mathsf{O}$, am putea considera $\theta\in[-\pi/2,\,\pi/2]$).
Prin scalarea (variabilă) cu factorul $\rho^n$ urmată de rotirea cu $n\theta$ se obţin punctele curbei $\mathcal{C}^n$ - "puterea $n$" a lui $\mathcal{C}$; vom considera cazul cel mai simplu, când $n$ este număr natural nenul.
Ecuaţia lui $\mathcal{C}^n$ este (în planul complex raportat la $\mathsf{O}$ ca origine şi cu axa reală peste axa polară $\mathsf{O}x$, exprimând punctele cercului unitate prin formula lui Euler $\mathsf{e}^{\theta i}=\cos\theta+i\sin\theta$): $$z_n(\theta)=\,\mathsf{e}^{n\theta i}\cos^n \theta,\;\theta\in[0,\pi]\quad\quad\quad\small(1)$$
Obs. Poate fi utilă şi o altă exprimare: punctele lui $\mathcal{C}$ sunt $\cos^2\theta+\frac{1}{2}i\sin 2\theta=$ $=\frac{1}{2}(\cos 2\theta+i\sin 2\theta+1)=\frac{1}{2}(\mathsf{e}^{2\theta i}+1)$, deci pentru $\mathcal{C}^n$ avem $z_n(\theta)=\frac{1}{2^n}(\mathsf{e}^{2\theta i}+1)^n$.
Avem o relaţie de recurenţă evidentă, pe care o vom putea folosi în programe pentru a obţine vectorul punctelor lui $\mathcal{C}^{n+1}$ din vectorul existent al punctelor lui $\mathcal{C}^n$ (fără a repeta calculul (1)): $$z_{n+1}(\theta)=z_n(\theta)\,\mathsf{e}^{\theta i}\cos\theta\quad\quad\quad\small(2)$$
Toate curbele $\mathcal{C}^n$ sunt cuprinse în discul unitar şi au punctul $(1,0)$ ca vârf comun (spre deosebire - cu dezavantajul că acum vârful este comun - faţă de [1], unde aveam de multiplicat cu $2^n$).
Valorile (1) pentru $\theta$ şi respectiv $(\pi-\theta)$ sunt numere complexe conjugate; deci arcul din $\mathcal{C}^n$ parcurs cu $\theta$ de la $0$ la $\pi/2$ (începând din punctul $(1,0)$ şi buclând spre $\mathsf{O}$) este simetric faţă de $\mathsf{O}x$ celui parcurs (începând din $\mathsf{O}$ şi continuând spre $(1,0)$) când $\theta$ variază între $\pi/2$ şi $\pi$.
Să notăm prin $\mathsf{P}^n_\theta$ punctul lui $\mathcal{C}^n$ corespunzător prin (1) unei valori $\theta\in(0,\,\pi/2)$.
Figura următoare ilustrează unele proprietăţi prezentate mai jos, redând $\mathcal{C}^n$ şi $\mathsf{P}^n_\theta$ pentru $n=1..4$ (asociind câte o culoare distinctă, în loc de etichete) şi cu $\theta=\pi/5$:
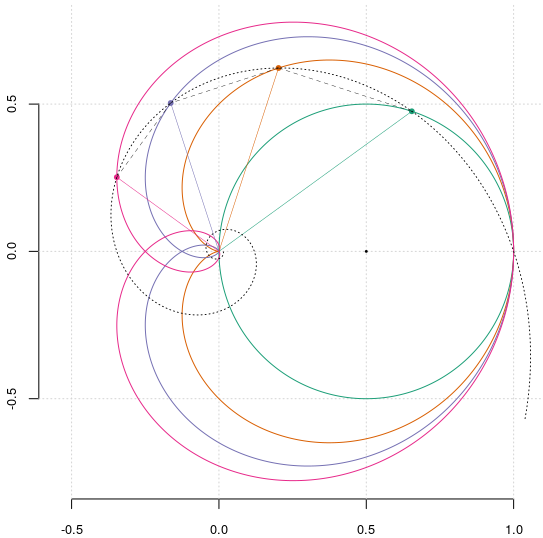
Avem $\mathsf{OP}^{n+1}_\theta\perp\mathsf{P}^n_\theta\mathsf{P}^{n+1}_\theta$ (fiindcă $\mathsf{OP}^{n+1}_\theta=\mathsf{OP}^n_\theta\cos\theta$ exprimă tocmai condiţia ca $\mathsf{OP}^{n+1}_\theta$ să fie proiecţia ortogonală a segmentului $\mathsf{OP}^n_\theta$ pe dreapta care trece prin $\mathsf{O}$ şi face unghiul $\theta$ cu $\mathsf{OP}^n_\theta$).
Rezultă şi că pentru un acelaşi $\theta$, toate triunghiurile $\mathsf{OP}^n_\theta\mathsf{P}^{n+1}_\theta$ sunt triunghiuri dreptunghice asemenea între ele (unghiurile lor din $\mathsf{O}$ fiind egale cu $\theta$).
Mai mult, $\mathsf{P}^n_\theta\mathsf{P}^{n+1}_\theta$ este tangentă în $\mathsf{P}^n_\theta$ curbei $\mathcal{C}^n$. Într-adevăr, diferenţa ordonatelor punctelor $\mathsf{P}^{n+1}_\theta$ şi $\mathsf{P}^n_\theta$ este $\small\cos^n\theta\left(\cos\theta\sin(n+1)\theta-\sin n\theta\right)=\cos^n\theta\left(\frac{1}{2}\sin(n+2)\theta-\frac{1}{2}\sin n\theta\right)=$ $=\small\cos^n\theta\sin 2\theta\cos(n+1)\theta$, iar diferenţa absciselor este $\small-\cos^n\theta\sin 2\theta\sin(n+1)\theta$; rezultă că panta dreptei respective este $-\mathrm{ctg}\,(n+1)\theta$.
Pe de altă parte, aceeaşi pantă găsim pentru tangenta în $\mathsf{P}^n_\theta$ la $\mathcal{C}^n$: $\frac{\mathsf{d}y/\mathsf{d}\theta}{\mathsf{d}x/\mathsf{d}\theta}=\frac{(\cos^n\theta\sin n\theta)'}{(\cos^n\theta\cos n\theta)'}=$ $\frac{\sin n\theta\sin\theta-\cos\theta\cos n\theta}{\cos n\theta\sin\theta+\cos\theta\sin n\theta}=\frac{-\cos(n+1)\theta}{\sin(n+1)\theta}=-\mathrm{ctg}\,(n+1)\theta$.
Rezultă (variind $\theta$) această proprietate: $\mathcal{C}^{n+1}$ este podara lui $\mathcal{C}^n$ faţă de $\mathsf{O}$ (locul picioarelor perpendicularelor din $\mathsf{O}$ pe tangentele lui $\mathcal{C}^n$).
Obs. În [1] (singura diferenţă fiind considerarea razei şi nu a diametrului, ca unitate) $\mathcal{C}^{n+1}$ era orthotomica lui $\mathcal{C}^n$ faţă de $\mathsf{O}$ (iar $\mathsf{OP}^n_\theta\mathsf{P}^{n+1}_\theta$ erau triunghiuri isoscele asemenea).
Obs. Cercul cu diametrul $\mathsf{OP}^n_\theta$ este tangent în $\mathsf{P}^{n+1}_\theta$ la $\mathcal{C}^{n+1}$. Aceasta rezultă calculând ca mai sus (făcând diferenţa ordonatelor, etc.) panta dreptei care uneşte $\mathsf{P}^{n+1}_\theta$ cu mijlocul segmentului $\mathsf{OP}^n_\theta$; se obţine $\mathsf{tg}\,(n+2)\theta$ - deci invers şi de semn contrar cu panta tangentei în $\mathsf{P}^{n+1}_\theta$ la $\mathcal{C}^{n+1}$, astfel că dreapta menţionată este normala în $\mathsf{P}^{n+1}_\theta$ la $\mathcal{C}^{n+1}$ şi în acelaşi timp, ea este normala în $\mathsf{P}^{n+1}_\theta$ la cercul de diametru $\mathsf{OP}^n_\theta$ (dat fiind că aşa cum am arătat mai sus, triunghiul $\mathsf{OP}^n_\theta\mathsf{P}^{n+1}_\theta$ este dreptunghic în $\mathsf{P}^{n+1}_\theta$).
Dar precizăm că această proprietate este valabilă în general: podara faţă de un punct fixat al unei curbe este înfăşurătoarea cercurilor care au ca diametri segmentele care unesc punctul fixat cu punctele curbei date (v. Pedal).
Pentru o valoare $\theta$ fixată, punctele $\mathsf{P}^n_\theta$ sunt situate (justificând ca în [1]) pe spirala (trasată cu linie punctată, în figura de mai sus) $z_{\theta}(t)=(\cos\theta)^{t/\theta}\mathsf{e}^{it},\,t\in\mathbb{R^*}$; vom vedea mai jos că $\mathcal{C}^n$ (începând de pe la $n=5$) se comportă ea însăşi ca o spirală, în jurul originii.
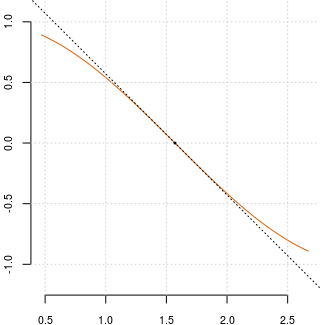 Bineînţeles că pentru studierea unei funcţii ne servim şi de programe într-un limbaj sau altul, pentru a-i percepe mai bine sau a-i valida cumva, comportamentul; dar nu trebuie să uităm că în programe avem de-a face cu aproximări şi uneori, comportarea în jurul anumitor puncte este chiar greu de redat grafic.
Bineînţeles că pentru studierea unei funcţii ne servim şi de programe într-un limbaj sau altul, pentru a-i percepe mai bine sau a-i valida cumva, comportamentul; dar nu trebuie să uităm că în programe avem de-a face cu aproximări şi uneori, comportarea în jurul anumitor puncte este chiar greu de redat grafic.
De exemplu, alăturat avem graficul $y=\cos x$ pe intervalul $\small\pi/2\pm 0.3$ şi vedem că el aproape coincide, cu o anumită porţiune din dreapta care îi este de fapt doar tangentă (în punctul $(\pi/2,0)$); cele două porţiuni se disting între ele doar fiindcă am folosit culori şi stiluri de linie diferite.
Obs. Precizăm că se pot folosi facilităţile browser-ului (click-dreapta şi "View Image"), pentru a vedea imaginile la dimensiunea originală.
Pe următorul panou avem graficele $\mathcal{C}^n$ pentru $n=5,\,6,\,9,\,23$ (cu un program R ca în [1]):
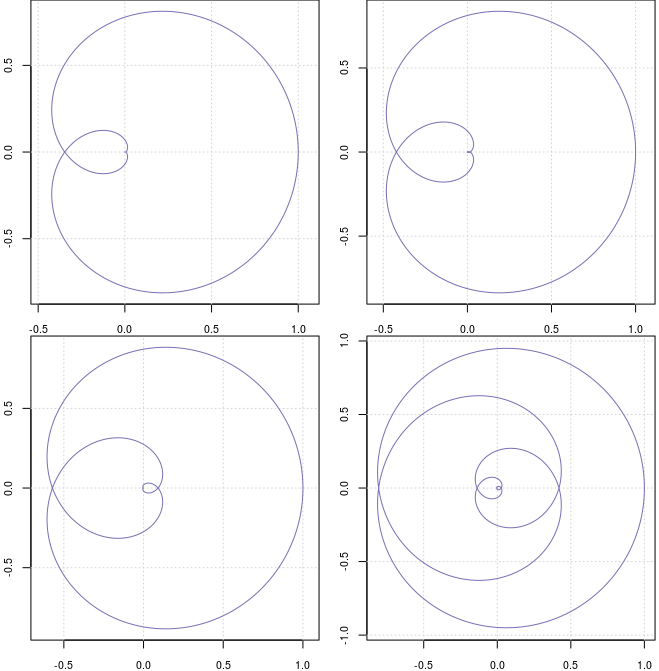
Porţiunea din jurul originii (punct care corespunde valorii $\theta=\pi/2$) este greu de distins; încercăm să analizăm sau să descriem $\mathcal{C}^n$ în jurul punctului $\mathsf{O}$, plecând de la intersecţiile cu axele.
Pentru punctele (1) aflate pe axa reală trebuie să avem $z_n(\theta)=\overline{z_n(\theta)}$; rezultă $\theta=\pi/2$ (de la $\cos^n \theta=0$), sau $\theta=k\pi/n,\,k=0..n$ (din $\mathsf{e}^{n\theta i}=\mathsf{e}^{-n\theta i}$). Dar ne interesează punctele ca atare (nu şi de câte ori trece curba prin acestea), astfel că avem de socotit numai cazurile $\theta\in[0,\pi/2]$; rezultă că $\mathcal{C}^n$ are pe axa reală $[\frac{n}{2}]+1$ puncte, cu abscisele $(-1)^k\cos^n k\frac{\pi}{n},\,k=0..[\frac{n}{2}]$, plus în cazul când $n$ este impar, punctul $\mathsf{O}$ (care pentru $n$ par, se regăseşte la $k=n/2$).
Pe axa imaginară sunt punctele (1) pentru care $z_n(\theta)=-\overline{z_n(\theta)}$, deci acelea obţinute pentru $\theta=(2k-1)\frac{\pi}{2n},\,k=1..n$, plus în cazul când $n$ este par $\theta=\pi/2$.
Obs. Pentru a furniza intersecţiile cu axele nu este nevoie de paritatea lui $n$: punctul $\mathsf{O}$ va apărea între cele indicate de $k$ (apărând pe axa reală dacă $n$ este par, respectiv pe cea imaginară dacă $n$ este impar).
Mărind $n$, rezultă intersecţii cu axele din ce în ce mai apropiate de $\mathsf{O}$; pentru a le reda împreună cumva cu traseul parcurs, am folosit acest artificiu: am ridicat abscisele şi ordonatele punctelor la puterea $1/n$ (ceea ce măreşte suficient de mult valorile iniţiale - păstrându-le totuşi în discul unitar - dat fiind că acestea sunt subunitare); desigur, obţinem astfel doar un soi de "diagramă" formală pentru traseul parcurs pe $\mathcal{C}^n$ - dar (cum vom arăta mai jos) ea sugerează suficient de bine (până pe la $n=40$) modul în care $\mathcal{C}^n$ buclează în jurul originii.
Mai precis, ne-am folosit de următorul program R, în care funcţia $\mathsf{Cn()}$ furnizează un vector de puncte ale lui $\mathcal{C}^n$, funcţia $\mathsf{Qn()}$ modifică punctele lui $\mathcal{C}^n$ considerând valorile radicalilor de ordinul $n$ ale coordonatelor acestora, iar funcţia $\mathsf{cutxy()}$ găseşte intersecţiile lui $\mathcal{C}^n$ cu axele, plotează punctele corespunzătoare acestora prin mărirea de coordonate prevăzută la $\mathsf{Qn()}$ şi le etichetează (specificând un număr de zecimale suficient) cu valorile iniţiale:
Cn <- function(k, th=NULL, from=0, to=pi) { if(is.null(th)) th <- seq(from, to, by=0.0001) cos(th)^k * exp(1i*k*th) } Qn <- function(k, th=NULL, from=0, to=pi) { if(is.null(th)) th <- seq(from, to, by=0.0001) x <- cos(th)^k * cos(k*th) y <- cos(th)^k * sin(k*th) sign(x)*abs(x)^(1/k) + 1i*sign(y)*abs(y)^(1/k) } cutxy <- function(n) { tx <- seq(0, n, by=1)*pi/n ty <- seq(1, 2*n-1, by=2)*pi/(2*n) zx <- Re(Cn(n, tx)); # print(sprintf("%.10f", zx)) x <- sign(zx)*abs(zx)^(1/n) zy <- Im(Cn(n, ty)); # print(sprintf("%.10f", zy)) y <- sign(zy)*abs(zy)^(1/n) points(x+0i, pch=20, cex=0.4) points(1i*y, pch=20, cex=0.6) epsilon <- .Machine$double.eps # 2.220446e-16 y <- y[abs(y) > epsilon] text(1i*y, labels=sprintf("%.8f", zy[abs(zy) > epsilon]), pos=4, cex=0.8) x <- x[abs(x) > epsilon] text(x+0i, labels=sprintf("%.8f", zx[abs(zx) > epsilon]), cex=0.7, srt=45) } op <- par(mfrow = c(2, 2), mar = c(1, 1, 0, 0)) for(n in c(6,7)) { plot(Qn(n), type="n", xlab="", ylab="", xaxt="n", yaxt="n", bty="n") cutxy(n) points(Qn(n, to=pi/2), type="l", col=kol[3]) points(Qn(n, from=pi/2), type="l", lty="dotted", col="red", lwd=1.3) plot(Cn(n), type="n", xlab="", ylab="", xaxt="n", yaxt="n", bty="n", asp=1); grid() points(Cn(n, to=pi/2), type="l", col="#7570B3") points(Cn(n, from=pi/2), type="l", lty="dotted", col="red") } par(op)
În finalul programului, am asamblat într-un panou grafic pentru două valori $n$ indicate direct, "diagrama" traseului (adică graficul lui $\mathsf{Qn()}$ împreună cu specificaţia intersecţiilor cu axele) şi alături, graficul real al curbei $\mathcal{C}^n$; de exemplu, pentru $n=3$ şi $n=4$ obţinem:

Arcele parcurse cu $\theta\in[0,\pi/2]$ ("primul") şi respectiv, $\theta\in[\pi/2,\pi]$ ("al doilea" arc) au fost marcate folosind culori şi tipuri de linie distincte.
Pe prima diagramă citim că traseul $\mathcal{C}^3$ pleacă din punctul $(1,0)$ "în sus şi spre stânga", taie $\mathsf{O}y$ în punctul de ordonată $\approx 0.65$, merge spre stânga şi în jos, intersectând $\mathsf{O}x$ la abscisa $-0.125$, apoi continuă în jos şi spre dreapta până în $\mathsf{O}$ - încheind primul arc; al doilea arc (punctat) pleacă din $\mathsf{O}$ spre stânga şi (uşor) în sus, trece prin intersecţia cu $\mathsf{O}x$ a primul arc, coboară şi merge spre dreapta în mod simetric primului arc, încheind în punctul $(1,0)$.
$\mathcal{C}^2$ (o cardioidă) şi $\mathcal{C}^3$ (o sextică Cayley) sunt cazuri "fără probleme"; dar pentru $n\ge 4$, în $\mathsf{O}$ se formează mici "adâncituri" şi bucle. Astfel, pentru $n=4$ a doua diagramă din panoul de mai sus arată că primul arc, după ce taie $\mathsf{O}x$ la abscisa $-0.25$, continuă dedesubt şi spre dreapta dar nu ajunge direct în $\mathsf{O}$, ci întâi taie $\mathsf{O}y$ la ordonata $\approx -0.0214$ şi apoi curbează (rămânând dedesubtul axei $\mathsf{O}x$) spre $\mathsf{O}$ (care este capătul final pentru "primul arc"); adâncitura creată astfel în $\mathsf{O}$ este deja greu de distins pe graficul lui $\mathsf{C}^4$ (alăturat diagramei).
Începând de la $n=5$, $\mathcal{C}^n$ "buclează" în jurul originii, adică "primul arc" taie $\mathsf{O}y$ la o anumită ordonată negativă, continuă spre dreapta şi în sus, taie $\mathsf{O}x$ la o anumită abscisă pozitivă (din ce în ce mai mică) şi se curbează spre $\mathsf{O}$ pe deasupra axei orizontale:

Pentru $n=5$ (prima diagramă de mai sus) am avea o "buclă simplă" în $\mathsf{O}$: după ce taie $\mathsf{O}x$ (la abscisa $\approx 0.0028$) primul arc curbează direct spre $\mathsf{O}$ (fără a tăia în alt punct, axa verticală). Începând însă cu $n=6$ (a doua diagramă), am avea un alt tip de buclă: primul arc taie $\mathsf{O}y$ la $-0.125$, urcă şi întâlneşte $\mathsf{O}x$ la abscisa $\approx 0.0156$, apoi urcă spre stânga şi taie din nou $\mathsf{O}y$, la ordonata $\approx 0.0003$ şi apoi curbează prin stânga axei verticale spre $\mathsf{O}$ (direct spre $\mathsf{O}$, fără a tăia o a doua oară $\mathsf{O}x$); arcul al doilea "întregeşte" simetric bucla, sau buclele respective.
Începând de la $n=7$ apar şi intersecţii cu $\mathsf{O}x$ în stânga originii, de exemplu pentru $n=12$ obţinem diagrama următoare:

Valorile ordonatelor sau absciselor intersecţiilor cu axele din jurul originii devin aşa de mici (pe diagrama tocmai redată avem ordonata $0.00000000002$) încât dacă vrem să le redăm pe diagramă atunci trebuie să mărim în program, numărul de zecimale prevăzut pentru afişare (iar pe graficul lui $\mathcal{C}^n$ porţiunea respectivă chiar nu mai poate fi redată prin pixeli distincţi).
Pentru valori mai mari ale lui $n$ (dacă vrem să continuăm astfel investigaţia), chiar eliminăm din program secţiunea de etichetare a intersecţiilor; de exemplu pentru $n=40$:
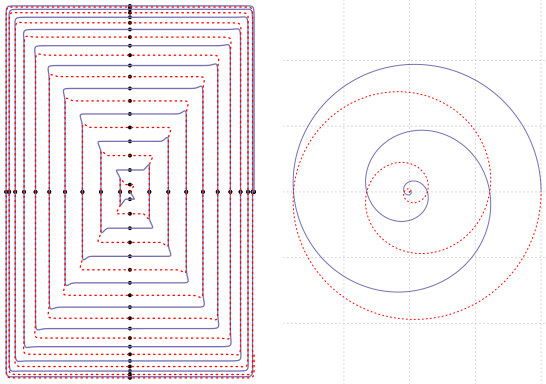
Validăm astfel că $\mathcal{C}^n$ arată (sau se comportă) ca o spirală închisă, formând în jurul originii un anumit număr de spire sau "bucle" (care s-ar putea socoti după numărul de intersecţii cu $\mathsf{O}x$); buclele cel mai apropiate de origine sunt din ce în ce mai mici, pe măsură ce $n$ creşte (şi practic, ele nu mai pot fi redate grafic, decât eventual prin "diagrame" de genul celor imaginate mai sus).
vezi Cărţile mele (de programare)