Am preluat oral tocmai din Paris (v. WatsApp), următoarea problemă elementară:

a se demonstra că suprafațele haşurate sunt egale:

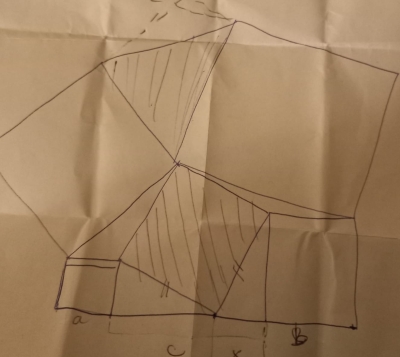
S-a ivit astfel un prilej fericit (după cele 4 luni în care am lucrat numai la cartea [1]), de a revedea ceva geometrie și ceva MetaPost…

N-am găsit vreo referință oficială (că asta am încercat întâi), așa că am abordat problema în două trepte: mai întâi într-un caz particular relevant (prezentat mai jos); apoi după o anumită iluminare târzie, pe „cazul general”.

Două cazuri particulare

Și pentru cazuri particulare, poate fi vorba de ceva „inspirație” (dar aceasta apare de obicei „după”…); pe următoarea particularizare extremă a figurii de mai sus, devine evident că părțile hașurate au aceeași arie:

Desigur, am creat figura folosind MetaPost: am plecat de la conturul unitsquare scaled 1u (luând u=2.5cm), l-am translatat spre stânga și spre dreapta, apoi l-am dublat și l-am „așezat” deasupra (programul este banal și încă nu-i de redat aici).

Cazul particular „veritabil” (mai apropiat figurii inițiale) este următorul:

Prin vârful $A$ al pătratului $ABCD$ se duce dreapta $Ax$, paralelă diagonalei $BD$ (spre deosebire de cazul general, când $Ax$ este o dreaptă oarecare); se proiectează pe $Ax$ vârfurile $B$ și $D$ și se construiesc (spre dreapta și respectiv, spre stânga) pătratele $BEFG$ și $DHIJ$.
Pe $CG$ și $CJ$ se ridică pătratele $CGKL$ și $CJMN$.
Cum este aria triunghiului $CLN$, față de aria pătratului $ABCD$?

Cele 4 pătrate bazate pe dreapta $Ax$ au laturile egale cu $BO$ (= $\frac{a\sqrt{2}}{2}$).
Din $\triangle COG$, dreptunghic în $O$, avem: $$\tan\alpha=\frac{CO}{GO}=\frac{1}{2}$$

Unghiul $\angle CBO$ (de $45^{\circ}$) este exterior $\triangle CBG$ – deci măsoară cât $\alpha+\beta$, de unde: $$\beta = 45^{\circ} - \alpha = 45^{\circ} - \arctan\frac{1}{2}$$

Uitându-ne în jurul punctului $C$, avem: $\theta = 360^\circ - 3*90^\circ - 2\beta = 90^\circ - 2\beta$, adică: $$\theta = 2\arctan\frac{1}{2}$$

Aria $\triangle NCL$ este $\frac{CN\times CL\times \sin\theta}{2}=\frac{CN^2\sin\theta}{2}$ (semiprodusul a două laturi cu sinusul unghiului lor); rămâne să calculăm cele două laturi, care de fapt sunt egale.

În $\triangle CBG$ avem $CB=a$, $BG = \frac{a\sqrt{2}}{2}$, și $\measuredangle CBG = 180^\circ - (\alpha+\beta)$; teorema cosinusului ne dă: $CG^2=a^2+\frac{a^2}{2}-2a\frac{a\sqrt{2}}{2}cos(180^\circ-(\alpha+\beta))$ și ținând cont că $\alpha+\beta=45^\circ$, rezultă: $$CG^2 = \frac{5a^2}{2}\quad (= CN^2)$$

Deci aria $\triangle NCL$ este $\frac{5a^2}{4}\sin\theta=\frac{5a^2}{4}\sin(2\arctan\frac{1}{2})$.

Dar (v. un manual, sau un tabel de formule) $$\arctan x = \arcsin\frac{x}{\sqrt{1+x^2}}$$

deci $\arctan\frac{1}{2}=\arcsin\frac{\sqrt{5}}{5}$.

Rezultă că aria $\triangle NCL$ este $\frac{5a^2}{4}\times 2\sin(\arcsin\frac{\sqrt{5}}{5})\times \cos(\arcsin\frac{\sqrt{5}}{5}) = \frac{5a^2}{4}\times\frac{4}{5} = a^2$, adică: aria $\triangle NCL$ este egală cu aria pătratului $ABCD$.

Amintim că $\sin 2x=2 \sin x \cos x$; iar $\sin(\arcsin x)=x$ și $\cos(\arcsin x) = \sqrt{1-x^2}$;
teorema cosinusului: $a^2=b^2+c^2-2bc\cos A$

Programul MetaPost prin care am construit ultima figură este iarăși banal și nu-l redăm aici (v. totuși, de exemplu Cum construieşti un patrulater (sau, o asemănare)?).

În partea a II-a ne vom ocupa de cazul general, când dreapta $Ax$ este înclinată cu un unghi oarecare, față de diagonala $BD$.