În graful K plotat mai jos, avem această distribuție după grade a vârfurilor:

> table(degree(K))
     2  3  4  6  8   # grad
     4  8 20 16 16   # frecvență

și această distribuție a culorilor aplicate vârfurilor:

> table(V(K)$color)
     1  2  3  4   # culoare
    24 14 18  8   # frecvență

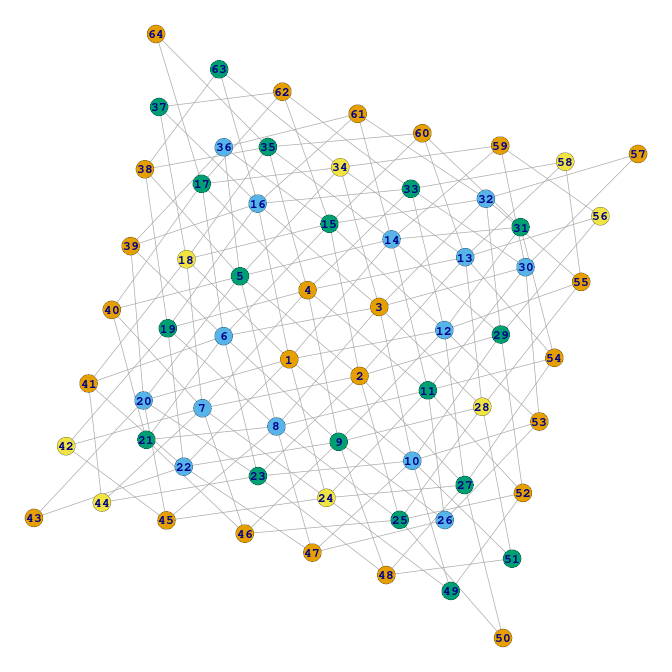
Pentru colorarea vârfurilor am folosit întâmplător (adică, fără să judecăm dacă este cazul) funcția greedy_color_by_centrality() din [1]; însă constatarea obținută – că ar fi necesare 4 culori – este greșită (am observat deja în [1], că dacă sunt multe vârfuri de o aceeași „centralitate”, atunci pot rezulta colorări care nu sunt optime).

Se vede ușor pe desenul redat, că graful K are 64 de vârfuri; „colțurile” 64 57 50 43 au fiecare gradul 2, iar celelalte vârfuri de pe „laturi” au gradul fie 3, fie 4; vârfurile din centru 1 2 3 4 (precum și cele alăturate centrului) au fiecare, gradul 8…
Deci K este „graful calului” pe tabla de șah 8×8. Dar tabla de șah are câmpuri de două culori, iar calul sare de pe „alb” pe „negru” (sau invers) – deci K poate fi colorat cu numai două culori (altfel spus, K este un graf bipartit). E clar că pentru grafurile bipartite nu (prea) este cazul să aplicăm vreun algoritm de colorare a vârfurilor…

În treacăt fie spus, K nu poate fi redat ca graf planar, fiindcă are prea multe (168) muchii (un graf conex, bipartit și planar are cel mult 2n-4 muchii, n fiind numărul de vârfuri).

De observat că am etichetat vârfurile în ordinea descrescătoare a „centralităților” (care pentru K este cam aceeași, cu ordinea descrescătoare a gradelor): am plecat din centru (și nu dintr-un colț, cum se obișnuiește pentru grafuri asociate cu tabla de șah) și am parcurs câmpurile în spirală (d4, e4, e5, d5, c5, c4, c3, d3, e3, f3, f4, f5, ...) – deschizând deci un nou subiect: generarea de „matrici-spirală”…