Cardioida $\mathcal{R}$ cu nodul în $\mathsf{O}(0,0)$ şi vârful în $\mathsf{A}(2a,0)$ are ecuaţiile parametrice (v. [1]) $$x=2at(2t-1),\; y=\pm 4at\,\sqrt{t(1-t)};\quad t\in[0,1]$$ şi ea este (faţă de reperul implicit, definit de originea $\mathsf{O}$ şi axa $\mathsf{OA}$) pătratul cercului cu centrul $(\sqrt{a/2\,},0)$ şi raza $\sqrt{a/2\,}$ (v. [2]):

$\mathcal{R}^2$ (adică mulţimea punctelor de afix $z^2$ când punctul de afix $z$ parcurge $\mathcal{R}$) aminteşte –doar– de o trisectoare Pascal ($\mathcal{T}$); plotând $z^2=(x^2-y^2)+i\cdot 2xy$ pentru $t\in[0,1]$, apoi separat pentru $t\in[0,\frac{1}{2}]$ şi respectiv $t\in[\frac{1}{2},1]$, obţinem:

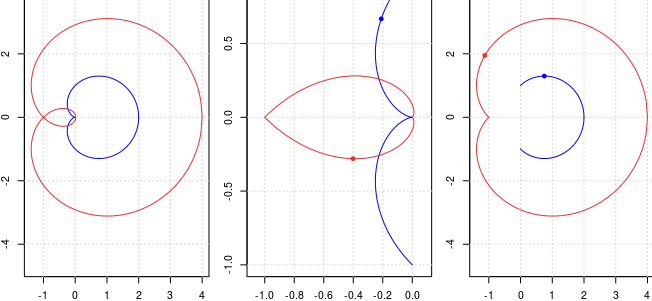
Figura din mijloc decupează (la scară mai mare) bucla interioară a lui $\mathcal{R}^2$ şi apare clar (cel puţin în jurul originii) că aceasta diferă, de cea specifică pentru $\mathcal{T}$; chiar şi fără vreun calcul, deducem că pătratul unei cardioide (cel puţin, în raport cu nodul şi axa acesteia) nu este o trisectoare Pascal.

Ceea ce vedem (mai adăugând şi cercul iniţial) ne sugerează în continuare două chestiuni:
$\quad$ 1. care curbă are ca pătrat $\mathcal{T}$?
$\quad$ 2. cum caracterizăm puterile naturale ale cercului tangent în $\mathsf{O}$ axei verticale ? (de mai sus, pătratul acestuia este cardioida $\mathcal{R}$, iar puterea a 4-a este $\mathcal{R}^2$).

Răspundem la prima chestiune (după [3], unde evidenţiasem o "pseudo-cardioidă", ca parte a radicalului complex al lui $\mathcal{T}$), dar numai pentru a o pregăti cumva pe a doua (unde vom vedea că obţinem curbe "similare", ţinând recurent de o aceeaşi familie).

Trisectoarea Pascal este pătratul unei pseudo-cardioide

Luându-ne după [3], să considerăm curba $\mathcal{S}$ cu ecuaţia polară $$\rho=\sqrt{a\cos\frac{2\theta}{3}\,},\;\theta\in[-3\pi/4,\,3\pi/4]\;\;(a\gt 0)$$

Pătratul punctului $(\rho,\theta)$ este punctul $(\rho^2,2\theta)$ şi notând $2\theta=\varphi$, rezultă că $\mathcal{S}^2$ are ecuaţia polară $r=a\cos\frac{\varphi}{3}$; aceasta reprezintă o trisectoare Pascal, deci avem $\mathcal{S}^2=\mathcal{T}$:

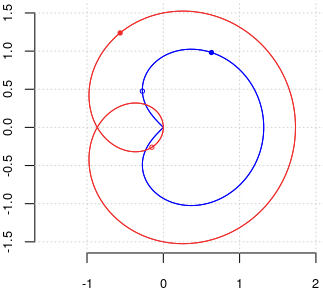
(am luat aici $a=\sqrt{3}$; cu albastru avem $\mathcal{S}$, iar cu roşu $\mathcal{T}=\mathcal{S}^2$)

Ca formă, $\mathcal{S}$ aminteşte de cardioidă (şi i-am zis "pseudo-cardioidă"), dar nu este o cardioidă (argumentând ca şi în [3]: coarda verticală şi cea orizontală, duse prin $\mathsf{O}$, au lungimi diferite).
Cu ridicări la pătrat - prin care însă, adaugăm şi opusa lui $\mathcal{S}$ faţă de origine - putem găsi ecuaţia carteziană corespunzătoare: $$f(x,y)=4(x^2+y^2)^4-3a^2(x^2+y^2)^2+a^3(y^2-x^2)=0$$

(putem exprima $\cos^2\frac{\theta}{3}$ din $x^2+y^2=\rho^2=a\cos\frac{2\theta}{3}=a(2\cos^2\frac{\theta}{3}-1)$ şi apoi înlocuim în $x^2=\rho^2\cos^2\theta=\rho^2\cos^2\frac{\theta}{3}(4\cos^2\frac{\theta}{3}-3)^2$, ajungând la (3))

Ecuaţia implicită $f(x,y)=0$ ne-ar folosi pentru a vedea cum rezultă $\mathcal{S}$ (dar împreună cu simetrica ei faţă de $\mathsf{O}$) ca secţiune plană prin suprafeţele $f(x,y)=z$; ca şi în [3] (unde aveam $a=2$), putem constata că rezultă curbe care seamănă cu un "Dürer folium".

Procedând ca în [2] (plecând de la $x^2+y^2=at$), putem obţine pentru $\mathcal{S}$, ecuaţiile parametrice: $$x=\sqrt{\frac{a}{2}\,}(2t-1)\sqrt{t(1+t)\,},\;y=\pm\sqrt{\frac{a}{2}\,}(2t+1)\sqrt{t(1-t)\,};\;t\in[0,1]$$

Cu acestea putem determina diverse caracteristici numerice al lui $\mathcal{S}$ (v. [3]); dar în acest scop putem foarte bine să folosim direct forma polară - încât trebuie să recunoaştem că ecuaţiile parametrice "cu radical" redate mai sus nu prea merită atenţie (afară de faptul că "izolează" ramura $\mathcal{S}$ din curba de gradul 8 reprezentată de $f(x,y)=0$).

Proprietăţi geometrice ale puterilor cercului

Considerăm cercul $\mathcal{C}$ cu centrul $\mathsf{A}(1,0)$ şi rază $\mathsf{OA}=1$.

Notăm cu $\rho$ şi $\theta$ coordonatele polare (faţă de originea $\mathsf{O}$ şi axa $\mathsf{OA}$) ale unui punct oarecare $\mathsf{P}$ al lui $\mathcal{C}$; ducând $\mathsf{AM}\perp\mathsf{OP}$, avem $\mathsf{OM}=\mathsf{OA}\cos\theta=\cos\theta$ şi (fiindcă $\mathsf{M}$ este mijlocul coardei) urmează că $\rho=\mathsf{OP}=2\mathsf{OM}=2\cos\theta$.

Deci ecuaţia polară a lui $\mathcal{C}$ (faţă de punctul $\mathsf{O}$ al său şi axa dată de diametrul dus prin $\mathsf{O}$) este: $\rho=2\cos\theta$ (cu $\theta\in[0,\pi]$); iar coordonatele carteziene sunt $x=\rho\cos\theta=2\cos^2\theta$ şi $y=\rho\sin\theta=2\cos\theta\sin\theta$.
Obs. De obicei, pentru $\theta$ se indică mecanic intervalul $[0,2\pi]$; dar $\cos^2\theta$ şi $\sin 2\theta$ prin care se exprimă $x$ şi $y$, au perioada $\pi$ (cu $\theta\in[0,2\pi]$, cercul va fi parcurs sau trasat de două ori).

Fie $n$ un număr natural nenul; puterea $n$ a punctului $\mathsf{P}(\rho,\theta)$ este punctul $\mathsf{P}^n(\rho^n,n\theta)$, iar curba descrisă de $\mathsf{P}^n$ este puterea $n$ a curbei descrise de $\mathsf{P}$. În cazul nostru, când $\mathsf{P}$ parcurge cercul $\mathcal{C}$, coordonatele lui $\mathsf{P}^n$ (sau ecuaţiile parametrice ale lui $\mathcal{C}^n$) sunt $x_n=(2^n\cos^n\theta)\cos n\theta$ şi $y_n=(2^n\cos^n\theta)\sin n\theta\,$ sau, mai concis (ca numere complexe): $$z_n(\theta)=2^n(\cos^n\theta)\,\mathsf{e}^{n\theta i},\;\theta\in[0,\pi]\quad\quad\quad\small(1)$$

Este clar că $\mathcal{C}^n$ este conţinut în discul de rază $2^n$ centrat în origine. Am ales $[0,\pi]$ pentru $\theta$ fiindcă avem $z_n(\theta+\pi)=z_n(\theta)$, adică punctele lui $\mathcal{C}^n$ se repetă (dacă $\theta$ n-ar fi restricţionat) cu periodicitatea $\pi$; probabil ar fi mai greu să demonstrăm că $\pi$ este chiar "perioada principală", dar graficele lui $x_n(\theta)$ şi $y_n(\theta)$ (pentru câteva valori $n$) ne încredinţează că aşa este.

Fiindcă $z_n(\pi-\theta)=z_n(-\theta)=\overline{z_n(\theta)}$ şi $z_n(\frac{\pi}{2})=0$, deducem că graficele descrise când $\theta$ parcurge (crescător) intervalul $[0,\frac{\pi}{2}]$ şi respectiv, când $\theta$ parcurge (descrecător) $[\frac{\pi}{2},\pi]$ sunt simetrice faţă de axa reală. Prin urmare, va fi suficient în general, să presupunem $\theta\in[0,\frac{\pi}{2}]$.
Obs. Dacă $z_n(\theta)$ are partea imaginară nulă, atunci $\overline{z_n(\theta)}=z_n(\theta)$; deci punctele lui $\mathcal{C}^n$ aflate pe axa $y=0$ sunt "puncte duble" (fiecare se obţine pentru o anumită valoare $\theta$, dar apoi şi pentru $\pi-\theta$).

Avem imediat relaţia de recurenţă: $$z_{n+1}(\theta)=z_n(\theta)\cdot(2\cos \theta)\,\mathsf{e}^{i\theta},\;\theta\in[0,\pi]\;\;(n\in\mathbb{N^*})\quad\quad\quad\small(2)$$

Aceasta ne spune că punctul $\mathsf{P}^{n+1}(\theta)$ se obţine din punctul $\mathsf{P}^n(\theta)$ prin scalarea razei $\mathsf{OP}^n$ cu factorul $2|\cos\theta|$ şi rotirea în jurul lui $\mathsf{O}$ a punctului rezultat astfel, cu unghiul $\theta$ (sau cu $\pi+\theta$, dacă $\cos\theta\lt 0$, adică dacă $\theta\in(\pi/2, \pi)$):

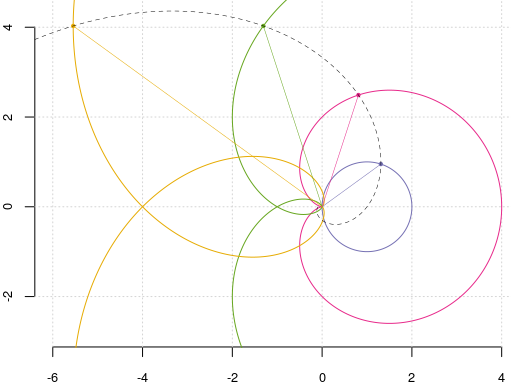
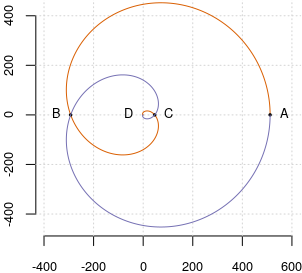
Am reprezentat aici (prin culori diferite şi restrângând în jurul originii) curbele $\mathcal{C}^n$ pentru $n=1..4$ (cercul iniţial, cardioida care este pătratul acestuia, puterea 3 a cercului, ş.a.m.d.), pe care am marcat punctele $\mathsf{P}^n(\frac{\pi}{5})$ şi razele $\mathsf{OP}^n$; linia punctată face parte dintr-o anumită spirală logaritmică.

Fixăm o valoare $\theta$ (presupunem pentru simplitate, $\theta\in(0,\pi/2)$); vom mai nota $\mathsf{P}^n$ în loc de $\mathsf{P}^n(\theta)$ . Avem un lot de observaţii sau proprietăţi, pe care le justificăm "una din alta", mai jos:

$\mathsf{OP}^n\mathsf{P}^{n+1}$ sunt triunghiuri isoscele asemenea între ele ($n\in\mathbb{N}^*$).
Mediatoarea segmentului $\mathsf{OP}^{n+1}$ este tangentă în $\mathsf{P}^n$ la $\mathcal{C}^n$.
$\mathcal{C}^{n+1}$ este orthotomica (asemenea cu podara) faţă de $\mathsf{O}$ a lui $\mathcal{C}^n$.
Tangenta în $\mathsf{P}^n(\theta)$ la $\mathcal{C}^n$ are panta egală cu $-\mathrm{ctg}\,(n+1)\theta$.
Punctele $\mathsf{P}^n(\theta),\,\small n\in\mathbb{N^*}$ (cu acelaşi $\theta$) aparţin unei aceleiaşi spirale logaritmice.
$\mathcal{C}^{3n}$ are un punct de întoarcere (prin care trece de două ori) în $((-1)^n,0)$.

Într-adevăr, fie $\mathsf{M}$ piciorul perpendicularei din $\mathsf{P}^n$ pe $\mathsf{OP}^{n+1}$; avem $\mathsf{OM}=\mathsf{OP}^n\cos\theta$ (fiindcă $\mathsf{P}^{n+1}$ s-a obţinut din $\mathsf{P}^n$ în urma unei scalări şi apoi, printr-o rotaţie în jurul lui $\mathsf{O}$ cu unghiul $\theta$) şi cum $\mathsf{OP}^{n+1}=\mathsf{OP}^n\cdot 2\cos\theta$ rezultă că $\mathsf{OP}^{n+1}=2\,\mathsf{OM}$, adică $\mathsf{M}$ este mijlocul segmentului $\mathsf{OP}^{n+1}$. Având $\mathsf{P}^n\mathsf{M}$ şi ca mediană şi ca înălţime, urmează că $\mathsf{OP}^n\mathsf{P}^{n+1}$ este triunghi isoscel; având unghiurile de la bază egale cu $\theta$ (care fusese fixat iniţial), toate aceste triunghiuri (pentru $n\in\mathbb{N}^*$) sunt asemenea între ele.

Dacă $\mathsf{MP}^n$ ar tăia $\mathcal{C}^k$ într-un al doilea punct $\mathsf{R}(\theta ')\ne\mathsf{P}^n$, atunci am avea $\mathsf{OM}=\mathsf{OR}\cos\theta '$ deci $\mathsf{OP}^{n+1}=\mathsf{OR}\cdot 2\cos\theta '$; dar scalând $\mathsf{OR}$ (unde $\mathsf{R}\in\mathcal{C}^n$) cu $2\cos\theta '$ şi rotind rezultatul cu $\theta'$ ajungem la $z_{n+1}(\theta')$ şi ar rezulta că $z_{n+1}(\theta)=z_{n+1}(\theta')$ ceea ce înseamnă (exceptând poate, câteva cazuri particulare) că $\theta=\theta'$ (în contradicţie cu presupunerea că $\mathsf{R}$ diferă de $\mathsf{P}^n$). Rezultă că $\mathsf{MP}^n$ (mediatoarea segmentului $\mathsf{OP}^{n+1}$) este într-adevăr, tangentă la $\mathcal{C}^n$.
Altfel spus, $\mathsf{P}^{n+1}$ este simetricul lui $\mathsf{O}$ faţă de tangenta în $\mathsf{P}^n$ la $\mathcal{C}^n$; deci punctele lui $\mathcal{C}^{n+1}$ sunt simetricele lui $\mathsf{O}$ faţă de tangentele lui $\mathcal{C}^n$, adică $\mathcal{C}^{n+1}$ este orthotomica lui $\mathcal{C}^n$ (iar locul punctelor $\mathsf{M}$ - adică podara lui $\mathcal{C}^n$ - este omotetica de raport 1/2 şi pol $\mathsf{O}$ a lui $\mathcal{C}^{n+1}$).

Fiindcă tangenta în $\mathsf{P}^n(\theta)$ la $\mathcal{C}^n$ este mediatoarea segmentului $\mathsf{OP}^{n+1}$, iar unghiul polar al lui $\mathsf{P}^{n+1}(\theta)$ este egal cu $(n+1)\theta$, rezultă că unghiul cu axa reală al tangentei respective este $\frac{\pi}{2}-(\pi-(n+1)\theta)$; deci panta tangentei este $\mathrm{tg}((n+1)\theta-\frac{\pi}{2})=-\mathrm{ctg}(n+1)\theta$.

Fiindcă şirul razelor polare $\mathsf{OP}^n(\theta),\,n\in\mathbb{N^*}$ este o progresie geometrică (de raţie $2\cos\theta$), iar unghiurile polare corespunzătoare constituie o progresie aritmetică (de raţie $\theta$) - urmează că punctele $\mathsf{P}^n$ sunt situate pe o anumită spirală logaritmică. Ecuaţia acesteia poate fi obţinută (în cel mai simplu mod) din (1), punând $n\theta=t$: $$z_{\theta}(t)=(2\cos\theta)^{t/\theta}\mathsf{e}^{it},\,t\in\mathbb{R^*};\;\theta\in(0,\pi/2)\quad\quad\quad\small(3)$$

Să observăm că avem un caz aparte: pentru $\theta=\pi/3$ spirala "degenerează" într-un cerc (avem $\cos\frac{\pi}{3}=0.5$, deci $z_{\pi/3}(t)=\mathsf{e}^{it}$, reprezentând cercul unitate); figura următoare arată pentru acest caz (restrângând în jurul originii), curbele $\mathcal{C}^n$ (până la $n=6$) şi intersecţiile $\mathsf{P}^n(\pi/3)$:

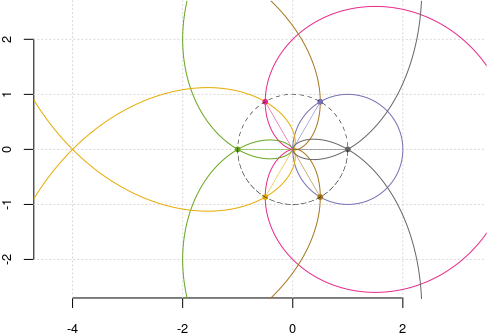
De fapt, din (1) avem $z_n(\frac{\pi}{3})=\mathsf{e}^{ni\frac{\pi}{3}},\,\forall n\in\mathbb{N}^*$ deci toate curbele $\mathcal{C}^n$ trec prin câte două vârfuri (simetrice faţă de $\mathsf{O}x$, eventual confundate) ale hexagonului regulat constituit de rădăcinile de ordinul 6 ale unităţii. Când $n$ este multiplu de 3, cele două vârfuri menţionate se confundă fie în $(-1,0)$, fie în $(1,0)$; adică $\mathcal{C}^{3k}$ trece de două ori fie prin $(-1,0)$ (când $k$ este impar), fie prin $(1,0)$ (când $k$ este par).

Pentru $\small n=3$, (1) devine $z_3(\theta)=8\cos^3\theta\,\mathsf{e}^{3\theta i},\,\theta\in[0,\pi]$ şi putem identifica $\mathcal{C}^3$ (cubul cercului de rază 1 cu centrul (1, 0)) în familia de curbe sextica lui Cayley. Putem neglija $\mathcal{C}$ (cercul iniţial), $\mathcal{C}^2$ (cardioida) şi $\mathcal{C}^3$ (sextica lui Cayley) - acestea trei fiind desigur, binecunoscute (mai puţin probabil, această explicitare: sextica lui Cayley este cubul unui anumit cerc); ceea ce pare a fi încă necatalogat începe de la $n=4$.

Dileme grafice, pe un caz particular

În R este foarte uşor să facem grafice (în orice caz, mai simplu sau mai scurt, decât în alte limbaje). Definim întâi o funcţie care să returneze punctele (sau doar un punct individual) de pe $\mathcal{C}^n$:

Cn <- function(k, th=NULL, from=0, to=pi) {
    if(is.null(th))  th <- seq(from, to, by=0.0001)
    2^k*(cos(th))^k*exp(1i*k*th)
}

Cu z <- Cn(9) am obţine în variabila z punctele lui $\mathcal{C}^9$, calculate după formula (1), $\theta$ parcurgând cu pasul 0.0001 intervalul de la 0 la π. Cu z <- Cn(9, to = pi/2) vom obţine numai punctele lui $\mathcal{C}^9$ corespunzătoare intervalului $[0,\pi/2]$ (parcurs cu pasul 0.0001).
Cu E <- Cn(9, 4*pi/9) vom obţine în variabila E punctul $\mathsf{P}^9(\frac{4\pi}{9})$, aflat pe $\mathcal{C}^9$.

Fixăm $n$ (sau lăsăm ca $n$ să fie ales prin sample() (aleatoriu) dintr-un anumit interval, la fiecare executare a programului), obţinem (apelând funcţia Cn()) punctele z ale curbei $\mathcal{C}^n$, apelăm plot() cu type="n" (prin care doar se vor determina limitele absciselor şi ordonatelor) şi cu asp=1 (vrând unităţi egale pe axe) şi apoi folosim points(), obţinând graficul:

n <- 9  # n <- sample(1:25, 1)
z <- Cn(n, to=pi/2)
plot(z, type="n", asp=1); grid()  # limitele ferestrei grafice
points(z, type="l")  # plotează punctele 'z', unindu-le consecutiv

Salvăm cele 7 linii de program redate mai sus într-un fişier text "cerc.R" (pe care îl vom putea ulterior modifica sau completa), lansăm o sesiune interactivă de R şi la promptul specific tastăm comanda source("cerc.R"), punând în execuţie programul respectiv.

Dar (orice limbaj de programare şi orice trucuri am folosi), se poate ca graficul obţinut (depinzând de rezoluţia de afişare impusă şi de erorile de rotunjire) să nu reflecte mulţumitor, realitatea matematică:

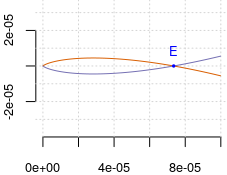
În stânga avem graficul lui $\mathcal{C}^9$; cu $\theta$ de la $0$ până la $\frac{\pi}{2}$ s-a parcurs arcul A-B-C-D, marcat cu maro; apoi, cu $\theta$ de la $\frac{\pi}{2}$ până la $\pi$ s-a parcurs arcul marcat cu o nuanţă albastră D-C-B-A. Dacă ne luăm după ce vedem pe acest grafic, $\mathcal{C}^9$ ar avea pe axa $y=0$ doar cele patru puncte menţionate (între care, două "puncte de întoarcere" - B şi C); în realitate, punctele din vecinătatea originii au valori aşa de mici încât nu au putut fi reprezentate (la scara indicată pe grila adăugată graficului), încât "punctul" notat cu D maschează de fapt mai multe puncte ale curbei.

Graficul din dreapta corespunde unui interval restrâns în jurul lui $\frac{\pi}{2}$ (cu $\pm 0.3$), fiind selectate şi plotate numai punctele cu distanţa mai mică decât $10^{-4}$ faţă de origine; iese la iveală acum că lângă D există cel puţin încă un punct cu $y=0$, cel marcat cu E (şi este un al treilea "punct de întoarcere", de abscisă pozitivă foarte mică, ≈ 7*10-5).
Iar modul în care intră arcul maro în E, continuând spre origine, contrazice cumva sensul în care este parcurs arcul C-D - ceea ce dă de bănuit că în realitate curba buclează (sau "spiralează") de mai multe ori în jurul originii (apropiidu-se de O(0,0)), până ce în sfârşit, se parcurge arcul maro E-O (în acelaşi sens ca C-D) şi se continuă cu partea albastră O-E, mergând probabil spre C… Originea este cu siguranţă, un punct cu totul special pentru $\mathcal{C}^n$.

Punctele duble (şi alte puncte speciale) de pe $\mathcal{C}^n$

În general, punctele "speciale" sunt cele de discontinuitate (dacă există), cele prin care graficul trece de mai multe ori (punctele "duble", sau mai general "multiple"), punctele de inflexiune (dacă există), cele în care graficul are tangente sau semitangente cu anumite pante particulare.

Să găsim întâi, punctele în care $\mathcal{C}^n$ taie axa $y=0$. Din (1) avem $y_n=2^n\cos^n\theta\sin n\theta$ şi putem presupune (exceptând probabil, comportarea "în jurul" lui $\frac{\pi}{2}$) că $\theta\in[0,\frac{\pi}{2}]$; factorul $\sin n\theta$ se anulează pentru $\theta=\frac{k\pi}{n},\,k=0..[\frac{n}{2}]$, iar pentru $k=\frac{n}{2}$ (dacă $n$ este par) obţinem şi rădăcina factorului $\cos^n\theta$ (acesta fiind "la puterea $n$", urmează bănuiala că $\theta=\frac{\pi}{2}$ induce o multiplicitate de ordinul $n$ pentru punctul respectiv). Prin urmare, $\mathcal{C}^n$ taie axa $y=0$ în $[\frac{n}{2}]+1$ puncte distincte (plus, dacă $n$ este impar, punctul pentru $\theta=\frac{\pi}{2}$) şi anume (ţinând cont în (1) că $\mathsf{e}^{k\pi i}=(-1)^k$): $$z_n\left(\frac{k\pi}{n}\right)=\left((-1)^k\,2^n\cos^n\frac{k\pi}{n},\,0\right),\;k=0\,..\left[\frac{n}{2}\right]\quad\quad\quad\small(4)$$

De exemplu pentru $\mathcal{C}^9$ aceste puncte sunt tocmai A..E (respectiv, pentru $k=0..4$) marcate pe figura de mai sus, al şaselea (pentru $\theta=\frac{\pi}{2}$) fiind originea O; putem intui acum traseul curbei maro: din D (care este punctul $z_9(3\pi/9)=(-1,0)$) se ajunge pe dedesubtul axei $y=0$ în E (distanţat în dreapta lui O cu mai puţin de 8 sutimi de miime), de unde buclează spre O (care este un punct multiplu) şi apoi încheie înapoi spre D cum am descris deja mai sus.

Punctele (4) (exceptând $k=0$ şi dacă $n$ este par, $k=\frac{n}{2}$) sunt puncte duble (sau puncte de întoarcere) pentru $\mathcal{C}^n$.
Unghiurile cu axa $y=0$ ale tangentelor în punctele de întoarcere ale $\mathcal{C}^n$ sunt unghiuri suplementare.

Într-adevăr, avem $z_n(\pi-\theta)=\overline{z_n(\theta)}$ (cum observasem deja la (1)); dar punctele (4) au partea imaginară nulă, deci pentru ele (adică pentru $\theta=\frac{k\pi}{n}$) avem $\overline{z_n(\theta)}=z_n(\theta)$. Cu alte cuvinte, fiecare dintre aceste puncte prin care intră "arcul maro" (corespunzător parcurgerii curbei cu $\theta$ de la $0$ la $\frac{\pi}{2}$) este un punct de întoarcere al curbei: "arcul albastru" (corespunzător parcurgerii curbei cu $\theta$ de la $\frac{\pi}{2}$ la $\pi$) va trece deasemenea, prin acel punct.
Am văzut anterior că tangenta într-un punct dat de (1) al lui $\mathcal{C}^n$ are panta $-\mathrm{ctg}\,(n+1)\theta$; în punctele de întoarcere pantele sunt $-\mathrm{ctg}\,(n+1)\frac{k\pi}{n}$ şi $-\mathrm{ctg}\,(n+1)(\pi-\frac{k\pi}{n})$ deci (fiindcă $\mathrm{ctg}()$ are perioada $\pi$) tangentele într-un punct de întoarcere (la "arcul maro", respectiv la "arcul albastru") au pantele "egale şi de semn contrar", deci unghiurile menţionate sunt suplementare (desigur, ne-am putea lipsi de acest calcul cu pante: în fond, "arcul maro" şi "arcul albastru" sunt simetrice faţă de $y=0$, deci tangentele în punctele de întoarcere sunt şi ele, simetrice faţă de $y=0$).

Dar să profităm încă de faptul că ştim panta pentru orice tangentă la $\mathcal{C}^n$. În câte puncte şi în care anume, avem tangente orizontale (de pantă zero)? Avem $\mathrm{ctg}\,(n+1)\theta=0$ numai când $(n+1)\theta=\frac{\pi}{2}+k\pi$ şi fiindcă $\theta\le\pi$ rezultă $k\le n+\frac{1}{2}$. Rezultă această proprietate:

pe $\mathcal{C}^n$ există exact $n+1$ puncte în care tangenta este orizontală şi anume, cele corespunzătoare prin (1) pentru $\theta=\frac{\pi}{2(n+1)}+\frac{k\pi}{n+1},\,k=0..n$.

Pentru $k=\frac{n}{2}$ am obţine $\theta=\frac{\pi}{2}$, care corespunde originii $\mathsf{O}(0,0)$; ar reieşi că pentru $n$ par, $\mathcal{C}^n$ este tangentă în origine axei $y=0$ - dar aceasta este o afirmaţie încă discutabilă (originea fiind punct multiplu de ordinul $n$).

La fel constatăm (plecând de la condiţia $(n+1)\theta=k\pi$) că există exact $n+2$ puncte în care $\mathcal{C}^n$ are tangentă verticală - cele corespunzătoare valorilor $\theta=\frac{k\pi}{n+1},\,k=0..n+1$.

Să observăm că aici am fost într-un caz fericit, putând calcula direct panta tangentei la curbă în oricare punct; dar de obicei, evidenţierea punctelor "speciale" se bazează pe derivatele funcţiei care defineşte ecuaţia curbei (de exemplu, punctele în care graficul are tangente orizontale sunt date de rădăcinile derivatei întâia). Pentru a calcula totuşi derivatele funcţiei date de (1) (precizăm că în principiu, regulile de derivare pentru funcţii de variabilă complexă sunt aceleaşi pe care le ştim de la funcţii reale) putem profita ca şi pentru (2), de recurenţă.

Avem $z_n\,'(\theta)=2^n\left(-n\cos^{n-1}\theta\,\sin\theta\,\mathsf{e}^{n\theta i}+ni\,\mathsf{e}^{n\theta i}\cos^n\theta\right)$; dar $\cos\theta-i\sin\theta=\mathsf{e}^{-i\theta}$, încât obţinem $z_n\,'=i\,n\,2^n\cos^{n-1}\theta\;\mathsf{e}^{(n-1)\theta i}$ şi putem exprima în funcţie de $z_{n-1}$: $$z_n\,'(\theta)=2\,i\,n\,z_{n-1}(\theta)$$

Iterând de $k=1..n-1$ ori, găsim uşor expresia derivatei de ordinul $k$: $$z_n^{\,(k)}(\theta)=i^k2^kn(n-1)\cdots(n-k+1)\,z_{n-k}(\theta)\quad\quad\quad\small(5)$$

Toate aceste derivate (dar nu şi $z_n^{\,(n)}(\theta)=i^n2^nn!\,\mathsf{e}^{2\theta i}$) se anulează în $\theta=\frac{\pi}{2}$; rezultă că punctul $\mathsf{O}(0,0)$ (corespunzător pentru $\theta=\frac{\pi}{2}$) este "punct multiplu de ordinul n" pentru $\mathcal{C}^n$ (am vrea noi să lămurim mai precis dar mai simplu, ce înseamnă aceasta pentru grafic…).