Speculaţii asupra coardei frânte
Considerăm pe două direcţii distincte segmentele $BC$ şi $BA$, cu $BC\gt BA$; altfel spus, $B(CA)$ este o "coardă frântă" a unui anumit cerc.
Să rotim punctul $A$ în jurul lui $B$, până în punctul $D$ situat pe dreapta $BC$; astfel, $B$ aparţine mediatoarei segmentului $AD$ şi fie $M$ intersecţia acesteia cu mediatoarea lui $CD$; notăm cu $E$ mijlocul laturii $CD$:
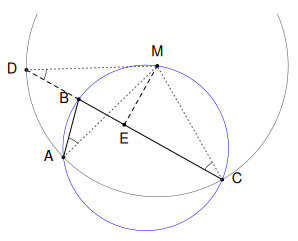
Atunci avem evident $CE=DE=BD+BE=BA+BE$; deci $E$ este "mijlocul" coardei frânte $B(CA)$ (dar să recunoaştem că încă nu avem vreun motiv pentru a folosi denumirea de "coardă frântă"!).
Pe de altă parte, cele trei unghiuri marcate pe figură sunt egale (fiindcă $M$ este egal depărtat de $A$ şi $C$, iar $B$ este egal depărtat de $A$ şi $D$); deci $MBAC$ este patrulater inscriptibil (iar $M$ este mijlocul arcului de cerc $(ABC)$). Regăsim astfel, formularea iniţială pentru "teorema coardei frânte" (atribuite lui Arhimede): dacă $M$ este mijlocul arcului $(ABC)$ iar $E$ este proiecţia lui $M$ pe $BC$ atunci $AB+BE=CE$ (iar în acest context devine firească şi denumirea "coardă frântă").
Prima construcţie este cea mai simplă posibilă: se prelungeşte $BC$ cu $BD=BA$; mijlocul lui $CD$ este tocmai "mijlocul" coardei frânte $B(CA)$.
În schimb, construcţia originală, care angajează mijlocul arcului $(ABC)$ este una importantă: pe baza ei s-au dedus formulele de bază ale trigonometriei, încă în vremurile în care numerele erau văzute ca lungimi sau rapoarte de lungimi (sau arii, volume), iar unghiurile erau măsurate prin lungimea corzii subântinse într-un cerc.
Astfel, dacă notăm cu $\alpha$ şi $\beta$ măsurile unghiurilor făcute de $MB$ şi $MC$ cu $BC$ şi considerăm raza cercului $(MBAC)$ ca fiind egală cu $1$, atunci avem $MC=2\sin\alpha$, $MB=2\sin\beta$ şi $AB=2\sin(\alpha-\beta)$, iar $BE=MB\cos\alpha$ şi $CE=MC\cos\beta$; din $AB+BE=CE$ rezultă astfel formula $\sin(\alpha-\beta)+\sin\beta\cos\alpha=\sin\alpha\cos\beta$. În termeni de "chord", această formulă era cunoscută lui Hipparchus, care (pentru a sprijini investigaţii de astronomie) a constituit primul "tabel trigonometric", conţinând lungimile coardelor corespunzătoare unghiurilor într-un anumit cerc.
Pentru o figură precum cea redată mai sus, avem un nou prilej de a exersa în R. Mai întâi evocăm nişte "funcţii utilitare" de care ne servim adesea pentru a crea comod segmente, puncte ale unui cerc şi arce de marcare pentru unghiuri:
draw_segment <- function(z2, z1, ...) { # uneşte punctele de afixe z1, z2 segments(Re(z1), Im(z1), Re(z2), Im(z2), ...) } draw_segments <- function(list_2z, ...) { for(z in list_2z) draw_segment(z[1], z[2], ...) } cerc <- function(s=NULL) { # puncte ale cercului |z|=1 if(is.null(s)) s <- seq(0, 2*pi, by=0.001) exp(1i*s) } draw_arc <- function(z1, z, z2) { # marchează unghiul z1_z_z2 a1 <- Arg(z2 - z) a2 <- Arg(z1 - z) h <- seq(min(a1, a2), max(a1, a2), by=0.001) points(z + 0.24*cerc(h), type="l", lwd=0.7, col="gray20") }
De exemplu, pentru a plota segmentele $BD$ şi $ME$ cu linie întreruptă vom putea folosi:
draw_segments( list(c(B, D), c(M, E)), lty="dashed" ); prin an <- pi/6; P <- cerc(an) obţinem punctul $P(\cos\frac{\pi}{6},\,\sin\frac{\pi}{6})$; prin points(cerc()) plotăm cercul unitar; iar prin draw_arc(M, C, E) vom marca grafic unghiul $\measuredangle{MCE}$.
Definim convenabil un panou grafic, în care să creem figura:
xlim <- c(-1.5, 1.5); ylim <- c(-1.5, 1.5) plot(0, type="n", asp=1, bty="n", xlab="", ylab="", xaxt="n", yaxt="n", xlim=xlim, ylim=ylim) # setează fereastra grafică, în mod convenabil
Definim punctele $B$, $C$ şi $A$ plecând de la nişte valori unghiulare sb, sc, sa (poate avem de încercat câteva valori, până obţinem o figură satisfăcătoare); constituim apoi şi punctele $D$, $M$ şi $E$. Marcăm punctele respective, trasăm segmentele, cercurile şi marcăm unghiurile:
sb <- 4*pi/5 sc <- -pi/8 sa <- 115*pi/111 B <- cerc(sb); C <- cerc(sc); A <- cerc(sa) M <- cerc((sa+sc)/2) # MD = MA = MC (M este mijlocul arcului CBA) D <- B + (A-B)*exp(1i*(pi-Arg((A-B)/(C-B)))) # roteşte A în jurul lui B, cu un # unghi egal cu suplementul unghiului CBA E <- (C+D)/2 # mijlocul segmentului CD points(c(B, C, A, M, D, E), pch=20, cex=0.6) draw_segments(list(c(B, C), c(B, A))) draw_segments(list(c(B, D), c(M, E)), lty="dashed") draw_segments(list(c(M, A), c(M, D), c(M, C)), lty="dotted", col="gray30") text(c(C, B, A, M, D, E), labels=c("C", "B", "A", "M", "D", "E"), pos=c(4, 2, 2, 3, 2, 1), cex=0.9) points(M + abs(C-M)*cerc(), # cercul circumscris triunghiului CAD type="l", lwd=0.5, col="gray30") draw_arc(M, C, E); draw_arc(M, A, B); draw_arc(M, D, B) points(cerc(), type="l", lwd=0.5, col="blue") # MCAB este inscriptibil
Pe figura constituită mai sus putem face uşor încă o speculaţie privind construcţia punctului $E$: bisectoarea unghiului $\measuredangle{ABC}$ este paralelă cu baza $AD$ a triunghiului isoscel $DBA$, la fel ca şi linia mijlocie prin $E$ a triunghiului $DAC$; deci putem construi $E$ ("mijlocul" coardei frânte) şi intersectând cu $BC$ paralela prin mijlocul lui $AC$ la bisectoarea unghiului $\measuredangle{ABC}$.
Dar subliniem: dintre cele trei metode de construcţie evidenţiate, aceea care este într-adevăr semnificativă (fiind implicată direct în constituirea treptată a aparatului trigonometric) şi care constituie cadrul firesc al denumirii de "coardă frântă" este construcţia originală a lui Arhimede (despre celelalte două am zice că sunt "speculaţii" pe figura formată din două segmente).
vezi Cărţile mele (de programare)