Instrumente tradiţionale şi instrumente moderne

Recent am avut de discutat în familie - implicând fireşte Internetul - o problemă de geometrie elementară. Fiind vorba de o problemă de clasa a VI-a (dar chiar nebanală) şi care viza unghiuri de 15° şi 30° - am optat fireşte pentru o construcţie prealabilă, cu rigla şi compasul; în general, pe o figură precisă poţi intui răspunsul şi îţi măreşti şansele de a "vedea" o rezolvare (în plus ar fi de mizat pe valenţele formative indubitabile ale practicării construcţiilor geometrice).

Acest context deschide două probleme generale: pe de o parte, constatăm că "instrumentele geometrice" au fost degradate: în şcoli, rigla serveşte in principal ca să tragi linie la caiet, iar compasul a fost înlocuit cu raportorul şi cu echerul; în proporţie de masă - şi deja de mai mulţi ani - elevii de clasa a IX-a nu ştiu să determine mijlocul unui segment şi "construiesc" unghiul drept folosind echerul (chit că, mai toţi elevii au nota 10 la obiectul întreţinut în şcoli sub numele "Desen").

Pe de altă parte, apare tacit o problemă de mediu binecunoscută: hârtie versus display. În cazul unei construcţii geometrice pot fi importante anumite etape intermediare, încât folosirea unui scanner este mai puţin potrivită pentru "digitizare", decât în cazul unei imagini statice sau al unei cărţi.

Dar poate că astăzi nu prea mai ai nevoie de hârtie, creion şi chiar nici de riglă şi compas (în acelaşi sens - nu mai mult - în care s-ar putea zice că "nu ai nevoie" de cărţi şi desigur, nici de pictori, sau de bucătari). Într-adevăr, există pachete software precum GeoGebra, care îţi permit să trasezi comod ("point-and-click") şi să analizezi figuri geometrice oricât de complexe (constituind în ansamblu, un excelent "material didactic").

Şi la fel ca în cazul hârtiei, compasului şi altor instrumente - iată că ne putem "debarasa" şi de scaner: putem folosi vreun program utilitar ca recordMyDesktop care înregistrează secvenţial imagini de pe desktopul propriu, constituind un fişier video-audio (un Screencast) care când va fi deschis de către destinatar, va reda pas cu pas construcţia şi demonstraţia.

Putem face multe lucruri utile folosind instrumentele moderne create prin diverse pachete software; dar să nu ne păcălim: ele pot simplifica, pot schematiza, sintetiza sau secvenţia şi pot îndosaria - dar nu pot înlocui nimic… Să nu confundăm cartea de bucate cu însuşi celebrul bucătar.

Enunţul problemei şi scopurile rezolvării de probleme

Reproduc (fără pretenţii de calitate) formularea din culegerea respectivă:

Este o formulare tipică pentru culegerile obişnuite de astăzi, care nu vizează triunghiul ci "triunghiul ABC"; nu lungimea este vizată, ci "lungimea de 5 cm", etc. (iar modul de folosire a limbii este deja neimportant). În orice caz - culegerea apare ca fiind o enumerare de enunţuri indexate, servind profesorului pentru a indica elevilor săi tema suplimentară pentru acasă.

O formulare naturală (cu siguranţă, mai frumoasă) ar fi aceasta:

La baza unui triunghi sunt unghiuri de 15 şi respectiv 30 de grade. Se cere unghiul dintre mediana şi înălţimea duse din vârful opus bazei.

Pentru cel deprins cu problemele, nu sunt necesare explicitări suplimentare; el ştie când este cazul, să se gândească şi la anumite aspecte implicite faţă de enunţ - de exemplu (dar poate că nu pentru stadiul gimnazial incipient) de ce 15 şi 30 de grade, sau poate β şi 2β? Cum s-ar exprima în general, unghiul dintre mediana şi înălţimea dintr-un acelaşi vârf?

Rezolvarea de probleme nu are ca scop satisfacerea temei primite pentru acasă… Dacă tot rezolvând problemă după problemă nu obţii şi deprinderea de a pune tu însuţi întrebări sau probleme - atunci culegerea respectivă şi întreg contextul şcolar aferent n-au reuşit să creeze nici o perspectivă reală şi nu prea au urmări (afară de note mari şi diplome şcolare). De aceea, o culegere de probleme - mai ales pentru nivelul incipient - ar trebui să fie ceva mai mult decât o grupare de enumerări indexate de enunţuri independente.

Modelarea problemei folosind GeoGebra

Lansăm GeoGebra, redimensionăm şi poziţionăm convenabil fereastra pe "desktop" şi lansăm recordmydesktop de pe linia de comandă:

recordmydesktop -x 0 -y 30 --width 570 --height 300 \
                --no-sound --overwrite --fps 25 \
                -o o15-30.ogv

S-a precizat colţul stânga-sus (0, 30), lăţimea şi înălţimea ferestrei de captat, s-a optat pentru "no-sound" (înregistrarea audio ocupă vreun MB, chiar dacă microfonul nu este folosit), s-a prevăzut frecvenţa de înregistrare (25 cadre/secundă) şi s-a numit fişierul .ogv rezultat.

Operăm cele necesare în fereastra lui GeoGebra şi în final, reintrăm în Terminal şi tastăm CTRL + C pentru terminarea înregistrării.

Redăm screencast-ul rezultat pentru modelarea problemei puse mai sus:

Constatăm că răspunsul trebuie să fie: "unghiul medianei cu înălţimea este de 45°"; cum putem demonstra aceasta?

Spectacolul rezolvării

Rezolvarea de probleme mai are (ar trebui să aibă) două scopuri importante: formularea deprinderii de a căuta şi a formula "idei de lucru", urmând să o tratăm efectiv pe aceea care pare cea mai potrivită; apoi, e vorba de… scrierea soluţiei (desigur, pentru acele probleme care merită acest efort).

Redactarea soluţiei este cu siguranţă aspectul cel mai neglijat (cel mai prost înţeles) în practica şcolară generală. Dar trebuie să fie clar, să nu ne păcălim: dacă ai rezolvat problema, dar nu eşti în stare să formulezi în scris rezolvarea - în mod coerent, cursiv, fără scăpări şi bineînţeles, fără greşeli de limbă (oricare ar fi această limbă) - atunci sigur, lipseşte ceva important din formaţia proprie actuală (şi - între altele - nu poţi pretinde mai mult de maximum 9).

Revenind la problema noastră, prima idee de lucru: să încercăm să arătăm că paralela prin piciorul înălţimii la mediană bisectează unghiul drept respectiv. "Defectul" acestei idei de lucru ar fi acela că ne-am concentra numai pe "partea dreaptă" a figurii (cum vom mai putea implica situaţia de mediană în "triunghiul mare"?).

A doua idee o repetă în fond pe prima enunţată, dar cu deosebirea esenţială că angajează întreaga figură: prin piciorul medianei ducem paralela la înălţime şi încercăm să dovedim că mediana iniţială este bisectoarea unghiului drept format:

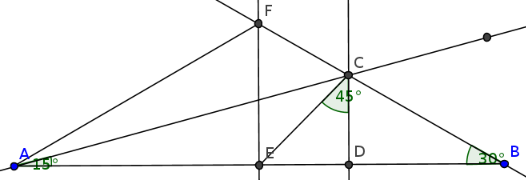
Triunghiul AFB este isoscel (fiindcă FE este şi mediană şi înălţime), deci unghiul său din A are 30°; rezultă că AC este bisectoare.

Teorema bisectoarei ne dă BC / CF = AB / AF. Dar AF = BF, AB = 2 BE şi în plus - dat fiind că EF este "cateta opusă unghiului de 30°" - avem BF = 2 EF; după înlocuiri şi simplificări obţinem BC / CF = EB / EF - adică EC este bisectoarea unghiului drept BEF. Cum triunghiul EDC este şi el dreptunghic, rezultă că unghiul ECD are 45° şi demonstraţia este încheiată.

Să observăm că nu prea este cazul vreunei generalizări, privitor la unghiurile de la bază - dat fiind că este implicată în mod esenţial "cateta opusă unghiului de 30°".

Reflectând CD faţă de EF, ajungem şi la această Observaţie (care întregeşte scena):
într-un triunghi isoscel care are la bază unghiuri de câte 30° dreptele care unesc mijlocul bazei cu picioarele bisectoarelor unghiurilor de la bază sunt perpendiculare.

Această Observaţie ridică la nivel de "teoremă" enunţul iniţial; dar ca "problemă" ar fi categoric mult mai slabă decât enunţul iniţial - pentru că vizează din start "întreaga figură" (şi mai mult - indică din start că este vorba de "bisectoare"), pe când formularea iniţială obligă la un anumit proces creativ de completare a figurii.

Întregul spectacol - logica de dorit pentru rezolvarea problemei, "de nota 10" - trebuie să angajeze unidirecţional: enunţul iniţial --> "întregirea figurii" şi raţionamentul aferent --> Observaţia finală enunţată mai sus (sau poate o alta, de luat în seamă).