Soluţie

Se întâmplă că n-am observat factorul `bb 3` din membrul drept şi am calculat mecanic:

Bineînţeles că "rezultatul" acestui calcul este imposibil (`a, b, c` fiind distincte). Aşa că am recitit enunţul, observând acum şi factorul `3` pe care îl omisesem iniţial… Dar - graţie acestei omisiuni şi calculului făcut mai sus - soluţia este acum clară: trecem un `(a-b)(b-c)` în primul membru, reducând egalitatea din enunţ la:

ceea ce echivalează cu `bb(2b = a + c)`, adică egalitatea dată are loc dacă şi numai dacă `a, b, c` sunt în progresie aritmetică.

Altă soluţie (mai simplă)

Cum aş fi rezolvat, dacă n-aş fi avut norocul să observ cele de mai sus?

Derivăm în raport cu `a` egalitatea dată, obţinând:

şi neglijând un multiplu de 2, avem `2b = a + c` încheind imediat "demonstraţia".

Altă "soluţie"

Probabil că propunătorul problemei (pentru Olimpiadă, "etapa locală", cl. a IX-a) a vizat soluţionarea "cea mai simplă", absolut mecanică: se trece totul în primul membru şi se fac toate înmulţirile şi reducerile de termeni asemenea, observând apoi că se obţine dezvoltarea la pătrat a expresiei `2b - a - c`. În fond - este aceeaşi soluţie ca prima, dar… mai contează şi cum prezinţi lucrurile.

Iar dacă de calcul "mecanic" este vorba, atunci putem folosi un pachet-soft destinat calculului simbolic. De exemplu, în consola SymPy Live putem introduce direct:

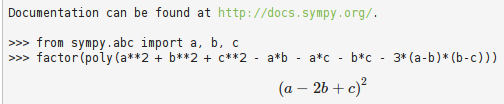
şi vedem imediat rezultatul descompunerii în factori a diferenţei membrilor egalităţii din enunţ.

Sau, având instalată biblioteca SymPy - putem lansa interpretorul Python într-un Terminal, căpătând libertatea de a investiga cât dorim lucrurile:

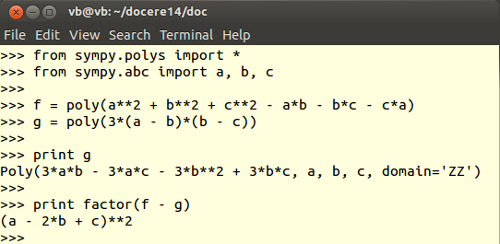
Din expresia afişată pentru g, vedem că poly() (importată din modulul sympy.polys) a construit polinomul Poly() pe baza expresiei furnizate (şi a "simbolurilor" a, b, c importate anterior), considerând coeficienţii în domeniul întregilor.

Relevanţă - pro şi contra

Ce spune problema, "din punct de vedere matematic"?
Spune cum să caracterizăm faptul că trei numere constituie o progresie aritmetică: printr-o egalitate de forma `a^2 + b^2 + c^2 - ab - bc - ca = 3(a - b)(b - c)`.

Dar cu siguranţă - nu vom folosi niciodată această caracterizare, în locul celei decente: `2b = a + c`.

Problema respectivă are meritele ei, legate de contextul concret în care există ca "problemă" (servind pentru testarea anumitor abilităţi ale elevilor); dar în sens matematic ea este complet irelevantă.

Abundenţa de "probleme propuse" irelevante cu care ne-a obişnuit învăţământul nostru conduce inevitabil la deformarea şi artificializarea perceperii lucrurilor; în realitate, ştiinţele nu se ocupă cu chestiuni irelevante, nici cu "chiţibuşuri" şi nici cu chiţibuşerii.

Să şi observăm (chiar credem că nu greşim) că odată intrat într-un sistem universitar (cu dorinţa de a studia o ştiinţă sau alta) - aproape că abandonezi "probleme propuse" şi începi să vezi adevăratul spirit al lucrurilor (şi până la urmă, adevăratele probleme); este drept că obişnuit cu amalgamul de "probleme propuse" la care vei fi aderat anterior, vor fi multe lucruri de îndreptat.

Lipsa de relevanţă (în absenţa implicării directe în contextul extern al problemei) - poate fi o "primă" cauză a neatenţiei petrecute la prima citire a enunţului…

Neglijarea constantelor - pro şi contra

Totuşi - cum de am omis iniţial factorul `3` (nu ne întrebăm mereu de ce se întâmplă una sau alta?)…

În fond, ce am făcut - am neglijat (voit sau nu) o constantă. Ori neglijarea factorilor constanţi din diverse expresii - în mod temporar, desigur - se practică în multe calcule sau raţionamente.

Ca să dăm un exemplu simplu, când avem de calculat o integrală ca `int 1/((x-1)(x-2)(x-3)) dx` vedem imediat că vom obţine o combinaţie liniară a logaritmilor factorilor de la numitor, urmând doar să mai determinăm parametrii acesteia.

Desigur, "neglijarea constantelor" nu trebuie să devină un obicei; aici, în problema prezentată mai sus - s-a întâmplat că efectul omisiunii (involuntare) a fost unul favorabil, dar în alte cazuri se poate ca efectul neglijării să fie unul nedorit.

Neglijarea constantelor nu trebuie să devină un obicei inconştient, cu atât mai mult cu cât - trebuie să recunoaştem - "constantele" ne guvernează întreaga existenţă!

Ne familiarizăm treptat pe parcursul şcolirii cu bazele diverselor ştiinţe - acele valori definitiv constituite şi universal acceptate ca fundament al evoluţiei ştiinţelor respective.

Dar cum stau lucrurile în învâţământul preuniversitar, în cazul ştiinţei "informatică"? Ce "constante" sunt vizate? Fără îndoială, "gândirea algoritmică" este just poziţionată ca fundament - studiindu-se algoritmii elementari de bază (la profilul "matematică-informatică"); trecem aici peste încadrări (n-ar fi ceva specific informaticii; la fel de bine - "face parte" din matematică), cât şi peste faptul că se abuzează de "probleme" irelevante şi - "în plus" faţă de matematică - mai apar acum (mai ales la "Olimpiadă") şi formulările puerile, deformând complet domeniul.

Dar ce instrumente sunt instituite, pentru studiul şi implementarea acestor algoritmi? Constatăm că se apelează constant la IDE-uri - deformând complet însăşi noţiunea de "program"; se ajunge până la a "înţelege" că execuţia programului decurge aşa: lansezi IDE-ul respectiv, încarci din meniul "Open" fişierul dorit şi tastezi o combinaţie de taste (ca CTRL+F9).

Învăţământul nostru s-a înglodat în produsele "point-and-click" şi în IDE-uri, creând între alte direcţionări eronate şi pe aceea că "informatica" înseamnă produsele Microsoft-Office şi platforma comercială Microsoft-Windows - limitând pe fiecare la desktop-ul propriu, la imprimantă şi la nivelul comercial "point-and-click" (şi străduindu-se să ne limiteze la nivelul comercial).

Nu credem să existe vreun produs informatic valoros - implementări de limbaje de programare, browsere, web-servere, editoare de text, chiar IDE-uri, etc. - care să fi fost realizat folosind vreun IDE, cum se instituie ca "bază" în învăţământul nostru…

Care sunt "constantele" reale de avut în vedere? De peste tot (dar cu excepţia învăţământului nostru!) rezultă că pentru realizarea produselor informatice sunt angajate - în mod constant şi în general fără restricţii comerciale - trei categorii de instrumente: terminal, editor de cod-sursă şi - după caz - compilator, sau interpretor pentru limbajul respectiv.

"Terminalul" serveşte de exemplu pentru crearea structurii de fişiere necesare şi pentru lansarea diverselor programe; editorul de cod-sursă serveşte desigur, pentru scrierea programelor în fişierele create (oferind eventual, facilităţi corespunzătoare); în final, se lansează de pe linia de comandă compilatorul sau interpretorul corespunzător, furnizându-i ca parametri fişierele-sursă constituite. Compilatorul lansat astfel produce programul executabil corespunzător, iar acesta poate fi pus în execuţie invocându-l de pe linia de comandă, sau eventual invocându-l dintr-un alt program (poate chiar şi "de la distanţă", de pe un alt calculator, cu respectarea anumitor protocoale).

Aşa se procedează cel mai adesea - indiferent de limbajele folosite, indiferent de genul de aplicaţie care trebuie dezvoltată şi oarecum indiferent de sistemul de operare subiacent; "oarecum" - fiindcă Windows-ul nu oferă nimic programatorului (să zicem "merci" că încă există interpretorul CMD.exe) şi trebuie căutate şi instalate clone de compilatoare şi interpretoare existente pe Linux.

În pofida acestei evidenţe, învăţământul nostru rămâne cantonat în sfera îngustă a produselor "point-and-click" - omiţând tocmai aceste instrumente fundamentale şi universale, pe care se bazează şi astăzi productivitatea şi libertatea specifice domeniului; iar această omisiune (care pare voită sau impusă), înseamnă din ce în ce mai mult "rămânere în urmă".