Un set de date URÂT: rezultatele bacalaureatului (II: statistici şi interpretări)
6. Notele finale versus instituţia contestaţiei
În tabelul original, notele acordate în urma soluţionării contestaţiilor sunt înregistrate separat de notele iniţiale. Dar se cuvine să avem încredere în "instituţia contestaţiei", încât până la urmă vom unifica aici coloanele respective (presupunând că proporţia litigiilor n-a ajuns la o limită care să sugereze repetarea întregului examen); desigur, nu de "încredere" este vorba, ci de faptul că în statisticile noastre interesează notele finale, nu şi cele iniţiale şi cele acordate la contestaţii.
În structura de date "bac5", coloanele notelor de la contestaţii au rangurile 23:26 şi conţin fie notele acordate de "Comisia de contestaţii", fie valoarea 'NA' (pentru absenţa contestaţiei); aplicăm fiecărei coloane 'q' dintre acestea, o funcţie anonimă care angajează funcţia is.na() pentru a verifica dacă valoarea curentă este sau nu 'NA' ("Not Available") şi funcţia sum(), care converteşte valorile logice la 0 şi 1 şi le însumează - rezultând numărul de contestaţii la proba respectivă:
> apply(bac5[, 23:26], 2, function(q) sum(!is.na(q))) -> frecvenţă_contestaţii > round(frecvenţă_contestaţii / nrow(bac5), 3) nota.A.co nota.B.co nota.C.co nota.D.co 0.134 0.003 0.078 0.084
La proba A au fost de aproape două ori mai multe contestaţii decât la C, sau la D - validând supoziţia larg acceptată că o lucrare la "Limba română" are mult mai mari şanse să fie notată sensibil diferit de către un alt corector, decât una la "Matematică". Dar altfel, având sub 15% contestaţii la o probă sau alta - nu credem că merită să ne mai ocupăm de contestaţii; vom elimina cele patru coloane, după ce determinăm întâi notele finale.
După normele oficiale actuale, nota finală este cea acordată de către comisia de contestaţii dacă nota iniţială este între 4.5 şi 4.99 (inclusiv), sau dacă nota iniţială este cel puţin 9.5, sau dacă diferenţa dintre cele două note este cel puţin 0.5; altfel, nota finală rămâne cea acordată iniţial:
noteFinale <- function() { for(k in 19:22) { # 'proba.A' este pe coloana 19, 'proba.B' pe 20, etc. ni <- bac5[, k] # notele iniţiale (sau '-2', '-1', 'NA') la proba indicată de k nc <- bac5[, k+4] # notele din contestaţie (sau 'NA') pentru proba indicată de k sch <- !is.na(ni) & !is.na(nc) & # schimbă (TRUE) sau nu, vechea notă cu cea nouă (ni >= 4.5 & ni < 5 | ni >= 9.5 | abs(ni - nc) >= 0.5) bac5[, k] <<- ifelse(sch, nc, ni) # "<<-" modifică variabilele "globale" } }
Pentru fiecare probă, am extras din "bac5" vectorul notelor iniţiale şi vectorul notelor din contestaţie şi am constituit vectorul de valori logice 'sch', astfel încât TRUE pe un anumit rang în acest vector să însemne că sunt îndeplinite condiţiile pentru schimbarea notei iniţiale cu cea de la contestaţie (pentru proba respectivă, la candidatul de pe rangul respectiv). Funcţia ifelse() primeşte ca argumente cei trei vectori şi returnează un vector care pe fiecare rang are fie valoarea din al doilea, fie pe cea din al treilea argument, în funcţie de valoarea logică de pe rangul respectiv din primul argument.
Am ambalat comenzile tocmai descrise într-o funcţie numai pentru a le refolosi cât mai simplu posibil, într-o procedură următoare de testare. În principiu, în R funcţiile nu au efecte laterale; dacă avem de modificat o variabilă "globală" (exterioră contextului funcţiei), atunci trebuie folosit operatorul "<<-" (vezi ultima linie din corpul funcţiei de mai sus).
Salvăm datele iniţiale, invocăm funcţia de mai sus pentru finalizarea notelor şi "ştergem" coloanele notelor acordate de comisia de contestaţii:
save(bac5, file="bac5.RData") # în vederea eventualei recuperări a datelor iniţiale noteFinale() # schimbă după caz, notele iniţiale cu cele din contestaţii bac5[, c(23:26)] <- NULL # elimină coloanele notelor acordate la contestaţii
Valorile negative -1 şi -2 care apar uneori în coloanele notelor iniţiale (rămânând nemodificate după secvenţa de mai sus), corespund cu "eliminat" sau "absent" şi dacă ar fi existat consecvenţă în această asociere, atunci puteam renunţa şi la câmpul "STATUS" (dar nu este cazul - de exemplu, întâlnim "-2" şi pentru "absent", dar şi în cazuri de "eliminat").
7. Procedură de testare
Aplicând o secvenţă de comenzi pe un lot voluminos de date - cum am făcut mai sus - apare imboldul imperios de a ne încredinţa că rezultatele sunt corecte. Putem proceda analog cu maniera standard de verificare a obiectelor produse într-o fabrică: nu se testează toate cele 10000 de becuri, ci doar 100 de becuri (sau poate numai 10) alese la întâmplare.
În secvenţa următoare - înscrisă în fişierul "check.R" - recuperăm "bac5" din fişierul "bac5.RData", extragem înregistrările care conţin cel puţin o contestaţie şi selectăm aleatoriu câteva dintre acestea; apoi transformăm setul "bac5" aplicându-i secvenţa de comenzi noteFinale() şi selectăm după aceea înregistrările corespunzătoare valorilor din câmpul Cand din lotul extras anterior:
1 2 3 4 5 6 7 8 | |
Avem de explicat unele dintre comenzile implicate aici; dar mai întâi - iată rezultatul produs:
> source("check.R") # execută în sesiunea R curentă, comenzile din fişier
Cand nota.A nota.B nota.C nota.D nota.A.co nota.B.co nota.C.co nota.D.co
46685 5.90 NA 5.80 5.80 NA NA NA 5.50
84923 5.00 NA 3.45 3.65 NA NA 3.6 3.60
224926 8.20 NA 9.90 8.30 9.1 NA NA 9.25
241672 8.60 NA 6.95 7.50 9.1 NA 7.5 7.15
351099 5.55 NA 5.50 6.55 4.5 NA 6.2 6.85
Cand nota.A nota.B nota.C nota.D
46685 5.9 NA 5.80 5.80
84923 5.0 NA 3.45 3.65
224926 9.1 NA 9.90 9.25
241672 9.1 NA 7.50 7.50
351099 4.5 NA 6.20 6.55
Primul lot de 5 linii de date prezintă notele iniţiale şi pe cele din contestaţii, iar al doilea prezintă notele finale corespunzătoare. Se poate vedea uşor că rezultatele sunt corecte; de exemplu, nota 4.5 din nota.A.co a devenit nota finală a probei A la candidatul identificat prin Cand=351099 (înlocuind nota iniţială 5.55) - în schimb, la acelaşi candidat, nota finală pentru proba D a rămas nota iniţială, fiindcă diferenţa dintre aceasta (6.55) şi nota din contestaţie (6.85) este sub 0.5.
În linia 3 avem o formulare funcţională concisă pentru ceea ce puteam exprima direct astfel:
litigii <- subset(bac5, !is.na(nota.A.co) | !is.na(nota.B.co) | !is.na(nota.C.co) | !is.na(nota.D.co))
Între cele două formulări avem cam aceeaşi diferenţă ca între scrierea termen cu termen a unei sume şi scrierea sumei respective folosind operatorul ∑. În loc de a scrie fiecare vector nota.*.co, împreună de fiecare dată cu !is.na(*) şi cu disjuncţia finală între ei - am considerat lista de vectori bac5[23:26], pe care (invocând sapply()) am aplicat funcţia is.na(); am obţinut astfel o matrice de valori logice pe care imediat le-am inversat aplicându-i operatorul '!' (negaţia logică vectorială); apoi, am transformat această matrice (invocând data.frame()) într-o listă de vectori coloană - listă pe care am transmis-o funcţiei Reduce(): aceasta va aplica operatorul primit '|' primilor doi vectori din listă, apoi vectorului rezultat şi următorului vector din listă, ş.a.m.d. până la epuizarea listei primite ca argument (a vedea eventual şi Două exemple de reducere/acumulare funcţională). Vectorul final rezultat astfel (cu atâtea valori logice câte linii are "bac5") a fost folosit apoi ca "vector-index", selectând în variabila "litigii" acele înregistrări din "bac5" cărora vectorul respectiv le asociază valoarea TRUE.
În linia 4 am invocat sample() pentru a selecta aleatoriu 5 înregistrări dintre cele existente în "litigii", păstrând numai câmpul de identificare "Cand" şi câmpurile notelor iniţiale şi ale celor de la contestaţii; în linia 5 am ordonat după câmpul "Cand" şi am afişat lotul respectiv.
Desigur, în numai 5 înregistrări s-ar putea să nu apară toate situaţiile posibile (de exemplu, în lotul redat mai sus nu apare cazul când nota iniţială este între 4.5 şi 4.99, nici cazul "≥ 9.5"); dar repetând execuţia secvenţei redate mai sus obţinem alte 5 înregistrări şi după două-trei repetări întâlnim de obicei mai toate cazurile (şi nici "5" nu-i bătut în cuie… am ales 5 fiindcă un lot de numai cinci înregistrări este uşor de analizat din ochi).
8. Învăţământul nostru difuzează mult prea multe "specializări"!
Tabelul CSV de la care am plecat (vezi [1]) avea 52 de coloane; multe serveau unor cerinţe de monitorizare (de exemplu, coloana "CONTESTATIE_EA" servea pentru a marca cererile de recorectare la proba A) şi deja le-am eliminat, nefiind utile pentru analiza statistică a rezultatelor.
Listăm numele şi indecşii câmpurilor (numite şi variabile, sau coloane) din "bac5" (cu menţiunea că faţă de [1] am simplificat denumirile coloanelor 15:18):
> names(bac5)
[1] "Cand" "Sex" "Specie" "Profil" "Filiera" "Forma"
[7] "Mediu" "proba.A" "proba.B" "limba" "proba.C" "proba.D"
[13] "Promoție" "ITA" "ITC" "PMS" "PMO" "IO"
[19] "nota.A" "nota.B" "nota.C" "nota.D" "DIGITALE" "STATUS"
[25] "Medie" "jud"
Folosind numele sau indecşii, putem grupa variabilele cum dorim; de exemplu, bac5[ c(24, 5) ] este o structură de tip "data.frame" care conţine numai coloanele "STATUS" şi respectiv "Filiera" din "bac5" şi care putea fi exprimată mai clar - dar… mai lung - prin bac5[ c("STATUS", "Filiera") ]. Expunem o înregistrare (are numărul de ordine 78183), pentru a sugera conţinutul câmpurilor:
> t(bac5[sample(1:nrow(bac5), 1), ]) # extrage aleatoriu (şi transpune) o înregistrare 78183 Cand "256596" ITA "B2" Sex "F" ITC "B2" # în loc de SCRIS_ITC Specie "Liceu cu program sportiv" PMS "B1" # în loc de SCRIS_PMS Profil "Educație fizică și sport" PMO "B2" # în loc de ORAL_PMO Filiera "Vocationala" IO "B2" # în loc de ORAL_IO Forma "Zi" nota.A "7" Mediu "URBAN" nota.B NA proba.A "Limba română (REAL)" nota.C "5" proba.B "" nota.D "6.1" limba "Limba engleză" DIGITALE "18" proba.C "Istorie" STATUS "Promovat" proba.D "Geografie" Medie "6.03" Promoție "2014-2015" jud "Gorj"
Datele care ne-au rămas din tabelul iniţial, în structura de date "bac5", sunt suficiente (ba chiar - încă sunt prea multe!) pentru a elabora o analiză statistică de un nivel onorabil, a rezultatelor examenului. Sunt "prea multe", în sensul că unele atribute prezintă prea multe ramificaţii care mai degrabă sunt "neimportante" din punct de vedere statistic; de exemplu, "Specie" ramifică înregistrările (candidaţii) pe 96 de "specializări" - ceea ce este excesiv de amănunţit:
> table(bac5$Specie) -> spec # frecvenţa specializărilor > print(as.data.frame(sort(spec)), row.names=FALSE) Var1 Freq Bibliotecar documentarist 1 # ... urmează încă 2 "specializări" cu câte o singură înregistrare; apoi: Instructor pentru activități extrașcolare 11 # ... încă 45 "specializări" cu câte între 12 şi 314 înregistrări; apoi: Matematica-informatica 317 Tehnician instalator pentru construcții 317 # ... încă 37 "specializări" cu câte între 390 şi 3332 înregistrări; apoi: Tehnician ecolog și protecția calității mediului 3985 Liceu cu program sportiv 4493 Tehnician în turism 5226 # 3% din total Științe Sociale 11686 Tehnician în activități economice 12259 Științe ale Naturii 20376 Filologie 23768 Matematica-Informatica 32268
Statistica nu se ocupă de o singură înregistrare (cazul primelor trei "specializări" listate mai sus), ba chiar ignoră pe cât de poate, subseturile de proporţie neglijabilă; din tabelul de frecvenţe redat parţial mai sus rezultă că mai mult de 80% dintre candidaţi au "specializarea" acoperită de numai 16 dintre cele 96 de valori indicate pentru "Specie":
> subset( as.data.frame(spec), Freq > 2000 ) -> spec2000
> cat( nrow(spec2000), " specializări = ", sum(spec2000[, 2])/nrow(bac5), "%\n" )
16 specializări = 0.8053203 %
Şi de fapt trebuiau să fie nu 96, ci 95 de specializări: specializarea "Matematică Informatică" apare o dată ca "Matematica-informatica" pentru 317 candidaţi şi apoi ca "Matematica-Informatica" pentru 32268 candidaţi (greşeală de scriere specifică lucrului în Excel la nivelul de editare manuală a tabelului); cele două apariţii corespund indexului 14:15 în vectorul nivelelor factorului "Specie" şi le putem reuni astfel:
> levels(bac5$Specie)[14:15] # inspectează [1] "Matematica-informatica" "Matematica-Informatica" > levels(bac5$Specie)[14:15] <- "Matematică-Informatică" # comasează şi redenumeşte
Recalculând după această corectură frecvenţele specializărilor, vom obţine acum pe ultimul rând din listingul redat mai sus, "Matematică-Informatică 32585" (din 32268 + 317).
Până la micul experiment statistic expus mai sus, n-am conştientizat faptul că avem aşa de multe "specializări"; totuşi, 95 chiar sunt mult prea multe, măcar pentru motivul statistic evidenţiat mai sus, că marea majoritate a elevilor (80% din serie) acoperă numai 16 dintre acestea.
9. Ce spun datele?
Rezultatele examenului apar în coloanele "STATUS" şi "Medie" (de indecşi 24 şi 25 - vezi vectorul numelor variabilelor de la §8); dacă elevul a absentat la o probă, sau a fost eliminat din examen, atunci în coloana 24 avem valoarea "Absent", respectiv "Eliminat" - iar altfel, valorile acestor două variabile (numite "variabile dependente", sau "calculate") se determină pe baza valorilor înregistrate în coloanele 19-22 (numite variabile "independente").
Este drept că tot "rezultate" trebuie considerate şi coloanele 14-18 şi 23, pe care s-au înregistrat direct nivelele de competenţe lingvistice şi digitale; desigur, coloanele 14-18 (vezi înregistrarea exemplificată la §8) ar putea fi înlocuite printr-o singură coloană, având valori şiruri de caractere formate după şablonul "B2 B2 B1 B2 B2".
Coloanele 2-13 şi 26 reprezintă diverse atribute ale candidaţilor, sau ale notelor din coloanele 19-22 - permiţând diverse grupări şi clasificări ale rezultatelor. De exemplu, putem investiga repartiţia rezultatelor după Sex şi Mediu, sau după filieră, sau după judeţ - etc.
9.1. Sortimentul "Tehnologică" este păgubos ("STATUS" versus "Filiera")
Deja la §8 am văzut "ce spun" datele apropo de specializări: sunt de 5 ori mai multe decât s-ar cuveni pentru ca sistemul să rămână consistent. Cele 95 de "specializări" ţin de trei "filiere":
> levels(bac5$Filiera) # "Tehnologica" "Teoretica" "Vocationala" > levels(bac5$Filiera) <- c("Tehnologică", "Teoretică", "Vocaţională")
Bineînţeles că - fiind aşa de simplu de făcut, prin funcţia levels() - am corectat denumirile iniţiale de "filiere"; precizăm că în continuare vom omite promptul "> " când vom mai reda comenzile interactive pe care le folosim.
Funcţia table() produce un tabel de contingenţă: determină frecvenţa în cadrul setului de date, pentru fiecare combinaţie de nivele ale factorilor indicaţi; iar apoi, funcţia addmargins() adaugă tabelului totaluri marginale (însumând pe linii şi respectiv, pe coloane):
addmargins(table(bac5[c('STATUS', 'Filiera')])) -> STF Filiera STATUS Tehnologică Teoretică Vocaţională Sum Absent 6966 1922 335 9223 Eliminat 350 178 18 546 Nepromovat 31623 15470 3757 50850 Promovat 28360 70528 9432 108320 Sum 67299 88098 13542 168939
Împărţind toate valorile prin numărul de candidaţi, obţinem frecvenţele relative şi le exprimăm procentual (cu rotunjire la a doua zecimală):
nr <- STF[5, 4] # = 168939 (=nrow(bac5)) round(STF/nr*100, 2) # procente faţă de numărul total de candidaţi Filiera STATUS Tehnologică Teoretică Vocaţională Sum Absent 4.12 1.14 0.20 5.46 Eliminat 0.21 0.11 0.01 0.32 Nepromovat 18.72 9.16 2.22 30.10 Promovat 16.79 41.75 5.58 64.12 Sum 39.84 52.15 8.02 100.00
mosaicplot() transpune grafic liniile şi coloanele (excludem însă, marginile); aria fiecărui dreptunghi este proporţională cu frecvenţa categoriei reprezentate:
mosaicplot(STF[-5, -4], col=c(2:4), las=2, cex.axis=0.8, main="")
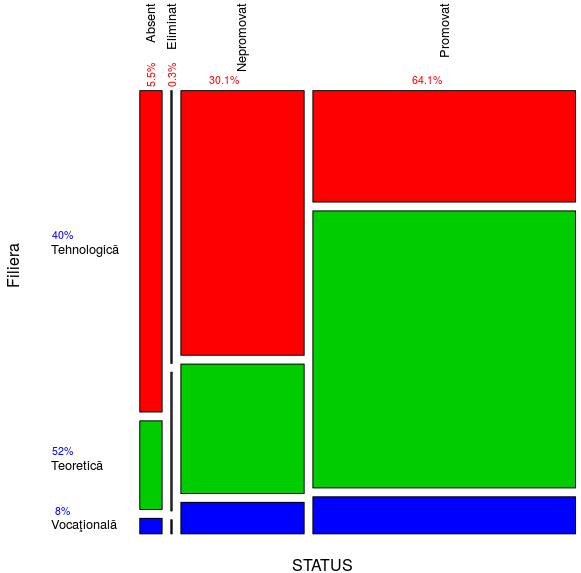
"col=c(2:4)" alege culorile de indecşi 2:4 din paleta standard, pentru zonele dreptunghiulare asociate celor trei filiere; "las=2" asigură scrierea numelor perpendicular pe axe. Am înscris pe grafic şi procentele marginale (rotunjite), folosind funcţia text() - de exemplu:
text(c(0), c(0.56, 0.13, 0.01), labels=c("40%", "52%", "8%"), cex=0.66, col="blue") text(0.17, 0.88, labels="5.5%", cex=0.66, col="red", srt=90)
srt=90 roteşte textul (indicat în parametrul "labels") cu 90°; prin "cex" se proporţionează mărimea de caracter a textului. Imaginea redată mai sus poate fi mărită: click-dreapta şi "View Image".
Între filiera "Tehnologică" şi celelalte două avem o discrepanţă care sare în ochi: culoarea roşie este covârşitoare pe dreptunghiurile stărilor "Absent" şi "Nepromovat" (la fel şi pentru "Eliminat"), cu toate că proporţia ei în cadrul întregii populaţii este doar 40%. Făcând raportul dintre liniile numite "Promovat" şi "Sum" (a 4-a şi a 5-a linie) din tabelul frecvenţelor absolute redat mai sus, obţinem proporţia de promovaţi din cadrul fiecărei filiere:
round(STF[4, ] / STF[5, ] *100, 2) # nr. promovaţi / volum Filieră (*100) Tehnologică Teoretică Vocaţională Sum 42.14 80.06 69.65 64.12
Pe filiera "Tehnologică" procentul de respinşi este cu aproape 8% mai mare decât procentul de promovaţi, în timp ce la celelalte filiere procentul de respinşi este mult sub cel de promovaţi. N-ar fi greşit să concluzionăm că filiera "Tehnologică" - aşa cum este ea organizată şi structurată până în prezent - nu-şi justifică existenţa, în cadrul sistemului de învăţământ liceal (încheiat cu "examen de bacalaureat"); avem o analogie mai mult sau mai puţin forţată (dar astfel de analogii fac parte acum din discursul oficial obişnuit): ce face un manager când vede că unul dintre produse nu se vinde? - de obicei, se gândeşte să excludă sortimentul din cauza căruia iese în pierdere.
9.2. "STATUS" versus un criteriu de clasificare oarecare
Putem generaliza analiza din §9.1 pentru oricare alt factor existent sau adăugat în structura de date "bac5", prin funcţia următoare:
status_vs <- function(field) { # numele câmpului (de clasă "factor") addmargins(table(bac5[c('STATUS', field)])) -> status mosaicplot(status[-nrow(status), -ncol(status)], # exclude totalurile marginale col=TRUE, las=2, cex.axis=0.8, main="") return(round(status/nrow(bac5)*100, 3)) }
De exemplu, reobţinem tabelul de contingenţă şi graficul de la §9.1 prin comanda:
> status_vs("Filiera")
Poate ar fi interesante repartiţiile după "Sex", respectiv după "Mediu":
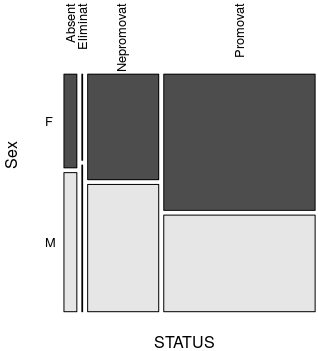
> status_vs("Sex") Sex STATUS F M Sum Absent 2.197 3.263 5.459 Eliminat 0.120 0.204 0.323 Nepromovat 13.639 16.461 30.100 Promovat 37.509 26.609 64.118 Sum 53.464 46.536 100.000
> status_vs("Mediu") Mediu STATUS RURAL URBAN Sum Absent 2.381 3.079 5.459 Eliminat 0.182 0.141 0.323 Nepromovat 12.162 17.938 30.100 Promovat 15.850 48.268 64.118 Sum 30.574 69.426 100.000
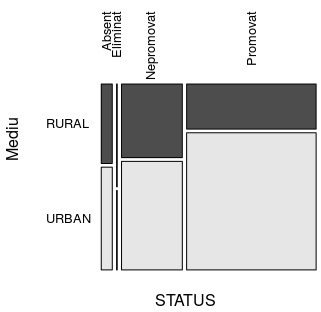
Dintre candidaţii de sex feminin au promovat 37.509 / 53.464 ≈ 70%, iar pentru sexul masculin avem doar 26.609 / 46.536 ≈ 57% promovaţi; putem semnala diferenţa (şi este mare), dar nu o putem explica. Analog, constatăm că procentul promovaţilor din rândul candidaţilor cu domiciliul în mediul rural este de 52% şi procentul promovaţilor din rândul celor domiciliaţi în mediul urban este de aproape 70% - iarăşi o diferenţă mare, care… se pretează la multe explicaţii.
Putem proceda la fel, pentru oricare alt criteriu de clasificare existent şi poate că am putea deduce nişte aspecte interesante pentru "proba.B", "proba.C", sau pentru "ITA", sau "ITC" etc.; însă de exemplu pentru "Forma" nu vom găsi nimic interesant, dat fiind că peste 97% dintre candidaţi provin de la forma de învăţământ "Zi" (şi putem ignora liniştit, "Frecvenţă redusă" şi "Seral").
Să înfiinţăm noi un criteriu de clasificare şi să folosim pentru acesta funcţia introdusă mai sus. Coloana bac5$DIGITALE înregistrează punctajele obţinute de candidaţi la proba de "competenţe digitale" - numere întregi 0..100 (dar şi valori NA); transformăm acest vector numeric într-un "factor" (folosind funcţia cut()), pe care îl adăugăm structurii de date "bac5":
bac5$Dig <- cut(bac5$DIGITALE, breaks=c(-1, 11, 31, 56, 75, 101), labels=c("fără", "încep", "mediu", "avans", "exper"), ordered_result=TRUE)
Intervalul (-1, 11) adică [0, 10] (inclusiv 0 şi 10) reprezintă nivelul numit "fără" al factorului tocmai creat, bac5$Dig (însemnând că pentru mai puţin de 11 puncte nu se va acorda nici un calificativ); intervalul de puncte [11, 30] corespunde nivelului "încep" (pentru calificativul de "începător"), ş.a.m.d. Aplicând funcţia definită mai sus obţinem:
> status_vs("Dig") Dig STATUS fără încep mediu avans exper Sum Absent 0.220 1.293 1.178 0.411 0.110 3.211 Eliminat 0.004 0.075 0.125 0.063 0.028 0.295 Nepromovat 0.803 8.272 12.187 5.019 1.409 27.689 Promovat 0.114 3.660 17.538 19.653 15.059 56.024 Sum 1.139 13.299 31.029 25.146 16.606 87.220
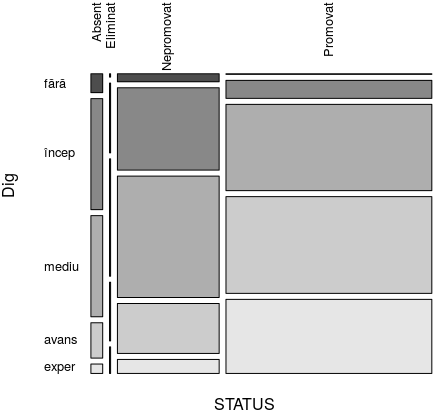
Faptul că suma finală este 87.22 şi nu 100 se explică prin aceea că în funcţia "status_vs()" am raportat în final prin nrow(bac5) (numărul tuturor candidaţilor), ori coloana bac5$DIGITALE conţinea şi valori NA - vedem acum că acestea sunt în procent de 100 - 87.22 = 12.18% - iar acestea sunt ignorate în funcţiile cut() şi table(). N-am vrut să înlocuiesc valorile respective cu 0 (de exemplu), fiindcă ele apar şi la unii promovaţi şi la unii nepromovaţi (putând însemna că a luat 0 puncte şi în final a promovat, dar la fel de bine - că nu s-a prezentat la proba respectivă).
Să recuperăm tabelul de mai sus şi să raportăm linia 4 ("Promovat") la linia 5 (totalul pe fiecare nivel de competenţă digitală):
> stdg <- status_vs("Dig") > round(stdg[4, ] / stdg[5, ]*100, 3) fără încep mediu avans exper Sum 10.009 27.521 56.521 78.156 90.684 64.233
Rezultatele se citesc desigur astfel: dintre cei care au primit 0..10 puncte la "DIGITALE", au promovat 10%; printre cei cu 11..30 puncte ("începător"), 27.52% sunt promovaţi; competenţa de nivel "mediu" a atins o promovabilitate de 56.52%; ş.a.m.d. Fiindcă şi nivelele de competenţă şi procentele de promovare corespunzătoare, apar în ordinea crescătoare (a punctajelor, respectiv a procentelor), putem concluziona că şansele de promovare cresc sensibil, odată cu nivelul de competenţă digitală (probabil era de aşteptat…).
9.3 Promovabilitatea pe judeţe ("STATUS" versus "jud")
Pentru un factor care are multe nivele (cum este "jud"), va fi mai clară o reprezentare grafică prin bare asociate nivelelor, decât cea de tip "mozaic" produsă prin funcţia de mai sus status_vs(): barele - câte 4 pentru fiecare judeţ, corespuzătoare nivelelor "STATUS" - au toate o aceeaşi lăţime (distincţiile fiind date de înălţimea barelor, spre deosebire de "mozaic" unde avem de perceput arii de dreptunghiuri).
Pe de altă parte (mai ales că "jud" are 42 de nivele) este de judecat dacă toate cele 4 situaţii "STATUS", merită să fie reprezentate; dacă ponderea celor eliminaţi este foarte mică, în majoritatea judeţelor - atunci am putea renunţa să mai reprezentăm bara "Eliminat".
Folosim iarăşi funcţia table() pentru a obţine tabelul de contingenţă pentru "jud" şi "STATUS", apoi prop.table() pentru a relativiza valorile respective faţă de numărul de candidaţi din fiecare judeţ şi în final - ordonăm liniile matricei obţinute după procentul de promovabilitate:
table(bac5[c('jud', 'STATUS')]) -> jud_status round(prop.table(jud_status, 1), 3) -> jud_sta ord_prom <- order(jud_sta[, 4]) jud_sta[ord_prom, ] -> jud_sta
> jud_sta # inspectăm rezultatul STATUS jud Absent Eliminat Nepromovat Promovat Giurgiu 0.066 0.002 0.583 0.348 Ilfov 0.096 0.001 0.524 0.378 Teleorman 0.091 0.003 0.504 0.403 Mehedinţi 0.087 0.000 0.411 0.502 Gorj 0.074 0.004 0.417 0.505 Harghita 0.062 0.001 0.413 0.524 Constanţa 0.066 0.004 0.402 0.528 Olt 0.088 0.001 0.382 0.529 Călăraşi 0.061 0.002 0.405 0.532 Arad 0.065 0.001 0.367 0.568 Caraş-Severin 0.087 0.003 0.343 0.568 Dolj 0.095 0.002 0.334 0.569 Dâmboviţa 0.054 0.001 0.361 0.584 Sălaj 0.072 0.001 0.341 0.586 Covasna 0.046 0.001 0.343 0.609 Timiş 0.061 0.029 0.300 0.610 Bihor 0.039 0.019 0.317 0.624 Vâlcea 0.057 0.001 0.317 0.625 Maramureş 0.068 0.002 0.293 0.638 Ialomiţa 0.063 0.002 0.291 0.644 Hunedoara 0.061 0.000 0.283 0.656 Argeş 0.034 0.001 0.304 0.661 Mureş 0.049 0.002 0.286 0.663 Vaslui 0.050 0.001 0.285 0.664 Bistriţa-Năsăud 0.069 0.000 0.264 0.667 Neamţ 0.048 0.021 0.263 0.668 Suceava 0.046 0.000 0.285 0.669 M.Bucureşti 0.043 0.001 0.283 0.672 Vrancea 0.048 0.000 0.272 0.679 Tulcea 0.068 0.000 0.249 0.683 Buzău 0.032 0.001 0.283 0.684 Botoşani 0.049 0.001 0.247 0.704 Satu-Mare 0.030 0.000 0.253 0.717 Alba 0.041 0.002 0.234 0.723 Prahova 0.043 0.001 0.234 0.723 Galaţi 0.045 0.001 0.224 0.729 Sibiu 0.059 0.001 0.210 0.731 Iaşi 0.057 0.001 0.210 0.732 Bacău 0.043 0.001 0.191 0.765 Braşov 0.034 0.001 0.187 0.778 Brăila 0.016 0.000 0.206 0.778 Cluj 0.026 0.000 0.161 0.813
În coloana "Eliminat" avem valori chiar neglijabile: aproape 3% în Timiş, 2% în Bihor şi Neamţ şi sub 0.4% în celelalte 39 de judeţe. Pentru "Absent", merită să vedem valorile statistice principale:
summary(jud_sta[, 1]) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.01600 0.04350 0.05700 0.05688 0.06750 0.09600
Jumătate dintre judeţe au procentul de absenţi între 4.35% (prima quartilă, "1st Qu.") şi 6.75% (a treia quartilă, "3st Qu."); cel mai mare procent de absenţi este 9.6% (judeţul Ilfov).
Am văzut mai sus că procentul de eliminaţi este nesemnificativ; pentru a vedea cât de semnificativ este procentul de absenţi, să-l raportăm la procentul de "Nepromovat":
jud_sta[, 1] / jud_sta[, 3] -> abs_nep # raportul între 'Absent' şi 'Nepromovat' summary(abs_nep) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.07767 0.15430 0.18020 0.18560 0.21460 0.28440
Prin urmare, absenteismul ar explica cel mult 3% din procentul celor respinşi - ceea ce înseamnă că putem simplifica fără îndoieli, lucrurile: vom viza numai statutul de "
"jud_sta" este o structură de date de clasă "table" (derivată în fond din "matrice"); o convertim la clasa "data.frame" (cum pretind de obicei funcţiile de reprezentare grafică prin bare):
class(jud_sta) [1] "table" as.data.frame(jud_sta) -> jud_sta_df str(jud_sta_df) # inspectăm structura de date 'data.frame': 168 obs. of 3 variables: $ jud : Factor w/ 42 levels "Giurgiu","Ilfov",..: 1 2 3 4 5 6 7 8 9 10 ... $ STATUS: Factor w/ 4 levels "Absent","Eliminat",..: 1 1 1 1 1 1 1 1 1 1 ... $ Freq : num 0.066 0.096 0.091 0.087 0.074 0.062 0.066 0.088 0.061 0.065 ...
Extragem numai înregistrările pentru "Promovat", excluzând desigur a doua coloană:
subset(jud_sta_df, STATUS=="Promovat", select=c(-2)) -> jud_prom
Putem sintetiza grafic datele astfel selectate, folosind funcţia ggplot() din pachetul ggplot2:
require(ggplot2) ggplot(jud_prom, aes(x=jud, y=Freq)) + geom_bar(stat='identity', col="white", fill="lightgreen", width=0.85) + labs(x="", y="", title="Bacalaureat 2015: proporţia promăvării, pe judeţe") + coord_flip()
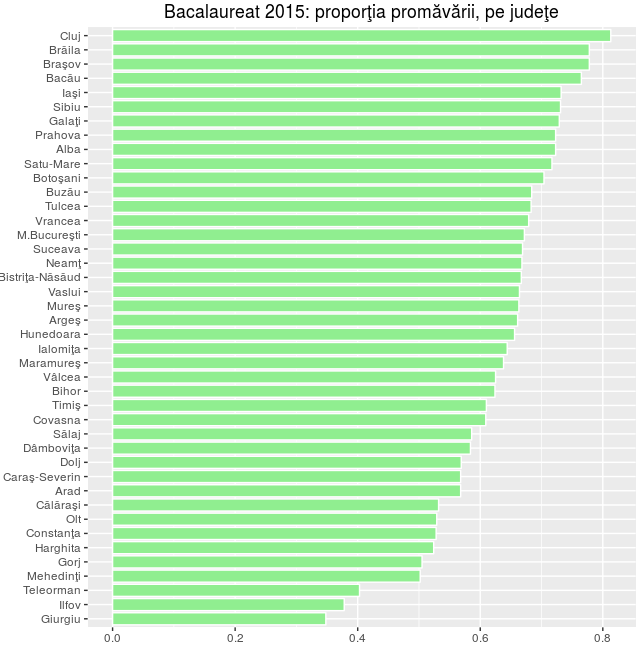
Să vedem şi statisticile principale:
summary(jud_prom$Freq) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.3480 0.5682 0.6585 0.6294 0.6990 0.8130
Valoarea medie a procentului de promovaţi pe judeţ este de aproape 63%; pentru jumătate dintre judeţe, procentul de promovaţi este cuprins între 56.8% şi 69.9%.
vezi Cărţile mele (de programare)