Un set de date URÂT: rezultatele bacalaureatului (IV: probe, note şi medii)
[1] Un set de date URÂT: rezultatele bacalaureatului (I: curăţarea datelor) (§1 - §5),
(II: statistici şi interpretări) (§6 - §9.3), (III: competenţe lingvistice) (§9.4),
[2] Statistici pe judeţ, mediu şi grupe de medii, folosind R (partea a II-a)
9.5 Probele scrise
Intenţionăm să ne ocupăm din punct de vedere statistic, de notele şi de mediile candidaţilor. Dar fiecare coloană de note corespunde la 2, 4, 10 sau chiar 18 obiecte de învăţământ; ne putem ocupa (din punct de vedere statistic) de fiecare obiect în parte - dar are sens aşa ceva?
Folosim iarăşi instrumentul lapply(), aplicând funcţia levels() fiecăreia dintre variabilele (de clasă "factor") corespunzătoare în "bac5" categoriilor de obiecte (probelor):
lapply(bac5[c(8:12)], levels) $proba.A # coloana 8 [1] "Limba română (REAL)" "Limba română (UMAN)" $proba.B # limba maternă (coloana 9) [1] "" "Limba croată" "Limba germană" [4] "Limba italiană" "Limba maghiară (REAL)" "Limba maghiară (UMAN)" [7] "Limba sârbă" "Limba slovacă" "Limba turcă" [10] "Limba ucraineană" $limba # limba străină - ţine de "competenţe lingvistice" (v. §9.4) [1] "Limba ebraică" "Limba engleză" "Limba franceză" [4] "Limba germană modernă" "Limba italiană" "Limba japoneză" [7] "Limba portugheză" "Limba rusă" "Limba spaniolă" [10] "Limba turcă modernă" $proba.C # coloana 11 [1] "Istorie" "Matematică MATE-INFO" "Matematică PED" [4] "Matematică ST-NAT" "Matematică TEHN" $proba.D # coloana 12 [1] "Anatomie și fiziologie umană. genetică și ecologie umană" [2] "Biologie vegetală și animală" [3] "Chimie anorganică TEH Nivel I/II " [4] "Chimie anorganică TEO Nivel I/II " [5] "Chimie organică TEH Nivel I/II" [6] "Chimie organică TEO Nivel I/II" [7] "Economie" [8] "Filosofie" [9] "Fizică TEH" [10] "Fizică TEO" [11] "Geografie" [12] "Informatică MI C/C++" [13] "Informatică MI Pascal" [14] "Informatică SN C/C++" [15] "Informatică SN Pascal" [16] "Logică. argumentare și comunicare" [17] "Psihologie" [18] "Sociologie"
Notele din coloana 'nota.A' (a 19-a din "bac5") corespund probei numite în mod standard "Limba şi literatura română"; însă factorul 'proba.A' separă notele respective în două secţiuni; am putea investiga în parte, fiecare secţiune - dar are sens această separare? Subiectele de rezolvat or fi ţinut ele cont de faptul că se adresează secţiunii 'REAL' şi respectiv 'UMAN', dar notele măsurate în final sunt în ambele cazuri, punctaje din intervalul [1, 10]; baremul după care se măsoară nota ţine cont desigur, de subiect (deci de secţiune), dar de fapt este cel corespunzător probei de "Limba română" (nu pentru "Matematică", sau altă probă).
Putem constata şi direct, că din punct de vedere statistic cele două secţiuni nu diferă semnificativ (având cam aceeaşi repartiţie a notelor):
bac5[bac5$proba.A == "Limba română (UMAN)", ] -> uman bac5[bac5$proba.A == "Limba română (REAL)", ] -> real summary(uman$nota.A) Min. 1st Qu. Median Mean 3rd Qu. Max. -2.000 5.900 7.450 7.016 8.500 10.000 summary(real$nota.A) Min. 1st Qu. Median Mean 3rd Qu. Max. -2.000 5.150 6.700 6.351 8.200 10.000
Nota minimă este "-2.000" (negativă) - am uitat de faptul că în coloanele de note avem şi valorile "-1" şi "-2" (pe lângă note obişnuite), semnificând "Absent" sau "Eliminat" (v. §.6); prin urmare, quartilele obţinute sunt ceva mai mici decât sunt în realitate (după ce vom fi exclus valorile negative). Oricum, se vede că diferenţele între cele două secţiuni (pe quartilele respective) sunt mai mici decât 1%.
Cu o secvenţă de comenzi similară celeia redate mai sus, putem obţine quartilele repartizării notelor pentru oricare dintre obiectele vizate de o probă sau alta. Ca şi în §9.4 putem obţine deasemenea, tabelul de contingenţă între probele respective (câţi candidaţi au susţinut cutare probe, alegând după caz cutare obiecte ale fiecăreia) - de exemplu:
table(bac5[c(8, 11, 12)]) -> scris.ctg # contingenţa probelor A, C şi D as.data.frame(scris.ctg) -> scris.df scris.df[scris.df$Freq != 0, ] -> scris.df # ignoră frecvenţa 0 str(scris.df) # inspectăm structura de date rezultată 'data.frame': 39 obs. of 4 variables: $ proba.A: Factor w/ 2 levels "Limba română (REAL)",..: 1 1 1 1 1 1 1 1 1 1 ... $ proba.C: Factor w/ 5 levels "Istorie","Matematică MATE-INFO",..: 2 4 5 2 ... $ proba.D: Factor w/ 18 levels "Anatomie și fiziologie umană. genetică și ecologie $ Freq : int 11742 12784 5101 6395 3808 28172 2264 885 609 711 ...
În acest exemplu, pentru cele trei probe avem 2×5×18 = 180 de combinaţii de obiecte ale acestora, dar îndepărtându-le pe cele de frecvenţă 0 (de exemplu, nu există niciun candidat cu "Limba română (REAL)" la prima probă, cu "Istorie" la a doua şi cu "Fizică TEO" la a treia probă) ne-au rămas 39 de înregistrări. Dacă vrem să afişăm rezultatele, putem folosi o funcţie precum abbreviate(), pentru a scurta denumirile obiectelor probei D:
levels(scris.df$proba.D) <- abbreviate(levels(scris.df$proba.D), minlength=20) print(scris.df[order(-scris.df$Freq), ], row.names=FALSE) proba.A proba.C proba.D Freq Limba română (REAL) Matematică TEHN Biologvegetalșanimal 28172 Limba română (REAL) Matematică TEHN Geografie 24967 Limba română (UMAN) Istorie Geografie 23139 Limba română (REAL) Matematică ST-NAT Antmșfzlgumngntcșecu 12784 Limba română (REAL) Matematică MATE-INFO Antmșfzlgumngntcșecu 11742 Limba română (REAL) Istorie Geografie 9445 Limba română (UMAN) Istorie Logicargumentrșcmncr 6496 Limba română (REAL) Matematică MATE-INFO Biologvegetalșanimal 6395 Limba română (REAL) Matematică MATE-INFO Informatică MI C/C++ 6029 Limba română (REAL) Matematică TEHN Antmșfzlgumngntcșecu 5101 Limba română (REAL) Matematică MATE-INFO Fizică TEO 4473 Limba română (REAL) Matematică ST-NAT Biologvegetalșanimal 3808 Limba română (UMAN) Istorie Sociologie 3457 Limba română (REAL) Matematică TEHN Fizică TEH 3144 Limba română (REAL) Matematică ST-NAT ChimorgancTEONvlI/II 2324 Limba română (REAL) Matematică TEHN ChimanrgncTEHNvlI/II 2264 Limba română (REAL) Matematică TEHN Logicargumentrșcmncr 1943 Limba română (REAL) Matematică MATE-INFO ChimorgancTEONvlI/II 1857 Limba română (UMAN) Matematică PED Geografie 1482 Limba română (REAL) Matematică MATE-INFO InformaticăMIPascal 1205 Limba română (REAL) Istorie Logicargumentrșcmncr 1143 Limba română (UMAN) Istorie Psihologie 1083 Limba română (REAL) Matematică MATE-INFO ChimanrgncTEONvlI/II 885 Limba română (UMAN) Istorie Economie 777 Limba română (REAL) Matematică TEHN ChimorgancTEHNvlI/II 711 Limba română (REAL) Matematică TEHN Economie 702 Limba română (REAL) Matematică ST-NAT Fizică TEO 701 Limba română (REAL) Matematică ST-NAT ChimanrgncTEONvlI/II 609 Limba română (UMAN) Istorie Filosofie 515 Limba română (UMAN) Matematică PED Logicargumentrșcmncr 444 Limba română (REAL) Matematică TEHN Psihologie 294 Limba română (REAL) Istorie Filosofie 267 Limba română (REAL) Istorie Psihologie 206 Limba română (UMAN) Matematică PED Psihologie 187 Limba română (REAL) Matematică ST-NAT Informatică SN C/C++ 135 Limba română (REAL) Istorie Economie 18 Limba română (REAL) Matematică ST-NAT InformaticăSNPascal 15 Limba română (UMAN) Matematică PED Economie 11 Limba română (UMAN) Matematică PED Filosofie 9
Iar acum putem extrage subtabele de contingenţă; de exemplu, dacă ne-ar interesa frecvenţa pe obiectele probei D între candidaţii de la "MATE-INFO":
subset(scris.df, proba.C=="Matematică MATE-INFO", select=c(3, 4)) proba.D Freq Antmșfzlgumngntcșecu 11742 # Anatomie și fiziologie umană. genetică și ecologie umană Biologvegetalșanimal 6395 Informatică MI C/C++ 6029 Fizică TEO 4473 ChimorgancTEONvlI/II 1857 InformaticăMIPascal 1205 ChimanrgncTEONvlI/II 885
Punctăm în treacăt, că proporţia celor de la "matematică-informatică" având "Anatomie" sau "Biologie" la proba D (primele două rânduri pe rezultatele redate mai sus) este de aproape trei ori mai mare decât pentru "Informatică" (linia 3 plus linia 6) - ceea ce ar trebui văzut că este cam pe dos de cum s-ar cuveni…
9.6 Clasificarea după nivelul notelor şi mediilor
Ne-am amintit ceva mai înainte, că în coloanele de note avem şi valori "-1" şi "-2"; înlocuim toate aceste valori prin "NA":
bac5[, 19:22][bac5[, 19:22] < 0] <- NA
Acum putem obţine corect, quartilele corespunzătoare notelor pe fiecare probă în parte şi pe cele corespunzătoare mediilor finale; aplicăm summary() coloanelor respective, folosind sapply() (care simplifică rezultatele produse de lapply(), formând o matrice a acestora):
sapply(bac5[c(19:22, 25)], summary) nota.A nota.B nota.C nota.D Medie Min. 1.000 1.300 1.000 1.000 5.00 1st Qu. 5.400 6.300 5.150 5.650 6.73 Median 7.000 7.500 6.850 7.500 7.80 Mean 6.816 7.402 6.618 7.046 7.73 3rd Qu. 8.300 8.600 8.600 8.800 8.75 Max. 10.000 10.000 10.000 10.000 10.00 NA's 6100.000 160719.000 7144.000 7101.000 50638.00
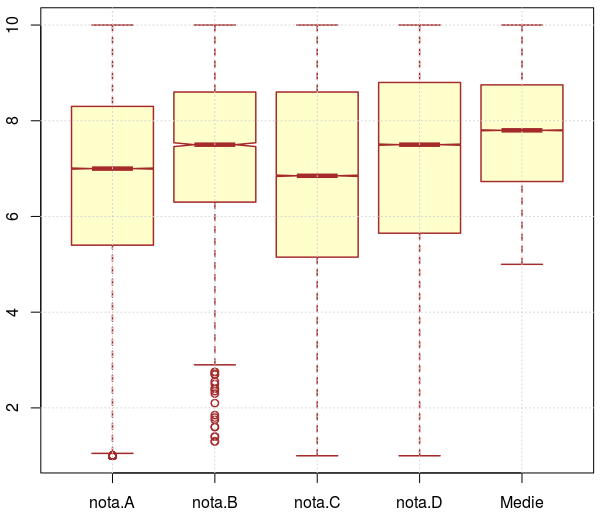
Corespunzător matricei redate, avem "boxplot"-ul alăturat mai sus (v. [2]; click-dreapta şi View Image pentru a mări imaginea), obţinut prin:
boxplot(bac5[c(19:22, 25)], notch=TRUE, col="#FFFFCC", border="brown", lwd=1.5)
În coloana 'nota.B' avem 160719 valori 'NA' (note neatribuite); aceasta înseamnă că proba de "Limba maternă" a fost susţinută de nrow(bac5) - 160719 = 8220 candidaţi şi fiindcă proporţia acestora (4.87% din numărul total de candidaţi) este aşa de mică, nu ne vom ocupa aici separat, de această categorie.
Ne interesează repartiţia notelor (şi mediilor) pe intervalele obişnuite [1, 5), [5, 6), etc., vizând toţi candidaţii, sau eventual numai o parte a acestora (satisfăcând un anumit criteriu - de exemplu să fie din acelaşi judeţ, sau să fie de acelaşi sex, din aceeaşi promoţie, etc.). Vom constitui o funcţie numită "pergaps()", care să ne obţină procentele de candidaţi pe fiecare interval de medii ("gap"), pentru un subset din "bac5" furnizat ca argument.
Apar două probleme mai deosebite: valorile NA (ignorate de majoritatea funcţiilor statistice) sunt în număr diferit pe coloanele de note, încât avem de văzut cum putem obţine - într-o formulare unitară - numărul de candidaţi faţă de care vrem să obţinem procentele corespunzătoare intervalelor de medii (am folosit aici experienţa de prin [2] - vezi funcţia classify()); a doua problemă provine din faptul că pe coloana Medie nu avem valori din intervalul [1, 5) (metodologia închipuită pentru bacalaureat prevede calculul mediei numai în cazul când la toate probele s-a obţinut cel puţin 5) - ceea ce înseamnă că la clasificarea notelor pe intervale trebuie (neavând la îndemână o soluţie unitară) să tratăm separat cazul coloanelor de note (a 19-a, a 21-a şi a 22-a coloană) şi respectiv, cazul coloanei 25 (cea de "Medie").
pergaps <- function(set_bac, materna=FALSE) { # browser() # `set_bac`: subset din "bac5"; `materna`: include sau nu, notele din "Limba maternă" # Eroare ("no rows to aggregate") dacă o coloană de note din `set_bac` conţine numai `NA` cols <- c(19:22, 25) # indecşii coloanelor de note la probele A-D şi coloanei 'Medie' if(!materna) cols <- cols[-2] # exclude eventual, coloana notelor probei B ncl <- length(cols) sdf <- subset(set_bac, select=cols) # în "sdf" coloanele de note au rangurile 1..ncl proc <- data.frame(gap = c("[1,5)","[5,6)","[6,7)","[7,8)","[8,9)","[9,10]")) # în "proc" vom adăuga coloane cu procentele pe probe şi pe intervalele din "gap" breaks = c(1, 5:9, 10.01) # limitele standard ale intervalelor de medii for(k in 2:ncl) { lim <- cut(sdf[, k-1], breaks=breaks, right=FALSE) # clasifică notele proc[k] <- aggregate(sdf[, k-1] ~ lim, sdf, length)[2] # contorizează } # pentru coloana "Medie", exclude intervalul "[1, 5)" (s-au înscris numai mediile ≥ 5) m5 <- aggregate(sdf[, ncl] ~ cut(sdf[, ncl], breaks=breaks[-1], right=FALSE), sdf, length)[2] # contorizează pe intervalele rămase proc[ncl+1] <- c(0, m5[[1]]) # anexează 0 - elevi cu "Medie" < 5 names(proc)[2:(ncl+1)] <- names(bac5)[cols] # redenumeşte coloanele din 'proc' nelevi <- lapply(proc[2:(ncl+1)], sum) # numărul total de elevi, pe fiecare coloană proc[2:(ncl+1)] <- round(proc[2:(ncl+1)]/nelevi, 4)*100 # procent elevi pe interval list(proc, nelevi) # procentul de elevi pe intervale şi probe, total elevi pe probă }
Punerea la punct a acestei funcţii a fost un bun prilej de a clarifica vreo două aspecte "simple" (de limbaj R); a trebuit să folosesc funcţia browser(), pentru a urmări pas cu pas execuţia - am inserat "browser()" pe prima linie din corpul funcţiei şi am lansat pergaps(bac5):
Browse[2]> n # "next" - execută următoarea linie din corpul funcţiei debug at #17: proc[ncl + 1] <- c(0, m5[[1]]) # dar iniţial, pusesem GREŞIT m5[1] Browse[2]> m5[1] # m5 este o structură "data.frame", cu o singură coloană sdf[, ncl] 1 9981 # 9981 medii în intervalul [5, 6) 2 26059 # în intervalul [6, 7) 3 28731 # în intervalul [7, 8) 4 31515 # în intervalul [8, 9) 5 22015 # în intervalul [9, 10] Browse[2]> str(m5[1]) 'data.frame': 5 obs. of 1 variable: # COLOANA DE "data.frame" ESTE TOT "data.frame"! $ sdf[, ncl]: int 9981 26059 28731 31515 22015 Browse[2]> str(m5[[1]]) # m5[[1]] este VECTORul pe care-l voiam aici int [1:5] 9981 26059 28731 31515 22015
Secvenţa redată mai sus lămureşte distincţia dintre operatorii "[" şi "[["; făcând o analogie (reţinută de pe undeva) - cu "[ ]" poţi selecta unul sau mai multe vagoane ale unei garnituri de tren, în timp ce prin "[[ ]]" poţi obţine conţinutul unui anumit vagon. Am avut nevoie de cele 5 valori din structura de date "m5" (deci de m5[[1]]), pe care le-am completat cu 0 (numărul mediilor din intervalul [1, 5)), înscriind vectorul rezultat (cu 6 valori) în structura de date "proc" (în urma execuţiei liniei 17 din corpul funcţiei).
Al doilea aspect ţine de operatorul ":". Am fost neinspirat să folosesc repetat expresia "ncl + 1" (în penultimele patru linii din blocul funcţiei) - în loc de a considera o variabilă suplimentară (ncl1 <- ncl + 1; names(proc)[2:ncl1] ..., etc.) - şi iniţial am folosit "names(proc)[2 : ncl + 1]", ceea ce este greşit: ":" are prioritatea mai mare decât "+", încât de exemplu expresia "k=3; 1:k+1" va conduce la "2,3,4" şi nu la "1,2,3,4" (pentru care trebuiau paranteze "1: (k+1)").
Exemplificăm "pergaps()", comparând rezultatele a două categorii de elevi - cei care au susţinut "proba D" la "Informatică" (setul numit mai jos "matinf1") şi cei care au susţinut-o la "Biologie" sau "Anatomie" (setul "matinf2"), din rândul celor de la profilul "matematică-informatică":
matinf.1 <- subset(bac5, proba.C=="Matematică MATE-INFO" & startsWith(as.character(proba.D), "Infor")) pergaps(matinf.1) [[1]] # procente, pe intervale de medii [[2]] # total elevi gap nota.A nota.C nota.D Medie nota.A nota.C nota.D Medie 1 [1,5) 0.93 2.14 2.38 0.00 7211 7208 7212 6873 2 [5,6) 6.57 6.09 8.50 2.28 3 [6,7) 10.94 7.45 11.12 9.69 4 [7,8) 20.21 11.08 15.06 18.07 5 [8,9) 33.01 17.65 21.59 31.50 6 [9,10] 28.35 55.59 41.35 38.45 matinf.2 <- subset(bac5, proba.C=="Matematică MATE-INFO" & (startsWith(as.character(proba.D), "Biol") | startsWith(as.character(proba.D), "Anat"))) pergaps(matinf.2) [[1]] # procente, pe intervale de medii [[2]] # total elevi gap nota.A nota.C nota.D Medie nota.A nota.C nota.D Medie 1 [1,5) 4.51 14.94 8.24 0.00 17847 17739 17730 14269 2 [5,6) 15.61 18.50 11.21 6.69 3 [6,7) 15.49 12.73 13.25 18.14 4 [7,8) 19.16 14.63 16.07 22.50 5 [8,9) 25.79 16.81 21.46 29.39 6 [9,10] 19.44 22.39 29.77 23.29
Rezultatele celor care au susţinut proba D la "informatică" sunt clar mai bune decât ale celor care au susţinut-o la "biologie" sau "anatomie" (ignorând faptul că aceştia din urmă sunt de peste două ori mai mulţi): proporţia notelor între 8 şi 10 (rândurile 5 şi 6 din matricele de mai sus) este cu 16% mai mare la proba A, cu 34% mai mare la proba C şi cu 12% mai mare la proba D.
Lucrurile devin şi mai clare prin intermediul unui grafic, asociat matricelor de mai sus:
as.matrix(mtif1[-1]) -> mtif1.m # 'mtf1' este prima matrice (mtf1 <- pergaps(matinf1)[[1]]) dimnames(mtif1.m)[1] <- mtif1[1] # coloana 'gap' va denumi liniile noii matrice as.matrix(mtif2[-1]) -> mtif2.m # (mtf2 <- pergaps(matinf2)[[1]]) dimnames(mtif2.m)[1] <- mtif2[1] op <- par(mfrow = c(1, 2), # fereastra grafică va avea o linie şi două coloane font.main = 1, # text obişnuit (nu "bold", nici "italic") pentru titluri mar = c(5, 4, 4, 0.5)) # margine-dreapta de 0.5 rânduri, pentru prima coloană barplot(mtif1.m, # bare pe probe, pentru fiecare interval "gap" beside = TRUE, col = palette()[1:6], # coloane alăturate, colorate distinct ylim = c(0, 60), # procentele fiind între 0 şi 55.59 main="proba D: informatică", ylab="procente") grid(NA, NULL) # trasează numai linii orizontale, la valorile înscrise pe axa verticală par(mar=c(5, 0, 4, 2)) # fără margine-stânga, pentru graficul din a doua coloană barplot(mtif2.m, beside=TRUE, col=palette()[1:6], ylim=c(0, 60), axes = FALSE, # elimină axa verticală legend.text = TRUE, # adaugă o legendă, în dreapta sus args.legend = list(x="topright", cex=0.75), main = "proba D: biologie sau anatomie") # titlul graficului din a II-a coloană grid(NA, NULL) mtext("profilul 'Informatică-Matematică'", side=3, line=-1.1, outer=TRUE, cex=1.2) par(op) # reconstituie valorile implicite pentru parametrii grafici
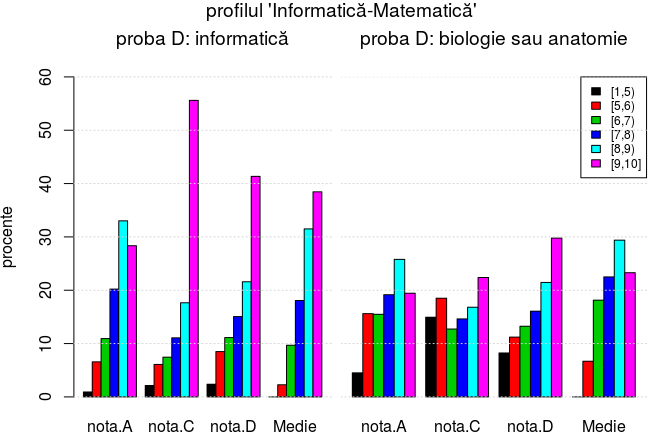
Probabil că acest grafic (sau ceva similar) se putea obţine mai simplu (şi fără a repeta comenzi, precum în secvenţa de mai sus) - dar a fost un bun prilej de a puncta elementele standard cele mai obişnuite în R, pentru formularea graficelor statistice.
Nu mai dăm aici alte exemplificări pentru funcţia "pergaps()", dar precizăm că la fel ca în cazul prezentat mai sus, putem compara subsetul celor care au susţinut proba C la "Matematică-TEHN", cu subsetul celor care au susţinut-o la "Istorie" şi putem obţine matricea procentelor pe intervale de medii pentru cei care au susţinut proba de "Limba maternă", sau pentru cei de sex "M" (versus "F"), sau pentru cei din mediul "Urban" (versus "Rural"), sau pentru cei dintr-un acelaşi judeţ, etc.
vezi Cărţile mele (de programare)