Imaginarea în MetaPost a elipselor tangente în O axei Ox
[1] O familie de elipse tangente în $\mathsf{O}$
la $\mathsf{O}x$
[2] Ecuaţiile elipselor tangente unei drepte într-un acelaşi punct
Să vedem cum ar fi să obţinem imaginea din "ellfam1.png" (v. [1]) folosind MetaPost (nu R, ca în [1] şi [2]); avem de confruntat maniere diferite de programare şi unele formate de imagine.
Dar întâi semnalăm o greşeală instructivă: în [1] am "formatat" însuşi titlul folosind MathJax, ceea ce nu-i tocmai potrivit: în cazul nostru, titlul articolului este şi conţinut al elementului <title> din secţiunea <head> a fişierului HTML respectiv; prin urmare, browser-ul va afişa titlul în bara de titlu a ferestrei în care va deschide articolul, dar înainte de a şti cumva (sau a lua în seamă) şi MathJax (astfel că titlul rămâne "neformatat"):
Pentru programul în R, a trebuit să folosim în mod explicit ecuaţiile şi formulele de calcul stabilite în [2]; în MP (MetaPost) putem ocoli explicitarea ecuaţiilor, având diverse posibilităţi de a descrie figurile.
În [2] (şi apoi, în [1]) am plecat de la ecuaţia elipsei raportate la axele proprii, am calculat unghiul cu care trebuie rotită elipsa şi vectorul cu care trebuie apoi translatată (astfel încât să obţinem o elipsă tangentă în $\mathsf{O}$ la $\mathsf{O}x$) şi am plotat punctele $(x,y)$ care satisfac ecuaţia obţinută. În orice limbaj cu posibilităţi grafice (inclusiv în MP) putem exploata astfel, ecuaţia dată a graficului.
Dar în MP dispunem de unele contururi predefinite, de o serie de transformări şi de posibilităţi pentru depistarea automată de puncte şi direcţii. Putem pleca de la p = fullcircle, care aproximează (dar suficient de bine) cercul de centru $\mathsf{O}$ şi diametru 1bp (=1/72inch); scalând pe orizontală şi pe verticală, prin p = fullcircle xscaled 2a yscaled 2b, obţinem o elipsă de semiaxe a şi b pe care o rotim cu g grade: w = p rotated g. Aflăm punctul "cel mai de sus" (opus lui $\mathsf{T}$ din [2]) al elipsei rotite w, prin T = directionpoint left of w (identificând punctul conturului w în care tangenta este orizontală şi orientată spre stânga); în final, translatăm conturul w încât centrul său să fie acum T şi eventual, plotăm: draw w shifted T - rezultând (fără a implica ecuaţii explicite) o elipsă tangentă în $\mathsf{O}$ axei $\mathsf{O}x$.
Conturul fullcircle conţine de fapt 8 puncte, anume cele aflate pe cercul unitar care sunt distanţate între ele cu câte 45°, începând de la "ora 3", în sens antiorar; interpolând prin curbe Bézier între primele trei puncte, rezultă sfertul de cerc din primul cadran, iar acesta este apoi completat la întregul cerc prin simetrie faţă de axe. Am putea obţine focarul din dreapta originii al elipsei p ca intersecţie a cercului centrat în punctul 2 de rază a cu semiaxa pozitivă Ox: q = fullcircle scaled 2a shifted(point 2 of p); f = q intersectionpoint (O -- 2a*right). Dar desigur că este mai simplu să folosim direct formula care ne dă abscisa focarului, $\sqrt{a^2-b^2}$, simbolizată în MP prin a +-+ b.
Deasemenea, folosim direct şi expresia obţinută în [1] $\mathrm{arctg}\sqrt{\frac{b}{a}}$ pentru unghiul cu care trebuie rotită elipsa de bază ca să obţinem acele elipse tangente în $\mathsf{O}$ la $\mathsf{O}x$ care au focarele situate pe o anumită cardioidă şi centrele pe un anumit arc de parabolă (semiaxa mare $a$ fiind constantă, iar semiaxele mici fiind date de $b=4at(1-t),\,t\in[0,\frac{1}{2}]$; v. [1]).
Putem formula programul final "ellipse.mp" astfel:
outputformat := "png"; %% pentru imagine în format PNG outputformatoptions := "format=rgba antialias=good"; outputtemplate := "%j-%c.png"; % şablonul numelui fişierului asociat figurii %% outputtemplate := "%j-%c.mps"; %% pentru imagine EPS (şi pentru 'epstopdf') numeric i; % pentru indexarea punctelor i := 0; pair F[], G[], C[]; % focarele şi centrele elipselor %% elipsa de semiaxe a, b rotită cu g grade şi translatată deasupra axei Ox def ellipse(expr a, b, g) = image( path p, w; pair T, f; p = fullcircle xscaled 2a yscaled 2b; w = p rotated g; T = directionpoint left of w; draw w shifted T withpen pencircle scaled 1; drawoptions(withpen pencircle scaled 3.5); C[i] = origin shifted T; draw C[i] withcolor blue; f = (a +-+ b, 0); % radical din (a^2-b^2) F[i] = f rotated g shifted T; G[i] = (-f) rotated g shifted T; draw F[i] withcolor red; draw G[i] withcolor red; draw F[i] -- G[i] withpen pencircle scaled 0.2 dashed evenly; i := i+1; drawoptions(); ) enddef; %% figură conţinând 16 elipse tangente în O axei Ox u = 36; % fixăm unitatea de măsură 36bp = 0.5 inch ax = 9/2u; % semiaxa mare este constantă beginfig(1); numeric bx, h; for t=1 upto 16: bx := 4*ax*(t/32)*(1-t/32); % semiaxele mici (v. [1]) h := angle((sqrt(ax), sqrt(bx))); % arctg(radical{b}/radical{a}) v. [1] draw ellipse(ax, bx, h); % elipsă tangentă în O la Ox endfor; path foc, goc, midd; % contururile focarelor şi centrelor foc = (2*ax,0) .. F[0] for i:=1 upto 15: .. F[i] endfor .. F[15]; goc = G[15] for i:=15 downto 0: .. G[i] endfor .. G[0]; midd = (ax,0) .. C[0] for i:=1 upto 15: .. C[i] endfor .. C[15]; draw (foc & goc) withcolor .6red; % '&' concatenează contururile draw midd withcolor .6blue; endfig; end % marchează încheierea definiţiilor de figuri
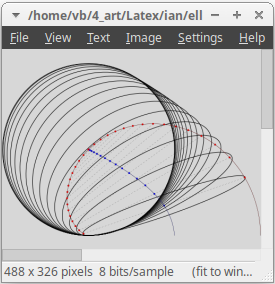Invocând (de pe linia de comandă) compilatorul de MP, prin mpost ellipse.mp, obţinem fişierul "ellipse-1.png" care poate fi vizualizat imediat (şi ca imagine, dar şi în hexazecimal, sau ca "text") din GNOME Commander (acţionând tasta F3).
Fişierul PNG obţinut astfel măsoară ≈65.5kB; menţionăm că fişierul PNG similar "ellfam1.png" obţinut în [1] prin R măsura ≈85.4kB şi figura numai 8 elipse (aici avem 16 elipse, care se disting însă din ce în ce mai greu odată cu apropierea centrului lor de punctul $(0,a)$).
În mod implicit, MP (ca întreg sistemul TeX) reprezintă numerele "in fixed point arithmetic", ca multipli întregi de $2^{-16}$; dar diferenţa de mărime evidenţiată mai sus nu rezultă din utilizarea unui model numeric diferit faţă de cel obişnuit: dacă am compila prin mpost -numbersystem=double ellipse.mp (forţând MP să adopte modelul numeric obişnuit), fişierul PNG rezultat are aproape aceeaşi dimensiune ca mai sus (chiar ceva mai mică, 65.3kB).
Formatul PNG este de ceva timp (încă) formatul standard pentru redarea imaginilor într-un browser, sau pe ecran (un defect încă important fiind acela că operaţia de "zoom" asupra imaginii, sau paginii care o conţine, face ca liniile să apară distorsionat). Pentru cazul imprimantelor este (încă) preferat format PS şi formatul PDF (cu avantajul că "zoom" nu va distorsiona imaginea, iar mărimea fişierului rezultat este sensibil mai mică decât în cazul formatului PNG).
Renunţând în programul de mai sus la primele trei linii (care aveau rostul de a forţa constituirea imaginii în format PNG), obţinem prin recompilarea programului imaginea respectivă în format EPS (care este formatul de ieşire implicit, pentru MP); dacă vom dori apoi să transformăm rezultatul în format PDF, atunci devine utilă setarea prealabilă outputtemplate := "%j-%c.mps"; (fără aceasta, numele fişierului va fi "ellipse.1" şi va trebui adăugată manual extensia ".mps", pentru ca un program ca epstopdf să-l poată converti la PDF).
Procedând astfel, rezultă fişierul "ellipse-1.mps", de numai ≈19.7kB, conţinând declaraţii şi instrucţiuni în limbajul PS; el poate fi vizualizat grafic de exemplu prin evince.
Invocând acum, de pe linia de comandă,
epstopdf ellipse-1.mps
obţinem fişierul în format PDF "ellipse-1.pdf", de numai ≈7.1kB. Desigur, pentru a reda aici acest fişier, am folosit un element HTML <iframe>; precizăm că pagina PDF respectivă se poate vedea mai bine în browser (Firefox) acţionând click-dreapta şi alegând "This Frame" şi apoi "Open Frame in New Tab"; acţionând butoanele "+" şi "-" se va putea constata că mărirea sau micşorarea imaginii nu afectează calitatea ei (liniile nu sunt distorsionate).
Ar fi de observat că cel mai firesc pentru imaginile în format PDF este încorporarea lor în documente LaTeX (şi nu în documente HTML, pentru care trebuie preferat un format ca PNG); cum am evidenţiat mai sus, browserele redau fişierele PDF ca pe nişte pagini cu totul speciale, cumva independent de contextul imaginilor PDF respective (încorporând anumite biblioteci pentru interpretarea specificaţiei PDF şi folosind tag-ul special <iframe>).
Să adăugăm în program, imediat înainte de endfig (schimbând şi beginfig(1); în beginfig(2);, pentru a nu suprascrie fişierele imagine obţinute anterior):
addto currentpicture also currentpicture reflectedabout(left, right);
addto currentpicture also currentpicture reflectedabout(down, up);
endfig;
Asigurăm astfel simetrizarea imaginii constituite anterior, faţă de axe; fişierul obţinut, "ellipse-2.pdf" are ≈17.6kB (revenind la format PNG, am obţine un fişier mult mai voluminos, de peste 200kB).
Dacă deschidem PDF-ul redat aici într-un nou TAB (setând "size" pe la 60%), avem o interpretare grafică a rezultatului de care ne-am ocupat în [1]: elipsele cu semiaxa mare $a$ constantă şi cu semiaxa mică $b=4at(1-t),\,t\in[0,\frac{1}{2}]$ au focarele pe două cardioide simetrice faţă de $\mathsf{O}y$ (cu nodul în $\mathsf{O}$ şi cu axa comună $\mathsf{O}x$) şi centrele pe două arce de parabolă simetrice faţă de $\mathsf{O}y$; contururile care corespund cardioidei şi respectiv parabolei au rezultat în program nu prin folosirea ecuaţiilor acestor curbe, ci folosind operatorul "..", destinat în MP pentru unirea a două puncte date printr-un arc de curbă Bézier.
vezi Cărţile mele (de programare)